（四）力学单位制 牛顿定律的简单应用
1．物理公式在确定物体量数量关系的同时，也确定了物理量的 关系。若公式是矢量式，则还同时确定了矢量 的关系。
2．在F=ma公式中，若有F选用“牛”则m 一定要选用 ，而a的单位必是 。只有如此才有F的数值与ma的数值相等。而F与a方向一致与单位的选定 。在国际单位制中可把“牛”这个复合单位写成基本单位的组合形式是 。若牛顿第二定律表达式中各量不选用国际单位制，则公式形应为F=Kma，显然公式中的K值由各物理量 决定的。
3．质量恒定的物体，在合外力改变的瞬间下列说法正确的是：（ ）
A．合外力方向不变而突增，速度方向不变突增
B．合外力方向不变而突增，加速度方向不变突增
C．若合外力大小不变方向时刻改变，加速度也大小不变方向时刻改变
D．合外力先突变加速度要逐渐地变
4．压强选用以Pa（帕）为单位，功率的单位W（瓦），分别写出它们在国际单位制中由基本单位而组合的形式：
Pa= W=
5．下列各国际单位中属于基本单位的是：（ ）
A．N（牛） B．m（米） C．W（瓦） D．kg（千克）
6．在相同力作用下，其加速度与质量成反比，数学关系式是： 或 ，对质量相同的物体，其加速度与合外力成正比的数学关系式是： 或 。将上述关系综合写成a∝ 式，将上述比例式写成等式形式是F= ，其中 时，k可等于1。
7．“动力学”是指物体的运动与受力关系的描述，解动力学题时将运动公式与牛顿定律综合应用，那末联系这两者的物理量是 。质点动力学往往有两类问题，一类是“已知受力求运动”即把物体受的所有力求合力再通过牛顿第二定律求出 再找到两个运动学量可求出另两个运动学量；另一类是“已知运动求受力”首先可找出 个运动学量，求出 再由牛顿第二定律求出合外力，根据已知力可求出未知力。
8．起重机钢索将质量m的物体由静止提升h(m)速度达到v(m·s－1)物体加速度a=
，钢索拉力T= N。这属于已知 求 类问题。
9．静止在水平面上的物体，质量为m在水平恒力F作用下前进t。设物体与水平面间滑动摩擦因数μ，物体运动加速度a= m/s2，物体通过的路程S= 。这属于已知 求 类问题。
10．在对物体进行受力分析时，确定某个力是否存在，可有两方面的根据。一是根据力产生的条件，二是根据物体已知力及运动状态来确定未知力，你能举出这两个方面的例子吗？（可在书本上或此练习上找）
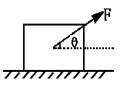
11．如图所示，质量为m=2kg的物体，在与水平方向成θ=37°的恒力F=10N作用下，沿水平面运动的加速度a=3m/s2，则物体与水平面间动摩擦因数μ= 。撤消F后物体速为5m/s物体运动加速度a＇= ，物体还能运动 m。
12．静止在光滑水平面上的物体，质量m=2kg，当它受到两个水平力的作用，F1=3N F2=5N，其运动加速度a=2m/s2，则a与F1的夹角为 度。
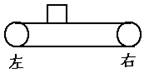13．在水平传送带上的物体质量m=3kg，设物体不会与带子滑动，如图所示。当物体与带子一起匀速向右运动时，物体受摩擦力为
，若带子向右以a=2m/s2的加速度匀加速运动时，物体受摩擦力大小
N，方向
。若带子以a=2m/s2的加速度向右匀减速运动时，物体受摩擦力大小
，方向
。
14．静止在水平面上的物体，在20N水平力拉动下前进5s,撤去水平力物体又前进15s而停止，物体受恒定阻力f= 。
15．静止在水平面上的物体，在水平恒力F拉动下前进S时撤去F，物体又前进2S才停止，则物体受恒定阻力f与F之比 。
16．沿斜角为θ的斜面匀速下滑的物体，当它受一个竖直向下的力作用时，下滑加速度为 m/s2。
17．物体沿斜面以加速度a匀加速下滑，当施于此物体一个竖直向下的恒力后，物体下滑加速度为a＇，则：（ ）
A．a＇=a B．a＇＞a C．a＇＜a D．不能确定a、a＇的大小关系
18．物体由h高处自由落下的时间为t，落地速度大小为v，若使物体沿光滑斜面，仍从h高处释放，设斜面的倾角为θ，则物体达斜面底端时速度大小为
v，物体运动时间为
t。
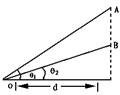
19．如图所示，两个光滑等底斜面AO和BO其倾角分别为θ1、θ2（θ1＞θ2）小球分别在两斜面的顶端释放达到底端经历的时间分别为t1与t2，讨论：t1与t2的大小关系。（sin2θ=2sinθ·cosθ）θ为何值时下滑时间最短。（分三种情况：（1）θ1、θ2都小于45°，（3）θ1＞45°，θ2＜45°）
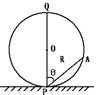
20.如图所示。在竖直圆内，半径为R、最高点Q、最低点P。有一光滑斜面一端在最低点P，另一端在圆周上A点。求：在A处释放一个小球（可视为质点）经多长时间t到达p点？
21．如图所示，光滑小盒中的球质量为m，被两根自由长和劲度k均相等的弹簧固定在盒的正中央。静止时两弹簧均为自由长，当水平方向具有加速度a 时，发现小球向右移动△L，则小球运动加速度a的大小及方向如何？若盒静止时两弹簧均比自由长长或均比自由长短，出现水平加速度a时小球仍向右移动△L,则a与上一问还一样吗？
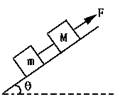22．在倾角为θ的斜面上，有两物体质量分别为m和M，两物用平行于斜面的轻绳连接在沿斜面向上的恒力F作用下加速向上运动，设斜面与物体间动摩擦因数均为μ，则连接绳中拉力多大？若μ=0，θ=0°时上述结论变化吗？若μ≠0，θ=0°时上述结论变化吗？若θ=90°时上述结论还正确吗？若两物与斜面间动摩擦因数不同，上述结论正确吗？
23．静止在光滑水平面上P点的物体，受向东大小为F 1的水平恒力作用t时间，速度大小为v1，立即撤去F1，改换向西的水平恒力大小为F2，作用t时间物体恰回到P点，此时速度大小为v2。以向东为正方向F1作用下的平均速度为
= ，F2作用下的平均速度为
=
，这两个平均速度的关系是
。
=
，
=
。
24．如图所示，水平传送带A、B端间距L=16m ，传送带以v=4m/s速度向右传送着，当轻轻将质量为m=1kg的物体放上A端（对地速度为零）则摩擦力对物体作用时间t1= s(设带物间动摩擦因数μ=0.2)物体由放上A端运动到B端共经历的时间t2=
s。
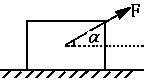25．如图所示，质量为m的物体在水平面上受与水平方向夹α角的力F作用，设物与水平面间动摩擦因数为μ。若物体沿水平面匀速运动时，F=
。若逐渐增大F，则地面对物体支持力变
，物体沿水平面运动的加速度变 。当物体沿水平面运动加速度最大时，=
，此时加速度a=
。
26．设某物体竖直下落时其阻力与速度的平方成正比（即f=kv2）物体由静止开始下落将怎样运动？若物体下落速度为5m/s时阻力恰为重力的
，物体运动的收尾速度多大？当物体下落速度为8m/s时，其瞬时加速度多大？
27．一轻质弹簧下面吊着物体静止时，弹簧伸长4cm（设不超过弹性限度）；当用此弹簧在水平面上水平匀速拉动该物体时，弹簧伸长1cm；若弹簧在水平面上水平拉动物体时弹簧伸长2cm，则该物体运动加速度a=
。
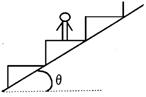
28．如图所示，自动扶梯的倾角为θ，质量为m的人站在扶梯上，若扶梯匀速运动时，人对梯的压力大小是 ，人受摩擦力大小是
。若扶梯正以加速度a向上启动时，人对梯压力大小 ，人受摩擦力大小为
。
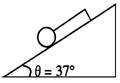
29．如图所示，倾角θ=37°的光滑斜劈上有被平行于斜面的线拉住的小球，球质量m=1kg，当斜劈以向左的加速度a左=
时，球受线拉力为零且不沿斜面上滑。当斜劈以向右的加速度a右=
时，球对斜面压力为零，且不飞起。若斜劈向左加速度为0.5g时，球对斜面压力大小为
N，球受线拉力大小 N。当斜劈以水平向右加速度为
g运动时，线中拉力大小 N，此时线与水平方向夹角为
度。
30．如图1所示，两物体质量均为m=1kg，两物之间用水平轻绳连接，B在水平恒力F作用下两物沿水平面匀速运动，设A物体与地面间动摩擦因数μA=0.1，B物与地面间动摩擦因数μ2=0.2 ，则F= N，连接绳中拉力T= N。若A、B间连接绳改为图2所示，θ=37°，水平拉力F仍为匀速运动时的数值，则T′= N，系统加速度a= m/s2。（两位有效数字）
31．水平恒力F在光滑水平面上推动质量为m的物体其加速度为a。当将另一质量为5kg的物体叠放在原物体上，设两物不发生滑动，右不改变F则两物共同加速度为
，若要维持原加速度a则增加水平推力6N。推力F=
N，m=
kg，a=
m/s2,两物体间相互作用的水平力
N。
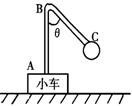32．如图所示，小车上连着弯成θ角的轻硬杆ABC，AB部分竖直，C端连有质量为m的小球。当小车匀速向左运动时，杆给球的力大小为
，方向
。为使杆给球的力沿杆BC的方向。车的水平加速度大小 ，方向 。若车水平加速向左且逐渐增大时，杆给球的力与竖直方向的夹角将逐渐
。
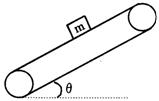33．质量m的物体放在倾角为θ的传送带上，设传送带分别如下运动时物体不在带上打滑。（1）带子匀速向上传动（2）带子匀速向下传送，（3）带子以加速度a向上传送，（4）带子以加速度a向下传送，分别讨论物体受静摩擦的大小及方向？
（五）超重和失重 牛顿运动定律的适用范围
1．下列哪种情况物体一定处于超重状态：（ ）
A．物体向上运动
B．物体向下运动
C．物体运动加速度向上
D．物体运动加速度向下
2．人静止在体重计上时，体重计的示数为G。当人突然下蹲一直到最低点静止的过程中人的重力怎样变 体重计的示数怎样变 。
3．站在升降机地板上的人，当升降机静止时重力大小为G，受地板支持力在小为N，人施于地板的压力大小为F。当升降机自由下落时，下列说法正确的是：（ ）
A．由于G=0则F和N 均为零
B．G＞N＞0，F=0
C．G不变，F=N=0
D．G=F＞0，N=0
4．如图所示，P、Q两物体叠放。不计空气阻力，向各方向抛出时设两物接触面仍水平，P的重力大小为G，P受Q支持力大小为N。则
A．竖向上抛出后，N＞G
B．平抛出后，G=0，N=0
C．竖直向下抛出后G＞N＞0
D．无论怎样抛出后都是G不变N=0
5．升降机的天花板上吊着弹簧秤，其下端吊着重20N的物体，当弹簧秤的示数为10N时，升降机的运动状态可能是：（ ）
A．正在匀速下降
B．不可能上升
C．以
的加速度匀减速长升
D．以加速度匀加速下降
6．一个运动员在匀速运动的升降机中最好成绩是举起600kg的杠铃。当升降机具有向上的加速度时，他的最好成绩是
kg；若升降机有向下的加速度时，他最好成绩是
kg。
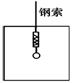7．如图钢索吊着箱子，箱子内有弹秤吊着重10N的小球。当弹簧秤的示数为10N时，钢索拉力为510N，若弹簧秤示数为7N时，钢索拉力 N。此时箱子正在
上升或正在
下降。
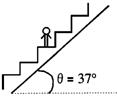8．如图所示，人站在倾角为θ=37°的自动扶梯上的水平活动台阶上。若质量为 m的人受到台阶水平向左的静摩擦大小为0.3mg，此时台阶对人的支持力N为
mg。扶梯的加速度a=
g，方向
。能判断出自动扶梯的运动方向吗
。
9．站在上图中自动扶梯的人，当发现自己对台阶的压力比重力增加
，可知：（ ）
A．扶梯一定在向上启动
B．人受台阶摩擦力一定向左
C．人受摩擦力大小为
mg
D．扶梯加速度大小为
g，且斜向上
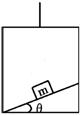10．如图所示，升降机地板上有倾角为θ的斜面，质量为m的物体总能静止在斜面上。升降机匀速运动时，物体受支持力为
，受摩擦力为
。若升降机以向上的加速度a运动着，物体受支持力为 ，物体受摩擦力为
。若升降机具有向下加速度为重力加速度的
时，物体受支持力为
，受摩擦力为
。
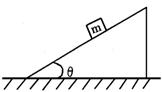11．如图所示，倾角为θ的斜劈，其斜面上静止着质量为m的物体，地面对斜劈的支持力为
，设斜劈质量为M。若物体沿斜面加速下滑时，其加速度大小为a，则地面对斜劈支持力为
，地对斜劈的静摩擦大小
方向
。
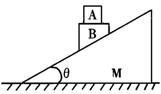12．如图所示，静止在水平粗糙地面上质量为M倾角为θ的斜劈，其斜面光滑。物体A、B叠放在光滑斜面上下滑（A、B不发生相对滑动）它们的质量分别为m1、m2，它们的接触面水平。则A对B的压力为
，A对B的静摩擦
；M对地压力为
，M对地的静摩擦
。
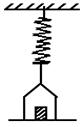13．如图所示，一根轻弹簧上端固定，下端挂一质量为m0的平盘，盘中有质量为m的物体。盘静止时，弹簧长度比自由长伸长L，今向下拉盘使弹簧再伸长△L（△L＜L）后停止。然后松手放开，设弹簧在弹性限度内，则刚松手时盘对物体支持力等于：（ ）
A．（1+
）mg
B．(1+)(m+m0)g
C．mg
D． (m+m0)g
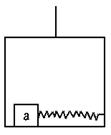14.如图所示，原来作匀速运动的升降机地板上，有一个被伸长弹簧拉住的，具有一定质量的物体a静止在地板上。后来发现a突然弹簧拉向右方，由此可判断升降机可能是：
（ ）
A．加速上升 B．减速上升
C．加速下降 D．减速下降
（四）
（1）单位 方向 （2）kg, m/s2，无关，kg·m·s－2,单位制 （3）BC
（4）kg·m－1·s－2, kg, m2, s－3 (5)BD
（6）
， a∝
。
，a∝
。 F=kma, m选kg单位，a选m/s2单位，则F单位是kg·m/s2即牛。 （7）加速度，加速度，三，加速度
（8）
，m(g+)，运动，受力 （9）（
） 
（），受力，运动
（10）略
（11）
（12）90
（13）0，6N，右， 6N， 左 （14）5N （15） （16）0 （17）B （18）1，
(19)
g·sinθ·t2,t=
,当θ=45°时t最短,θ1+θ2=90°时t相同
(20)
(21)
，向左，几种情况相同。
（22）F
,几种情况都是此规律，μ1≠μ2结论不成立（θ=90°除外）
（23）
向东，
向西，等值、反向，，
（24）2s, 5s
(25)
，小，大，
，g·ctgα
（26）加速度逐渐减小的加速运动最后以最大速度匀速运动， 10m/s, 0.36g
(27)
(28)mg, 0,
mg(1+
),ma·cosθ （29）
11.2, 20,30°
(30)3, 1, 1, 4N, 0.056 (31)3, 2.5, 1.2, 6
(32)mg, 竖直向上，tgθ·g，水平向左，增大
(33)(1)(2)均是沿带向上，大小为mgsinθ， （3）沿带向上，mgsinθ+ma (4）若a=gsinθ，f=0, 若a＜gsinθ，f沿斜面向上，mgsinθ－ma 若a＞gsinθ，f治带向下，ma－mgsinθ
(五)
（1）C （2）重力不变，先减小后增加，最后等于G （3）C （4）D （5）CD
（6）400， 1200 （7）357，减速，加速 （8）0.6，，斜向下，不能 (9)CD
（10）mgcosθ，mgsinθ, m (g+a) cosθ, m (g+a) sinθ, 
mgcosθ, mgsinθ
（11）(M+m) g, Mg+m (g－asinθ) , macosθ, 左
（12）m1gcos2θ, m1gsinθ·cosθ, Mg+ (m1+m2) gcos2θ, (m1+m2) gsinθ·cosθ
（13）A （14）BC