第一节 质点运动的基本概念巩固练习
1.关于速度与加速度的说法，错误的是（ ）
A.速度增大时，加速度不一定增大 B.速度减小时，加速度一定减小
C.速度改变量越大，加速度越大 D.加速度与速度的大小及方向无关
2.某物体以2 m/s2的加速度做匀加速直线运动，则该物体（ ）
A．任意1s的末速度都是该1s初速度的2倍
B．任意1s的末速度都比该1s初速度大2m/s
C．任意1s内的平均速度都比前1s内的平均速度大2m/s
D．任意1s的初速度都比前1s的末速度大2m/s
3.一短跑运动员在100m比赛中跑到50m时速度大小是9.5m/s，在10秒末到达终点时的速度大小为11.5m/s，这名运动员在百米赛程中的平均速度大小是( )
A.11.5m/s B.10.5m/s C.10m/s D.9.5m/s
4.参加汽车拉力赛的越野车，先以平均速度V1跑完全程的2／3，接着又以V2=40km／h的平均速度跑完剩下的1／3路程。已经测出在全程内的平均速度V=56km／h，那么V1应是( )
A.60km／h B.65km／h C.48km／h D.70km／h。
5.关于位移和路程，以下说法中正确的是( )
A.出租车按位移的大小收费
B.出租车按路程收费
C.在曲线运动中，同一运动过程的路程一定大于位移的大小
D.不管是直线运动还是曲线运动，同一运动过程的路程总不小于位移的大小
6.两列火车相向而行，第一列的速度大小为36km／h，第二列为54km／h。第一列火车上的乘客测出第二列火车从他旁边通过所用的时间为5s。以下结论正确的是( )
A.两列火车的长度之和为125m
B.第二列火车的长度是125m
C.第二列火车的长度是75m
D.由于第一列火车的长也未知，故无法求出第二列火车的长
7.将一小钢球竖直向上抛出，在它上升到最大高度18m时，又沿原路线落回到地面。则在此过程中，小钢球通过的路程是_________m,其位移等于________。
8.一火车由甲站以60km/h的平均速度开出10min后，一辆汽车去追赶这列火车，必须在15min内追上这列火车，那么汽车的平均速度不得少于__ __km/h。
9．为使火药立即爆炸，应对其点燃。为安全往往是先点燃导火索，在导火索慢慢燃烧时点火员可跑到安全地带，导火索燃尽而点燃火药爆炸。设导火索长度为L，安全距离为S，则点火员的平均速度与导火索燃烧的平均速度之比为 。
10．某测量员是这样利用回声测距离的：他站在两平行峭壁间某一位置鸣枪，经过1.00s第一次听到回声，又经过0.50s再次听到回声，已知声速为340m/s，则两峭壁间的距离为
m。
11．天文观测表明，几乎所有远处的恒星（或星系）都在以各自的速度背离我们而运动，离我们越远的星体，背离我们运动的速度（称为退行速度）越大；也就是说，宇宙在膨胀．不同星体的退行速度v和它们离我们的距离r成正比，即：v＝Hr，式中H为一常量，称为哈勃常数，已由天文观察测定．为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的．假设大爆炸后各星体即以不同的速度向外匀速运动，并设想我们就位于其中心，则速度越大的星体现在离我们越远．这一结果与上述天文观测一致．
由上述理论和天文观测结果，可估算宇宙年龄Ｔ，其计算式为Ｔ＝＿＿＿＿．根据近期观测，哈勃常数 H＝3×10－2 米／秒·光年，其中光年是光在一年中行进的距离，由此估算宇宙的年龄约为＿＿＿＿年．
12．一支300m长的队伍，以1m/s的速度行军，通讯员从队尾以3m/s的速度赶到队首，并立即以原速率返回队尾，求通讯员的位移和路程各是多少？
13．坐在司机旁的乘客，发现前面约200m处有一拖拉机正向前行驶，这时它开始用手表计时，30s后汽车追上了拖拉机。从汽车速度表上看，乘客看到的车速一直是45km/h，如果拖拉机都是匀速行驶的。求拖拉机的速度多大？
14．火车从甲站到乙站正常行驶速度是60km/h，有一次火车从甲站开出，由于迟开了5分钟，司机把速度提高到72km/h，才刚好正点到达乙站。求：
（1）甲、乙两站间的距离
（2）火车从甲站到乙站正常行驶的时间
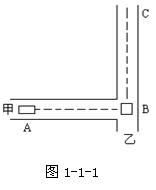
15．如图1-1-1所示，公路AB⊥BC，且已知AB=100米，车甲从A以8米/秒的速度沿AB行驶，车乙同时从B以6米/秒的速度沿BC行驶，两车相距的最近距离是多少？
第二节 匀变速直线运动的规律（Ⅰ）巩固练习
1．甲、乙两车从同一地点出发向同一方向沿直线运动，甲由静止开始以5m/s2的加速度作匀加速直线运动，2秒后乙以6m/s2的加速度由静止开始作匀加速直线运动，则在乙追上甲之前，两车间的最大距离是( )
A．15m B．10m C．24m D．60m
2．由静止开始做匀加速直线运动的汽车，头1s内通过0.4m路程，则（ ）
A．第1秒末的速度为0.8m/s B．加速度为0.8m/s2
C．第2s内通过的路程为1.2m D．头2s内通过的路程为1.2m
3．一物体做匀变速直线运动，某时刻速度大小为4m/s，1S后速度大小为10m/s，在这1S内该物体的（ ）
A．位移的大小可能小于4m B．位移的大小可能大于10m
C．加速度的大小可能小于4m/s2 D．加速度的大小可能大于10m/s2
4．质点在a、b两点之间做匀加速直线运动，加速度方向与初速度方向相同．当在a点初速度为v时，从a点到b点所用的时间为t；当在a点初速度为2v时，而保持其他量不变，从a点到b点所用的时间为tˊ，则（ ）
A．tˊ>t/2 B．tˊ=t/2 C．tˊ<t/2 D．tˊ=t
5．有一个物体开始时静止在O点，先使它向东作匀加速直线运动，经过5秒钟，使它的加速度方向立即改为向西，加速度的大小不改变，再经过5秒钟，又使它加速度方向改为向东，但加速度大小不改变，如此重复共历时20秒，则这段时间内（ ）
A．物体运动方向时而向东时而向西 B．物体最后静止在O点
C．物体运动时快时慢，一直向东运动 D．物体速度一直在增大
6．汽车以20m/s的速度做匀速直线运动，刹车后的加速度为5m/s2，那么刹车后2S与刹车后6S汽车通过的位移之比为（ ）
A．1∶1 B．3∶1 C．3∶4 D．4∶3
7．在水平直线轨道上行驶的列车，从制动开始起位移与时间的关系式为s=20t–0.25t2(m)，式中t的单位为s，则列车刚开始制动时的速度为 m/s，列车制动加速度大小为
m/s2，列车制动过程经历的时间是 s，制动全过程经过的路程是 m。
8．质点从静止开始做匀加速直线运动，经5s后速度达到10m/s，然后匀速运动了20s，接着经2s匀减速运动后静止，则质点在加速阶段的加速度是＿＿＿＿m/s2，在第26s末的速度大小是＿＿＿＿m/s．
9．汽车由静止开始以大小为a1＝2m/s2的加速度作匀加速直线运动，紧接着又做加速度a2＝4m/s2的匀减速直线运动直到静止，若运动的总时间为9S，则汽车运动的总位移为多少？汽车运动过程中的最大速度为多少？
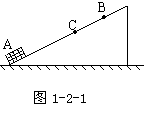10．如图1-2-1所示的光滑斜面上，一物体以4m/s的初速度由斜面底端的A点匀减速滑上斜面，途经C和B，C为AB中点，已知vA∶vC= 4∶3，从C点到B点历时（
）S，试求：
（1）到达B点的速度？
（2）AB长度？
11．在正常情况下，火车以54km/h作匀速直线运动。火车在经过某小站时要作短暂停留。火车将要到小站时以－0.5m/s2的加速度作匀减速直线运动，停留2分钟后，又以0.3m/s2的加速度驶出小站直到恢复原来的速度，求：火车因停靠小站而延误的时间。
12．一辆具有良好制动器的汽车，当它以v１=72km/h的速度沿平直公路匀速行驶时，司机突然发现前方有障碍物而紧急制动，汽车通过s１=50ｍ停下。如果汽车以v２=36km/h的速度行驶，则汽车通过s2=16m停下。假设司机的反应时间（司机从看见障碍物到制动器开始起作用的一段时间）相同，制动器起作用后汽车的加速度相同，求：司机的反应时间和汽车的加速度。
13．羚羊从静止开始奔跑，经过50m的距离能加速到最大速度25m/s，并能维持一段较长的时间。猎豹从静止开始奔跑，经过60m的距离能加速到最大速度30m/s，以后只能维持这个速度4.0s。设猎豹距离羚羊x m开始发起攻击，羚羊则在猎豹开始攻击后1.0s才开始奔跑，假定羚羊和猎豹在加速阶段分别做匀加速运动，且均沿同一直线运动。求：
（1）猎豹要在最大速度减小前追到羚羊，x值应在什么范围内？
（2）猎豹要在其加速阶段追上羚羊，x值应在什么范围内？
14．火车正以速率v1向前行驶,司机突然发现正前方同一轨道上距离为s处有另一火车,正以较小的速率v2沿同方向做匀速运动,于是司机立刻使火车做匀减速运动,要使两列火车不相撞,加速度a的大小至少应是多少?
15．列车沿轨道直线由A地驶向B地,A、B相距为s，列车从A地由静止出发做匀加速直线运动,加速度大小为a1，接着做匀减速直线运动，加速度大小为a2，到达B时恰好静止，求列车由A到达B的时间t。
第三节 匀变速直线运动的规律（Ⅱ）巩固练习
1．一质点做匀加速直线运动，第三秒内的位移2m，第四秒内的位移是2.5m，那么以下说法中正确的是( )
A．这两秒内平均速度是2.25m/s
B．第三秒末即时速度是2.25m/s
C．质点的加速度是0.125m/s2
D．质点的加速度是0.5m/s2
2．一个物体做匀变速直线运动,若运动的时间之比为t1：t2：t3：…=1：2：3：…,下面说法中正确的是（ ）
A．相应的运动距离之比一定是s1：s2：s3：…=1：4：9： …
B．相邻的相同时间内的位移之比一定是s1：s2：s3：…=1：3：5： …
C．相邻的相同时间内位移之差值一定是△s=aT2,其中T为相同的时间间隔.
D．以上说法正确都是不正确的
3．火车在平直轨道上作匀加速直线运动。车头通过某路标时的速度为υ1，车尾通过该路标的速度为υ2，则火车的中点通过该路标的速度为（ ）
A．
B．
C．
D．
4．物体从光滑斜面顶端由静止开始下滑、经过1秒到达斜面中点。那么物体下滑的总时间是（ ）
A．2秒 B．
秒
C．4秒 D．/2秒
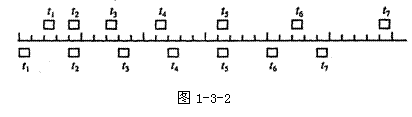
5．两木块自左向右运动，现用高速摄影机在同一底片上多次曝光，记录下木块每次曝光时的位置；如图1-3-2所示，连续两次曝光的时间间隔是相等的，由图可知（ ）
A．在时刻t2以及时刻t5两木块速度相同
B．在时刻t3两木块速度相同
C．在时刻t3和时刻t4之间某瞬时两木块速度相同
D．在时刻t4和时刻t5之间某瞬时两木块速度相同
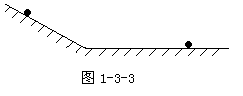6．如图1-3-3所示，小钢球从斜面上一点开始，沿斜面做初速为零的匀加速直线运动，经过2S运动到斜面底端时速度为4m／s。然后沿水平面做匀减速直线运动，又运动了6s才停下来。则小球运动的总路程应是（ ）
A.16m B.32m C.20m D.24m
7．一颗子弹沿水平方向射来，恰穿透三块相同的木板，设子弹穿过木板时的加速度恒定，则子弹穿过三块木板所用的时间之比为________。
8．一个做匀变速直线运动的物体连续通过s1、s2两段位移，所用时间均为t，则物体在经过这两段位移的中间时刻的即时速度为______。
9．从静止开始做匀加速直线运动的物体，第1个5s内的位移是10m，第1个10s内的位移为_____m，第3个10s内的位移为_____m。
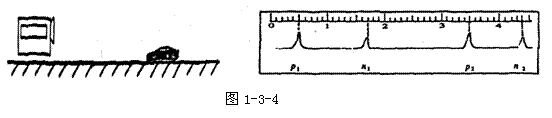10．如图1-3-4所示，左图是在高速公路上用超声波测速仪测量车速的示意图，测速仪发出并接收超声波脉冲信号，根据发出和接收到的信号间的时间差，测出被测物体的速度，右图中p1 、p2是测速仪发出的超声波信号，n1、n2分别是p1、p2由汽车反射回来的信号．设测速仪匀速扫描，p1、p2之间的时间间隔为Δt＝1.0s，超声波在空气中传播的速度是v＝340m/s，若汽车是匀速行驶的，则根据右图可知，汽车在接收到p1、p2两个信号之间的时间内前进的距离是＿＿＿＿m，汽车的速度是＿＿＿＿m/s。
11．滑雪运动员由一斜坡某处从静止开始滑下，滑到坡底又在水平面上继续运动到某处恰停下来，滑行总路程为S，在坡上运动时间t1，在水平面上运动时间t2。求：
（1）他滑行中的最大速率
（2）在斜坡上与水平面上运动加速度大小之比
（3）在斜坡上滑行与水平面上滑行距离之比
12．一质点做匀加速直线运动，其加速度为ａ，某时刻通过Ａ点，经时间Ｔ通过Ｂ点，发生的位移为ｓ1，再经过时间Ｔ通过Ｃ点，又经过第三个时间Ｔ通过Ｄ点，在第三个时间Ｔ内发生的位移为ｓ3，试利用匀变速直线运动公式证明：ａ＝（ｓ3－ｓ1）／2Ｔ2．
13．物体从O点由静止开始作匀加速直线运动，A、B、C、D为轨迹上的依次四点，测得AB=2m,BC=3m,CD=4m,若物体从A到B用时1s，求OA间距、物体的加速度、物体到B点时的速度。
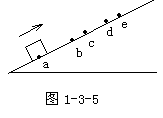14．如图1-3-5所示，物体沿斜面向上运动，依次经a、b、c、d到达最高点e，已知ab=bd=6m，bc=1m，小球从a到c和从c到d所用的时间都是2s，求：
（1）物体经过b、c两点时的速度各为多少？
（2）d和e之间的距离及从d到e所用时间为多少？
15．一辆汽车在十字路口遇红灯，当绿灯亮时汽车以4米/秒2的加速度开始行驶，恰在此时，一辆摩托车以10米/秒的速度匀速驶来与汽车同向行驶，汽车在后追摩托车，求：
(1)汽车从路口开始加速起，在追上摩托车之前两车相距的最大距离是多少？
(2)汽车经过多少时间能追上摩托车?此时汽车的速度是多大?
第四节 自由落体运动巩固练习
1．一个作自由落体运动的物体（ ）
A．经相同的时间速度变化相同
B．经相同距离速度变化相同
C．速度变化对时间是均匀的
D．速度变化对位移是均匀的
2．一个物体做自由落体运动，经过1秒钟下落的高度恰是它开始下落时的高度的三分之一，g取9.8m/s2，则物体开始下落时的高度为( )
A.9.8mm B.14.7m C.19.6m D.4.9m
3．甲、乙两物质量分别为m1、m2，它们分别从h1、h2高处同时释放，不计空气阻力，在它们均未落地前，以下正确说法是（ ）
A．它们运动加速度相同
B．由于不知质量和高度谁大，故不知哪个加速度大
C．它们在同一时刻的速度相同
D．它们相对静止，即下落的时候间距不变
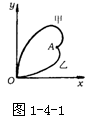4．甲、乙两小分队进行代号为“猎狐”的军事演习，指挥部通过现代通信设备，在荧屏上观察到小分队的行军路线如图1-4-1所示，小分队同时由同地O点出发，最后同时捕“狐”于A点，下列说法正确的有( )
A．小分队行军路程S甲＞S乙
B．小分队平均速度v甲=v乙
C．y—x图线是速度（v）—时间（t）图象
D．y—x图象是位移（S）—时间（t）图象
5．如图1-4-2所示，表示物体作匀速直线运动的图象是（ ）
 |
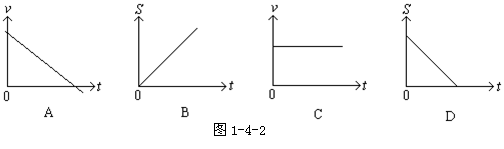6.自由下落的物体，自起点开始依次下落三段相等位移所用时间的比是（ ）
A.1∶3∶5 B.1∶4∶9
C.1∶
∶
D.1∶（
）∶ （
）
7.一观察者发现，每隔一定时间有一滴水自8 ｍ高的屋檐落下，而且看到第五滴水刚
要离开屋檐时，第一滴水正好落到地面.那么，这时第2滴水离地的高度是（ ）
A.2 ｍ B.2.5 m C.2.9 m D.3.5 m
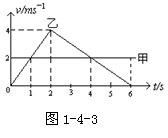8．在同一地点，甲、乙两个物体沿同一方向作直线运动的速度一时间图象如图1-4-3所示，则（ ）
A．两物体相遇的时间是2S和6S
B．乙物体先在前运动2S，随后作向后运动
C．两个物体相距最远的时刻是1S末和4S末
D．4S后甲在乙前面
9．已知物体作自由落体运动，在落地的前一秒内下降35m。其落地速度大小为 m/s，它是从 m高处自由落下的。（g=10m/s2）
10.自由落体运动的物体，在相邻的两个两秒内位移的差为 m，由落下开始各相等时间内下落的高度比为 。（g=10m/s2）
11．有一铁链，悬其上端。若从悬点放开铁链，则铁链经过悬点下20米处所用时间恰好是1秒钟，求铁链长。（g取10m/s2）
12．一小钢球从A点自由下落，经过B点到达C点。已知它过B点的速度是它过C点时速度的2／3，BC间的距离为5m，试求AC间的距离。（g取10m/s2）
13．一矿井深45米，在井口每隔一定时间自由落下一个小球，当第7个小球从井口开始
下落时，第一个小球恰好落至井底，问：（g取10m/s2）
（1）相邻两个小球下落的时间间隔是多少？
（2）这时第3个小球和第5个小球相距多远？
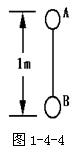
14．如图1-4-4所示，A、B两球用长1m的绳子相连，用手拿着A球时，B球距地h，释放A后不计空气阻力，两球落地时间差△t=0.2s，g取10m/s2，g取10m/s2，则h为多大？
15.一跳伞运动员从350 ｍ高空离开飞机跳伞降落，为了使落地时间快一些，开始时未打开伞而自由下落，降落一段距离后才张开伞，张开伞后以2 m/s2的加速度匀减速下落，到达地面时的速度为4 m/s.问跳伞运动员应在离地面多高时张开伞?(g=10 m/s２)
第一章 直线运动总结性测试
一、选择题（4分×10=40分）
1．一个运动员在百米赛跑中，测得他在50m处的速度是6m/s，16s末到终点时的速度是7.5m/s，则全程内的平均速度的大小是（ ）
A．6m/s B．6.25m/s C．6.75m/s D．7.5m/s
2．汽车在平直的公路上做加速度为0.5m/s2的匀加速运动，那么在任意1s内（ ）
A．汽车的末速度一定等于初速度的0.5倍
B．汽车的初速度一定比前1s内的末速度大0.5m/s
C．汽车的末速度比前1s内的初速度大0.5m/s
D．汽车的末速度一定比初速度大0.5m/s
3．关于物体的运动，下面说法中不可能的是（ ）
A．加速度在减小，速度在增加
B．加速度的方向始终变而速度不变
C．加速度和速度大小都在变化，加速度最大时速度最小，速度最大时加速度最小
D．加速度的方向不变而速度方向变化
4．如果运动物体有加速度，则该物体的速度大小和方向可能发生变化的是（ ）
A．速度方向、大小都不变
B．速度方向变化、大小不变
C．速度方向、大小都变
D．速度方向不变、大小变化
5．质点从静止开始作匀加速直线运动，从开始运动起，通过连续三段路程所经历的时间分别为1s、2s、3s，这三段路程之比是（ ）
A．1:2:3 B．1:3:5 C．12:22:32 D．13:23:33
6．一辆汽车以20m/s的速度沿平直公路匀速行驶，突然发现前方有障碍物，立即刹车，汽车以大小是5m/s2的加速度做匀减速直线运动，那么刹车后2s内与刹车后6s内汽车通过的位移之比为（ ）
A．1:1 B．3:4 C．3:1 D．4:3
7．作匀变速直线运动的物体先后经过A、B两点，在它们中间位置的速度为v1，在中间时刻的速度为v2，则（ ）
A．物体作加速运动时，v1>v2 B．物体作加速运动时，v2>v1
C．物体作减速运动时，v1>v2 D．物体作减速运动时，v2>v1
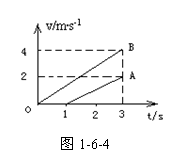8．A、B两质点的v－t图像如图1-6-4所示，设它们在同一条直线上运动，在t=3s时它们在中途相遇，由图可知（ ）
A．A比B先启程
B．A比B后启程
C．两质点启程前A在B前面4m
D．两质点启程前A在B后面2m
9．一辆汽车沿平直公路以速度v1行驶了2/3的路程，接着又以速度v2=20km/h行驶完其余1/3的路程，如果汽车对全程的平均速度为28km/h，那么汽车在前2/3路程上速度的大小是
A．25km/h B．34km/h C．35km/h D．38km/h （ ）
10．从某一高度相隔1s先后释放两个相同的小球甲和乙，不计空气阻力，它们在空中任一时刻（ ）
A．甲乙两球距离始终保持不变，甲乙两球速度之差保持不变
B．甲乙两球距离越来越大，甲乙两球速度之差也越来越大
C．甲乙两球距离越来越大，甲乙两球速度之差保持不变
D．甲乙两球距离越来越小，甲乙两球速度之差也越来越小
二、填空题（6分+6分+8分=20分）
11．客车以v1匀速前进，前方s0处货车以v2（小于v1）匀速前进，为避免相撞，客车立即刹车，则加速度的大小至少为 时才能避免相撞？
12．相距12km的公路两端，甲、乙两人同时出发相向而行，甲的速度为5km/h，乙的速度为3m/h，有一小犬以6km/h同时由甲向乙跑，遇到乙后回头向甲跑，如此往复，直到甲、乙相遇，则此过程中犬的路程为 km。
13．某质点从静止开始以加速度a1做匀加速直线运动，经t秒钟加速度大小立即变为a2，方向相反，再经t秒钟恰好回到原出发点，则a1、、a2的比值为 。
三、计算题（共90分）
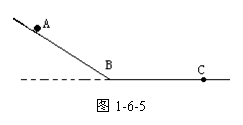14．（12分）如图1-6-5所示，物体由静止从A点沿斜面匀加速下滑，随后在水平面上作匀减速运动，最后停止于C点，已知AB=4m,BC=6m，整个运动历时10s，求物体沿AB和BC运动的加速度。
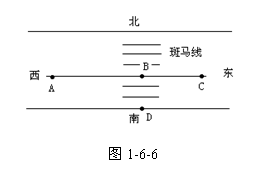15．（12分）如图1-6-6所示，在某市区，一辆小汽车在平直公路上向东匀速行驶，一位游客正由南向北从斑马线上横穿马路，司机发现前方有危险（游客在D处），经0.7s作出反应，紧急刹车，仍将正步行至B处的游客撞伤，汽车最终停在C处，为了解现场，警方派一警车以法定最高速度vm=14m/s，行驶在同一路段，在肇事汽车的起始制动点A紧急刹车，经14m后停下来，现测得AB=17.5m、BC=14m、BD=2.6m，问：（1）肇事汽车的初速度是多大？（2）游客横穿马路的速度是多大？
16．（12分）一辆轿车的最大速度为30m/s，要想从静止开始用4分钟追上前面1000m处以25m/s匀速同向行驶的货车，轿车至少要以多大的加速度起动？
17．（13分）一列火车做匀变速直线运动驶来，一人在火车旁观察火车的运动，发现相邻的两个10s内，列车从他跟前驶过8节车厢和6节车厢，每节车厢长8m，求：
（1）火车的加速度
（2）人开始观察时火车的速度大小。
18．（13分）物体原来静止在光滑的水平面上，现在奇数秒内由于受恒力作用作2m/s2的匀加速直线运动，偶数秒内作匀速运动，经多长时间物体的位移达到40.25m。
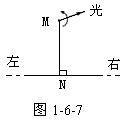
19．（14分）如图1-6-7所示，一辆实验小车可沿水平地面（图中纸面）上的长直轨道匀速向右运动，有一台发出细光束激光器装在上转台M上，到轨道的距离MN为d=10m，如图所示，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60s，光束转动方向如图中箭头所示，当光束与MN的夹角为45o时，光束正好射到小车上，如果再经过△t=2.5s光束又射到小车上，则小车的速度为多少？（结果保留二位数字）
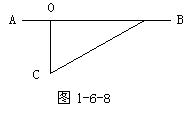20．（14分）如图1-6-8所示，AB、CO为互相垂直的丁字行公路，CB为一斜直小路，CB与CO成600角，CO间距300米，一逃犯骑着摩托车以54Km/h的速度正沿AB公路逃串。当逃犯途径路口O处时，守侯在C处的公安干警立即以1.2m/S2的加速度启动警车，警车所能达到的最大速度为120Km/h。公安干警沿COB路径追捕逃犯，则经过多长时间在何处能将逃犯截获？公安干警抄CB近路到达B处时，逃犯又以原速率掉头向相反方向逃串，公安干警则继续沿BA方向追捕，则经过多长时间在何处能将逃犯截获？（不考虑摩托车和警车转向的时间）
第一章 直线运动参考答案：
第一节 质点运动的基本概念
反馈练习：1．12km/h 2． 0.29s
巩固练习
1．BC 2．BC 3．C 4．D 5．BCD 6．B
7．36、0 8．100 9．S/L 10．425 11．1/H、1×1010
12．225m 、 675m 13．5.83m/s
14．30km、0.5h 15．60m
第二节 匀变速直线运动的规律（Ⅰ）
反馈练习：1．4m/s2、14m/s 2．300m
巩固练习
1．D 2．ABC 3．AD 4．A 5．C 6．C
7．20、0.5、40、400 8．2、5 9．54m、12m/s
10．1.414m/s、7m 11．160s 12．0.7s、5.56m/s2
13．大于31.875m小于等于55m、小于等于31.875m 14．(v12-v22)/2s
15．
第三节 匀变速直线运动的规律（Ⅱ）
反馈练习：1．2m/s2、9.5m 2．大于等于12m/s
巩固练习
1．ABD 2．C 3．D 4．B 5．C 6．A
7．(
)∶(
)∶1 8．（S1+S2）/2t 9．40、200 10. 17、17
11．2s/（t1+t2）、t2∶t1、t1∶t2 12．略
13．1.125m、1m/s2、2.5m/s 14．
m/s、3m/s；4m、4s
15．12.5m；5s、20m/s
第四节 自由落体运动
反馈练习：1．42.05m 2．45m、30m/s
巩固练习
1．AC 2．B 3．ACD 4．AB 5．BCD 6．D 7．D 8．AC
9．40、80 10．40、1∶3∶5
11．15m 12．9m 13．0.5s、15m 14．0.8m 15．291m
第五节 实验：研究匀变速直线运动
反馈练习：1．0.02、0.6、2 2．1.9、2 3．0.55
第六节 第六节 总结、综合与拓展
反馈练习：1．
m/s2 2．2s0
第一章 直线运动总结性测试答案
1．B 2．D 3．B 4．BCD 5．D 6．B 7．AC 8．BC 9．C 10．C
11．（v12-v22）2/2s0 12． 9 13．1/3
14．0.5m/s2、0.33m/s2 15．21m/s、1.53m/s 16．2.25
17．-0.16m/s2、7.2m/s 18．8.5s
19．1.7m/s、2.9m/s
20．41.6s、624m；34.1s、444.6m