期末复习系列讲义—运动的描述

加速度：

（1）描述物体速度变化快慢的物理量，a=△v/△t （又叫速度的变化率），是矢量。a的方向只与△v的方向相同。

　　（2）加速度与速度没有直接关系：加速度很大，速度可以很小、可以很大、也可以为零（某瞬时）；加速度很小，速度可以很小、可以很大、也可以为零（某瞬时）；

　　（3）加速度与速度的变化量没有直接关系：加速度很大，速度变化量可以很小、也可以很大；加速度很小，速度变化量可以很大、也可以很小。加速度是“变化率”——表示变化的快慢，不表示变化的大小。

　　（4）物体是否作加速运动，决定于加速度和速度的方向关系，而与加速度的大小无关。加速度的增大或减小只表示速度变化快慢程度增大或减小，不表示速度增大或减小。

　　当加速度方向与速度方向相同时，物体作加速运动，速度增大；若加速度增大，速度增大得越来越快；若加速度减小，速度增大得越来越慢（仍然增大）。

　　当加速度方向与速度方向相反时，物体作减速运动，速度减小；若加速度增大，速度减小得越来越快；若加速度减小，速度减小得越来越慢（仍然减小）。

1．分析下列运动，研究对象能否当作质点?

　  (1)做花样溜冰的运动员　　 　　　　 (3)转动着的砂轮

　  (2)运行中的人造地球卫星　　　　　  (4)从斜面上滑下的木块　　　

2．关于速度和加速度的关系，下列论述正确的是（　　 ）

A. 加速度大，则速度也大　　　　　　　　  B. 速度的变化量越大，则加速度也越大　　　　

C. 物体的速度变化越快，则加速度就越大　　  D. 速度的变化率越大，则加速度越大

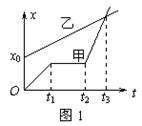3．甲乙两物体在同一直线上运动的。x-t图象如图1所示，以甲的出发点为原点，出发时刻为计时起点则从图象可以看出（　　  ）

A．甲乙同时出发　　　　　　　　　 B．乙比甲先出发

C．甲开始运动时，乙在甲前面x₀处　D．甲在中途停了一会儿，但最后还是追上了乙

４.关于位移和路程，下列说法中正确的是（　　）

A．物体沿直线向某一方向运动，通过的路程就是位移

B．物体沿直线向某一方向运动，通过的路程等于位移的大小

C．物体通过路程不为零，其位移可能为零

D．物体通过的路程不等时，位移可能相同

５．在下述关于位移的各种说法中, 正确的是（　　 ）

　　A．位移和路程是两个量值相同、而性质不同的物理量

　　B．位移和路程都是反映运动过程、位置变化的物理量

C．物体从一点运动到另一点, 不管物体的运动轨迹如何, 位移的大小一定等于两点间的距离

　　D．位移是矢量, 物体运动的方向就是位移的方向

６．关于速度和加速度的关系，下列说法中正确的是（　　）

A．速度变化越大，加速度就越大　C．加速度大小不变，速度方向也保持不变

B．速度变化越快，加速度越大　　Ｄ．加速度大小不断变小，速度大小也不断变小

７．下列说法中正确的是（　　）

　A．平均速度就是速度的平均值　　　C．火车以速度v经过某一段路，v是指瞬时速度

　B．瞬时速率是指瞬时速度的大小　　D．子弹以速度v从枪口射，v是平均速度

８．太阳从东边升起，西边落下，是地球上的自然现象，但在某些条件下，在纬度较高地区上空　飞行的飞机上．可以看到太阳从西边升起的奇妙现象，这些条件是(　　)

  A．时间必须是清晨，飞机正在从东向西飞行，飞机的速率必须较大

  B．时间必须是清晨，飞机正在从西向东飞行，飞机的速率必须较大

  c．时间必须是傍晚，飞机正在从东向西飞行，飞机的速率必须较大

  D．时间必须是傍晚，飞机正在从西向东飞行，飞的速率必须较大

　　　　　　　 期末复习系列讲义－匀变速直线运动　　　

一、匀变速直线运动公式

1．常用公式有以下四个

　　　 　　　　　　　 　　　　　　　　　　　　

2．匀变速直线运动中几个常用的结论

①Δs=aT 2，即任意相邻相等时间内的位移之差相等。可以推广到s_m-s_n=(m-n)aT ²

② ，某段时间的中间时刻的即时速度等于该段时间内的平均速度。

 ，某段位移的中间位置的即时速度公式（不等于该段位移内的平均速度）。

可以证明，无论匀加速还是匀减速，都有 。

3．初速度为零（或末速度为零）的匀变速直线运动

做匀变速直线运动的物体，如果初速度为零，或者末速度为零，那么公式都可简化为：　

　 ，　 ，　 ，　

4．初速为零的匀变速直线运动

①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……

②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……

　　③前1米、前2米、前3米……所用的时间之比为1∶∶∶……

　　④第1米、第2米、第3米……所用的时间之比为1∶∶（）∶……

对末速为零的匀变速直线运动，可以相应的运用这些规律。

二、匀变速直线运动的特例

1．自由落体运动

（1）特点：加速度为g，初速度为零的匀加速直线运动。

（2）规律：v_t=gt　　 h =gt­²  v_t² =2gh

三.：解题方法：

（1）公式解析法：假设未知数，建立方程组。本章公式多，且相互联系，一题常有多种解法。要熟记每个公式的特点及相关物理量。

（2）图象法：如用v—t图可以求出某段时间的位移大小、可以比较与v，以及追及问题。用x—t图可求出任意时间内的平均速度。

（3）比例法：用已知的结论，用比例的性质求解。

（4）极值法：用二次函数配方求极值，追赶问题用得多。

（5）逆向思维法：如匀减速直线运动可视为反方向的匀加速直线运动来求解。

追赶问题：

1．两个关系：即时间关系和位移关系

2．一个条件：即两者速度相等，它往往是物体间能否追上、追不上或（两者）距离最大、最小的临界条件，也是分析判断的切入点。

常见的情况有：

（1）物体A追上物体B：开始时，两个物体相距s₀，则A追上B时，必有s_A-s_B=s₀，且v_A≥v_B。

（2）物体A追赶物体B：开始时，两个物体相距s₀，要使两物体恰好不相撞，必有s_A-s_B=s₀，且v_A≤v_B。

1．物体M从A运动到B，前半程平均速度为v₁，后半程平均速度为v₂，那么全程的平均速度是：

A．（v₁+v₂）/2　　  B．　　 C．　　 D．

２．物体从斜面顶端由静止开始滑下，经ts到达中点，则物体从斜面顶端到底端共用时间为

A．s　　　　　　B.s　　　　　　　C.2t s 　　　　 D.t s

３根据打点计时器打出的纸带，我们可以不利用公式计算就能直接得到的物理量是（　　）

A、时间间隔　　　 B、位移　　  C、加速度　　　　 D、平均速度

４．在与x轴平行的匀强电场中，一带电量q=1.0×10-8C、质量m=2.5×10-3kg的物体在光滑水平面上沿着x轴作直线运动，其位移与时间的关系是x＝0.16t－0.02t2，式中x以m为单位，t以s为单位。从开始运动到5s末物体所经过的路程为　　　　m, 位移为　　　　m. 　

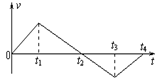5、如图所示是物体运动的v-t图象，从t=0开始，对原点的位移最大的时刻是（　　  ）

A、t₁　　　B、t₂ 　C、t₃ D、t₄

6、一辆汽车从车站以初速度为零匀加速直线开去，开出一段时间之后，司机发现一乘客未上车，便紧急刹车做匀减速运动.从启动到停止一共经历t=10 s，前进了15m，在此过程中，汽车的最大速度为（　　）

A、1.5 m/s　　　B、3 m/s  C、4 m/s　　　　　D、无法确定

7、汽车正在以 20m/s的速度在平直的公路上前进，司机突然发现正前方46m处有一物体挡在路上，便关闭油门做匀减速直线运动，司机的反应时间为0.3s；若汽车不碰上物体，汽车的加速度大小至少为（　　）

A、2.5m/s2　　　B、5m/s2　 C、7.5m/s2　　　　 D、10m/s2

８．甲、乙两位同学做测定反应时间的小实验，甲同学的两个手指捏住直尺的上端，乙同学用一只手在直尺下端做准备。当看到甲同学放手后，乙同学立即捏住直尺，发现直尺下降了0.2m，则乙同学的反应时间是　　　 （取g=10m/s）　

９．将一条铁链的一端悬挂于天花板上，无初速释放此铁链使它作自由落体运动，已知铁链通过悬点下方3.2m处的一点P历时0.5s，铁链的长度为？（g取10m/s²）

　１０．驾驶员手册规定：具有良好刹车性能的汽车以80 km/h的速率行驶时，从操纵刹车到最终停止运动距离为56m，在以48km/h的速率行驶时，从操纵刹车到最终停止运动距离为24m。假设对于两种速率，驾驶员所允许的反应时间（在反应时间内驾驶员来不及使用刹车，车速不变）与刹车的负加速度都相同，则允许驾驶员的反应时间为多少？

　１１．经检测汽车A的制动性能：以标准速度20m/s在平直公路上行使时，制动后40s停下来。现A在平直公路上以20m/s的速度行使发现前方180m处有一货车B以6m/s的速度同向匀速行使，司机立即制动，能否发生撞车事故？