弹簧与传送带专题

内容提要：

一、弹簧问题：

1、弹簧的瞬时问题

弹簧的两端都有其他物体或力的约束时，使其发生形变时，弹力不能由某一值突变为零或由零突变为某一值。

2、弹簧的平衡问题

这类题常以单一的问题出现，涉及到的知识是胡克定律，一般用f=kx或△f=k•△x来求解。

3、弹簧的非平衡问题

这类题主要指弹簧在相对位置发生变化时，所引起的力、加速度、速度、功能和合外力等其它物理量发生变化的情况。

4、 弹力做功与动量、能量的综合问题

在弹力做功的过程中弹力是个变力，并与动量、能量联系，一般以综合题出现。它有机地将动量守恒、机械能守恒、功能关系和能量转化结合在一起，以考察学生的综合应用能力。分析解决这类问题时，要细致分析弹簧的动态过程，利用动能定理和功能关系等知识解题。

二、传送带问题：

传送带类分水平、倾斜两种：按转向分顺时针、逆时针转两种。

（1）受力和运动分析：

受力分析中的摩擦力突变（大小、方向）——发生在V物与V传相同的时刻；运动分析中的速度变化——相对运动方向和对地速度变化。分析关键是：一是 V_物、V_带的大小与方向；二是mgsinθ与f的大小与方向。

(2)传送带问题中的功能分析

　　①功能关系：WF=△E_K+△E_P+Q

　　②对W_F、Q的正确理解

　　（a）传送带做的功：W_F=F·S_带　 功率P=F×V_带（F由传送带受力平衡求得）

　　（b）产生的内能：Q=f·S_相对

　　（c）如物体无初速，放在水平传送带上，则在整个加速过程中物体获得的动能E_K，因为摩擦而产生的热量Q有如下关系：E_K=Q=

典型例题：

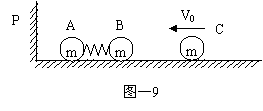
例1：在原子物理中，研究核子与核子关联的最有效途经是“双电荷交换反应”。这类反应的前半部分过程和下面力学模型类似。两个小球A和B用轻质弹簧相连，在光滑的水平直轨道上处于静止状态。在它们左边有一垂直轨道的固定档板P，右边有一小球C沿轨道以速度v₀射向B球，如图7所示，C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变。然后，A球与档板P发生碰撞，碰后A、D静止不动，A与P接触而不粘连。过一段时间，突然解除销定（锁定及解除锁定均无机械能损失），已知A、B、C三球的质量均为m。

（1）求弹簧长度刚被锁定后A球的速度。

（2）求在A球离开档板P之后的运动过程中，弹簧的最大弹性势能。

解：整个过程可分为四个阶段来处理．
　　（1）设Ｃ球与Ｂ球粘结成Ｄ时，D的速度为ｖ_１，由动量守恒定律，得
　　　　　　 ｍｖ_０＝2ｍｖ_１，　①
　　当弹簧压至最短时，Ｄ与Ａ的速度相等，设此速度为ｖ_２，由动量守恒定律，得
　　　　　　2ｍｖ_１＝3ｍｖ_２，　②
联立①、②式得
　　　　　 ｖ_１＝（1／3）ｖ_０．　③
　　此问也可直接用动量守恒一次求出（从接触到相对静止）ｍｖ_０＝3ｍｖ_２，ｖ_２＝（1／3）ｖ_０．
　　（2）设弹簧长度被锁定后，贮存在弹簧中的势能为Ｅｐ，由能量守恒定律，得
　　　 （2ｍ）ｖ_１^２＝（3ｍ）ｖ_２^２＋Ｅ_ｐ，　④
　　撞击Ｐ后，Ａ与Ｄ的动能都为零，解除锁定后，当弹簧刚恢复到自然长度时，弹性势能全部转变成Ｄ的动能，设Ｄ的速度为ｖ_３，有
　　Ｅ_ｐ＝（2ｍ）ｖ_３^２，　⑤
　　以后弹簧伸长，Ａ球离开挡板Ｐ，并获得速度．设此时的速度为ｖ_４，由动量守恒定律，得
　　2ｍｖ_３＝3ｍｖ_４，　⑥
　　当弹簧伸到最长时，其弹性势能最大，设此势能为Ｅ_ｐ′，由能量守恒定律，得
　　（2ｍ）ｖ_３^２＝（3ｍ）ｖ_４^２＋Ｅ_ｐ′，　⑦
联立③～⑦式得
　　Ｅ_ｐ′＝ｍｖ_０^２．　⑧
　　评析　今年的高考压轴题不愧为一道好的物理试题．命题人暗设机关，巧布干扰，只有当考生全面读懂、领会题意，并在头脑中建立起非常清晰的物理图景和过程，充分运用两个守恒定律，化难为易，变繁为简，才能明察秋毫，予以识破．

例2：（2005年全国理综II卷）如图，质量为的物体A经一轻质弹簧与下方地面上的质量为的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩。开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向。现在挂钩上升一质量为的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升。若将C换成另一个质量为的物体D，仍从上述初始位置由静止状态释放，则这次B刚离地时D的速度的大小是多少？已知重力加速度为g。

　解：开始时，A、B静止，设弹簧压缩量为x₁，有　 kx₁=m₁g　　 ①

　　挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x₂，有

　　kx₂=m₂g　　　　  ②

　　B不再上升，表示此时A和C的速度为零，C已降到其最低点。由机械能守恒，与初始状态相比，弹簧性势能的增加量为

　　△E=m₃g(x₁+x₂)－m₁g(x₁+x₂)　 ③

　　C换成D后，当B刚离地时弹簧势能的增量与前一次相同，由能量关系得

　　　 ④

　　由③④式得　　　 ⑤

　　由①②⑤式得

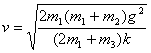　⑥

综上举例，从中看出弹簧试题的确是培养、训练学生物理思维和反映、开发学生的学习潜能的优秀试题。弹簧与相连物体构成的系统所表现出来的运动状态的变化，是学生充分运用物理概念和规律（牛顿第二定律、动能定理、机械能守恒定律、动量定理、动量守恒定律）巧妙解决物理问题、施展自身才华的广阔空间，当然也是区分学生能力强弱、拉大差距、选拔人才的一种常规题型。因此，弹簧试题也就成为高考物理的一种重要题型。而且，弹簧试题也就成为高考物理题中一类独具特色的考题

例3、如图所示，倾角为30°的皮带运输机的皮带始终绷紧，且以恒定速度v＝2.5m/s运动，两轮相距L_AB＝5m，将质量m＝1kg的物体无初速地轻轻放在A处，若物体与皮带间的动摩擦因数μ＝ ．(取g＝10m/s²）

①　　 物体从A运动到Ｂ,皮带对物体所做的功是多少?②物体从A运动到B共需多少时间?

③ 在这段时间内电动机对运输机所做的功是多少?

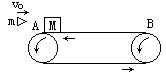例4、如图所示，水平传送带AB长l＝8.3m，质量为M＝1kg的木块随传送带一起以v1＝2m/s的速度向左匀速运动（传送带的传送速度恒定），木块与传送带间的动摩擦因数μ＝0.5。当木块运动至最左端A点时，一颗质量为m＝20g的子弹以v0＝300m/s水平向右的速度正对射入木块并穿出，穿出速度u＝50m/s，以后每隔1s就有一颗子弹射向木块，设子弹射穿木块的时间极短，且每次射入点各不相同，g取10m/s²，求：

（1）在被第二颗子弹击中前木块向右运动离A点的距离？

（2）木块在传送带上最多能被多少颗子弹击中？

（3）从第一颗子弹射中木块到木块最终离开传送带的过程中，子弹、木块和传送带这一系统所产生的热能是多少？（g取10m/s²）

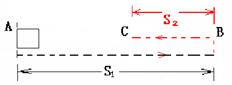
T=1s内木块的合位移为s=0.5m,方向向右

提高练习：

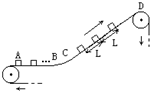
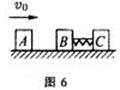1、对如图所示的皮带传动装置，下列说法中正确的是　BD

(A)A 轮带动B 轮沿逆时针方向旋转．

(B)B 轮带动A 轮沿逆时针方向旋转．

(C)C 轮带动D 轮沿顺时针方向旋转．

(D)D 轮带动C 轮沿顺时针方向旋转．

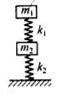2、如图2所示，两个木块质量分别为m₁和m₂，两轻质弹簧的劲度系数分别为k₁和k₂，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态，现缓慢向上提上面的木块，直到它刚离开上面的弹簧，在这过程中下面木块移动的距离为：

分析和解：此题用整体法求最简单。由题意可将图2改为图3所示，这样便于分析求解，当m₁、m₂视为一系统（整体）时，整个系统处于平衡状态，即∑F=0

评析：尽管此题初看起来较复杂，但只需选用整体法来分析求解，问题就会迎刃而解。

3、如图4所示，质量为m的物体A放置在质量为M的物体B上，B与弹簧相连，它们一起在光滑水平面上作简谐振动，振动过程中A、B之间无相对运动。设弹簧的劲度系数为k，当物体离开平衡的位移为x时，A、B间磨擦力的大小等于　 （　 ）

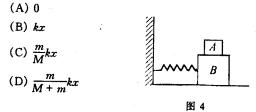
分析和解：此题属于简谐振动。当物体位移为x时，根据题意将M、m视为整体，由胡克定律和牛顿第二定律，得：

再选A为研究对象，使A随B振动的回复力只能是B振动的回复力只能是B对A的静磨擦力，由f=ma　　　　　 ③

联立①②③得，故选（D）

4、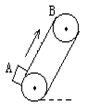如图所示，倾角为30°的皮带运输机的皮带始终绷紧，且以恒定速度v＝2.5m/s运动，两轮相距L_AB＝5m，将质量m＝1kg的物体无初速地轻轻放在A处，若物体与皮带间的动摩擦因数μ＝ (取g＝10m/s²）

①　　 物体从A运动到Ｂ,皮带对物体所做的功是多少?

②　　 物体从A运动到B共需多少时间?

③ 在这段时间内电动机对运输机所做的功是多少?

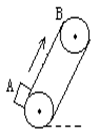
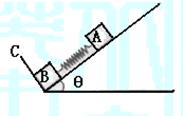5、（2005年全国理综III卷）如图所示，在倾角为的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为m_A、m_B，弹簧的劲度系数为k,C为一固定挡板。系统处一静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d，重力加速度为g。

解：令x₁表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知

　 ①

令x₂表示B刚要离开C时弹簧的伸长量， a表示此时A的加速度，由胡克定律和牛顿定律可知：

　　kx₂=m_Bgsinθ　 ②

　　F－m_A­gsinθ－kx₂=m_Aa　 ③

　　由②③式可得　④

　　由题意 d=x₁+x₂　　⑤

　　由①②⑤式可得　 ⑥

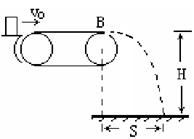7、如图所示，水平传送带水平段长L＝6m，两皮带轮直径D均为0.2m，距地面高H＝5m，与传送带等高的光滑水平台上有一小物块以v0＝5m/s的初速度滑上传送带，物块与传送带间动摩擦因数μ＝0.2，g取10m/s2.求(1)若传送带静止,物块滑到B端后做平抛运动的水平距离S(2)若皮带轮顺时针以角速度ω＝60rad/s转动，物块滑到B端后做平抛运动的水平距离S’。

　　8、如右图为一皮带传动装置，传送带与水平面夹角为θ，A、B轮半径均为R，轴心间距为L，B轮由电动机带动，其传速为n。在货物随皮带运动过程中,有一小球由静止开始沿光滑轨道滚下，到达传送带时,货物恰好运到传送带中央，当货物运动到距B轮L/4的C点时，小球恰好与货物相遇而未发生碰撞.若皮带不打滑,且货物总与皮带保持相对静止，试求：（1）货物由传送带中央运动到C点所用时间（2）轨道顶端与底端的高度差h。

 

　

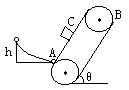
 9、一传送带装置示意如图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形（圆弧由光滑模板形成，未画出），经过CD区域时是倾斜的，AB和CD都与BC相切.现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零，经传送带运送到D处，D和A的高度差为h。稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L。每个箱子在Ａ处投放后,在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段时的微小滑动）.已知在一段相当长的时间T内，共运送小货箱的数目为Ｎ.这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.求电动机的平均输出功率。