曲线运动、平抛运动

知识要点

（一）曲线运动

1. 曲线运动定义：轨迹是曲线的运动。

2. 曲线运动的速度方向和性质：做曲线运动的物体其速度方向时刻在改变，速度是矢量，故曲线运动一定是变速运动，做曲线运动的物体在某一点的瞬时速度方向在曲线的这一点的切线上。

3. 物体做直线运动条件：物体所受合外力为零或所受合外力方向和物体运动方向在同一直线上。

4. 物体作曲线运动条件：加速度方向与速度方向不在一条直线上，且加速度方向指向曲线的凹侧。

5. 当物体做曲线运动时它所受的合外力与它的速度方向不在一条直线上，那么合外力可分解为垂直速度方向和沿速度方向的两个分力，垂直速度方向的分力起到改变速度方向的作用，沿速度方向的分力将改变速度的大小，若该分力与速度方向相同，物体速度将增大；若该分力与速度方向相反，速度将减小；若该分力为零，则物体将做匀速圆周运动。

（二）运动的合成和分解

1. 有关运动的合成和分解的几个概念：（结合课本实验红蜡块的运动引入）

如果某物体同时参与几个运动，那么这物体实际运动就叫做那几个运动的合运动，那几个运动叫做这个实际运动的分运动。已知分运动情况求合运动情况叫运动的合成，已知合运动情况求分运动情况叫运动的分解。

合运动的位移叫做合位移；分运动的位移叫分位移。合运动在一段时间内的平均速度叫合速度；分运动在该同一段时间内的平均速度叫分速度。

2. 运动的合成及分解规则：平行四边形定则。

（1）合运动一定是物体的实际运动。

（2）分运动之间是相互不相干的。　　　　　　　　　　　　　　　  　

（3）合运动和各分运动具有等时性。　

（4）合运动和分运动的位移、速度、加速度都遵守平行四边形定则。

（5）特例：

① 初速为的匀加速直线运动，可看成是同方向的一个匀速运动和另一个初速为零的匀加速直线运动的合运动；

② 竖直上抛运动可看成是一个竖直向上的匀速直线运动和另一个自由落体运动的合运动；

③ 两个匀速直线运动合成后一定是匀速直线运动；

④ 不在同一直线上的一个匀速直线运动和一个变速直线运动合成后运动轨迹是曲线（合运动的加速度方向和合运动速度方向不在同一直线上）。

3. 两个直线运动的合成：

① 两个匀速直线运动合成的运动是匀速直线运动。

② 两个匀变速直线运动的合运动，当它们的初速度的合速度方向和加速度的合加速度的方向在一条直线上时，合运动是匀变速直线运动，否则将是匀变速曲线运动。

③ 一个匀速直线运动和一个匀变速直线运动的合运动，当它们的初速度方向和与加速度方向在一条直线上时，合运动是匀变速直线运动，反之，当它们的初速度方向和与加速度方向不在一条直线上时，合运动将是匀变速曲线运动。

④ 一个匀速直线运动和一个方向与它垂直的初速度为零的匀加速运动的合运动，一定是匀变速曲线运动。

4. 渡河问题：渡河问题所涉及的就是渡河的最短时间问题和渡河的最短位移问题。

① 最短时间问题：无论、，还是，只要沿垂直于河岸方向渡河，则所用时间最短，此时（其中d为河宽）

② 渡河的最短位移问题：

i. 当时，与河岸垂直，充当斜边，。

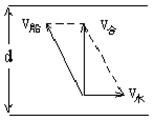
图1

ii. 当时，无最短位移。

iii. 当时，以的箭头为圆心，以的大小为半径画弧，以的箭尾为起点做圆弧的切线，延长该切线到对岸，即为最短位移，由三角形相似

∴。

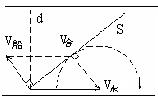
图2

（三）平抛运动

  1. 平抛运动的定义：水平抛出物体只在重力作用下的运动。

  2. 平抛运动性质：是加速度恒为重力加速度g的匀变速曲线运动，轨迹是抛物线。

3. 平抛运动的处理方法：（结合课本的演示实验进行讲解）

　分解为

　　

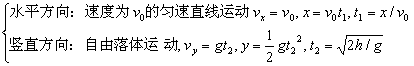
结果得

　

注意：运动学公式只适用于直线运动，因此曲线运动要分解成两个直线的分运动后才能应用运动学公式求解。

4. 平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。这两个分运动同时存在，按各自的规律独立进行，水平初速度的大小不会影响竖直方向的分运动。一般情况下，竖直方向的分运动决定着平抛物体的运动的时间。

5. 平抛运动的轨迹。

设物体做平抛运动到某点P（，），如图3所示，则轨迹方程为，消去参数，得（抛物线）。

平抛物体经一段时间，其速度方向和位移方向是不相同的，如图3所示。

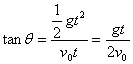，，即。

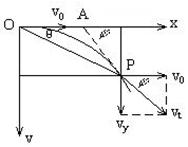
图3

6. 如图3所示，曲线上任一点P（，）的速度方向反向延长线交于轴上的A点，由图3可知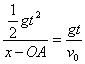，所以OA=。

7. 平抛物体在相同时间内，速度变化量相同，，且方向为竖直向下，如图4所示。

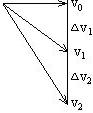
图4

【典型例题】

[例1] 小船在200m宽的河中横渡，水流速度是2m／s，船在静水中的速度是4m／s，求：

① 当小船的船头始终正对对岸时，它将在何时、何处到达对岸？ ② 要使小船到达正对岸，小船应如何行驶？耗时多少？

解析：小船参与了两个分运动，随水漂流和船在静水中的运动。因为运动具有独立性，分运动之间互不干扰，即渡河时间由船的指向和其静水中的速度决定，沿河运动的距离由水的流速决定。所以：渡河时间等于垂直河岸分运动的时间s

沿河方向的位移m=100m，即小船在正对河岸下游100m处靠岸。

要使小船垂直过河，即合速度应垂直河岸如图5所示，则　 所以：　，即的方向与上游河岸成

s

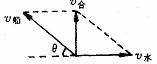
图5

[例2] 以16m／s的速度水平抛出一石子，石子落地时的速度方向与抛出时的速度方向成角，不计空气阻力，那么石子抛出点与落地点的高度差是多少？石子的落地速度是多少？

解析：石子落地时的速度是合速度，可分解为水平和竖直两个方向的分速度，如图6所示：

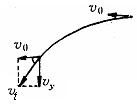
图6

由三角形关系可知，m/s，因竖直方向是自由落体运动。故，得s，下落高度m，落地速度m/s．

[例3] 如图7所示，水平面上有一物体，小车通过定滑轮用绳子拉它，在图7所示位置时，若小车的速度为5m/s，则物体的瞬时速度为___________m/s

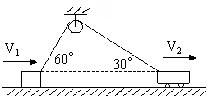
图7

解析：由小车的速度为5m/s，小车拉绳的速度　 则物体受到绳的拉力。

拉绳的速度，则物体的瞬时速度为。

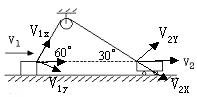
图8

【模拟试题】

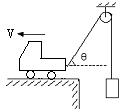
1. 如图所示，汽车以速度v匀速行使，当汽车到达P点时，绳子与水平方向的夹角θ，此时物体M的速度大小为__________（用v、θ表示）

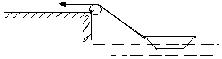
2. 如图所示，在河岸上用细绳拉船，为了使船匀速靠岸，拉绳的速度必须是（　　）

A. 加速拉　　　　　　  B. 减速拉

C. 匀速拉　　　　　　  D. 先加速后减速

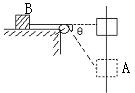
3. 如图所示，以速度v沿竖直杆匀速下滑的物体A，用细绳通过定滑轮拉物体B在水平面上运动，当绳与水平面夹角为θ时，物体B运动的速率为_______。

4. 河水流速= 5m/s，船在静水中的船速= 4m/s，河宽d=100m，则船渡河的最小航程多大？

5. 有一小船正在渡河，离对岸50m，已知在下游120m处有一危险区，假设河水流速为5m/s，为了使小船不通过危险区到达对岸，那么小船从现在起相对静水的最小速度应是（　　 ）

A. 2.08 m/s　　　　B. 1.92 m/s　　　  C. 1.58 m/s　　　 D. 1.42 m/s

6. 某人乘船横渡一条河，在静水中的速度及水速一定，此船过河的最短时间为，若此船用最短位移过河，则需时间为，若船速大于水速，则船速与水速之比为多少？

7. 一只船在静水中的速度为3m/s，它要横渡一条30m宽的河，水流速度为4m/s，下列说法正确的是（　　 ）

A. 这只船不可能垂直河岸抵达正对岸

B. 这只船对地的速度一定是5m/s

C. 过河时间可能是6s

D. 过河时间可能是12s

8. 如图所示，MN是流速稳定的河流，船在静水中的速度为v，自一岸的P点渡河，船速v方向垂直河岸，10min船到A点，已知OA=120m（OP与河岸垂直）如v的方向与OP线成α角，则经12.5min船到O点，则（　　 ）

A. α= arc cos　　　　 B. 河宽为200米

C. 水速为2m/s　　　　　　　 D. 船速v=m/s

 

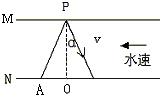
9. 如图所示，MN是水流速度稳定的河流，小船在静水中的速度为，船自A点渡河，第一次沿AB方向，第二次沿AC方向，两次渡河所用的时间分别为和，若AB和AC与河岸的夹角相等，则（　　 ）

A. 两方向若为船航行的分速度方向，则=

B. 两方向若为船航行的分速度方向，则 >

C. 两方向若为船航行的合速度方向，则=

D. 两方向若为船航行的合速度方向，则>

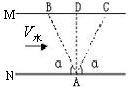
10. 甲乙两船在同一条河流中同时开始渡河，河宽为H ，河水流速为u，滑船速度为v，出发时两船相距H，甲乙船头均与岸边成60°角，且乙船恰好能垂直到达对岸的A点，如图，则（　　 ）

A. 甲乙两船到达对岸时间不同　　　　　　　 B. v =2u

C. 两船可能在未到对岸前相遇　　　　　  D. 甲船也在A点靠岸

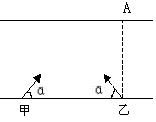
11. 在不同高度以相同的水平速度抛出的物体，若落地点的水平位移之比为∶1，则抛出点距地面的高度之比（　　）

A. 1:1　 　　B. 2:1　　　C. 3:1　　　 D. 4:1

12. 某质点以9.8m/s的初速度做平抛运动，经过一段时间后的末速度为初速度的倍，则这段时间是（g取9.8m/s²）（　　）

A. S　　 　B. S　　 C. S　 　D. S　　

13. A、B、C三小球从同一竖直线上的不同高度处水平抛出（不计空气阻力），下落在同一地点。已知三小球的初始位置高度之比为∶∶=3∶2∶1则三小球抛出时初速度大小之比为∶∶=________。

14. 炮台高出海面45m，炮弹的水平出口速度为600m/s。如果要使炮弹击中一艘正以36km/ h的速度沿直线远离炮台逃跑的敌舰，那么应在敌舰离炮台________m处开炮。

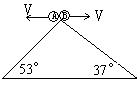
15. 如图所示，相对的两个页面，倾角分别为37º和53º，在顶点把两小球以相同大小的初速度分别向左、右水平抛出，小球都落在斜面上，若不计空气阻力，则A、B两球运动时间之比为（　　 ）

A. 1:1　　　 B. 4:3　　　 C. 16:9　　　 D. 9:16

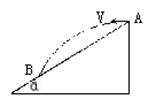
16. 如图所示，在倾角为α的斜面上A点，以初速度v₀水平抛出一小球，小球落在斜面上的B点，不计空气阻力，求小球落到B点的速度多大？

17. 一物体从某高度以初速度水平抛出，落地时的速度为，则它的运动时间为（　　 ）

A. 　　　　B. 　　 C、　　  D.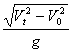

【试题答案】

1. 　　　 2. B　　　 3. 　　　 4. 125m　　　 5. B　

6. 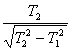　　7. AD　　　8. ABD　　　　　9. AD　　　　10. BD

11. C　 　　　　 12. B　　　 13. :: 　　　14. 1770m　　　　

15. C 　　　　　 16. 　　　　　　　 17. D