机械能专题
(一)对功的认识
1. 做功与否的判断问题
物体受到力的作用,如果物体在力的方向上发生位移,我们就说力对物体做了功。可见做功与否的判断,依据的是功的两个要素:力与力的方向上的位移。
2. 做功多少的计算问题
做功多少是根据功的公式来计算的,功的公式为:![]() ,其中各个物理量的含义如下:F是做功的力;s是力所作用的那个物体的位移;而
,其中各个物理量的含义如下:F是做功的力;s是力所作用的那个物体的位移;而![]() 则是力F与位移s之间的夹角。
则是力F与位移s之间的夹角。
3. 做功快慢的描述问题
做功的快慢程度用功率来描述,功率的定义式是:![]()
功率的导出式是:![]()
前者用于计算某段时间内的平均功率,后者则用于计算某个时刻瞬时功率。
4. 对功的物理含义的理解
关于功我们不仅要从定义式![]() 进行理解和计算,还应理解它的物理含义。功是能量转化的量度,即:做功的过程是能量的一个转化过程,这个过程做了多少功,就是多少能量发生了转化。对物体做正功,物体的能量增加。对物体做了多少正功,物体的能量就增加了多少;对物体做负功,也称物体克服阻力做功,物体的能量减少,做了多少负功,物体的能量就减少了多少。因此功的正、负表示能的转化情况,表示物体是输入了能量还是输出了能量。
进行理解和计算,还应理解它的物理含义。功是能量转化的量度,即:做功的过程是能量的一个转化过程,这个过程做了多少功,就是多少能量发生了转化。对物体做正功,物体的能量增加。对物体做了多少正功,物体的能量就增加了多少;对物体做负功,也称物体克服阻力做功,物体的能量减少,做了多少负功,物体的能量就减少了多少。因此功的正、负表示能的转化情况,表示物体是输入了能量还是输出了能量。
[例1] 如图1所示,质量为m的物体静止于倾角为![]() ,质量为M的斜面体上,现对该斜面体施一水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动,位移为s,求在此过程中物体所受重力、支持力、摩擦力各对物体做了多少功?
,质量为M的斜面体上,现对该斜面体施一水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动,位移为s,求在此过程中物体所受重力、支持力、摩擦力各对物体做了多少功?
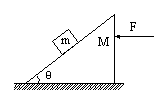
图1
析与解:物体的受力情况如图2所示,由于物体处于匀速运动状态,可由共点力的平衡条件得,![]() ,
,![]() ,且
,且![]() 与s间的夹角为
与s间的夹角为![]() ,
,![]() 与s间的夹角为
与s间的夹角为![]() ,所以:
,所以:![]()
![]()
![]()

图2
说明:若力和位移不在一条直线,求力对物体做功时,可将力正交分解,使其一个分力与位移在一条直线上,另一个分力与位移垂直,也可以将位移按类似的方法正交分解。
(二)对功率的认识
1. 功率是描述做功快慢的物理量
由![]() 可知,功率的大小只与其“比值”有直接联系,与做功多少和时间长短无直接关联,比较功率的大小就要比较功与完成这些功的所用时间之“比值”。“比值”大,功率就大,做功就快,“比值”小,功率就小,做功就慢。
可知,功率的大小只与其“比值”有直接联系,与做功多少和时间长短无直接关联,比较功率的大小就要比较功与完成这些功的所用时间之“比值”。“比值”大,功率就大,做功就快,“比值”小,功率就小,做功就慢。
物体做功功率是描述物体做功的一个状态;做功的多少是一个过程,所以不能说功率大,做功就多。物体做功多少是做功物体在做功过程中的一个积累,随着做功过程的积累时间越长,这个物体做功就越多,![]() 就是一个积累的意思。即P在时间t上的积累就是物体做功的多少。
就是一个积累的意思。即P在时间t上的积累就是物体做功的多少。
2. 对力的功率的认识
由![]() 、
、![]() 可得:
可得:![]() ,此式中
,此式中![]() 为力F与速度
为力F与速度![]() 之间的夹角。把
之间的夹角。把![]() 当作整体来看是物体在力的方向上的分速度,即:作用在物体上的力与物体在力的方向上分速度的乘积叫做力的功率。
当作整体来看是物体在力的方向上的分速度,即:作用在物体上的力与物体在力的方向上分速度的乘积叫做力的功率。
对一个动力机械,当功率P一定时,由![]() 可知:降低运动速度可以增大牵引力;反过来,若阻力很小,可以加快运动速度。这一点在各种机械设备中有着广泛的应用。
可知:降低运动速度可以增大牵引力;反过来,若阻力很小,可以加快运动速度。这一点在各种机械设备中有着广泛的应用。
任何机械都有一个铭牌,铭牌上所注功率为这部机械的额定功率。它是提供人们对机械进行选择、配置的一个重要参数,它反映了机械的做功能力或机械所能承担的“任务”。机械运行过程中的功率是实际功率。机械的实际功率可以小于其额定功率(俗称机械没吃饱),可以等于其额定功率(称满负荷运行),还可以在短时间内略大于其额定功率(称超负荷运行)。机械不能长时间超负荷运行,那样会损坏机械设备,缩短其使用寿命。
3. 机车的两种启动
(1)机车以恒定功率启动,牵引力随速度的增大而减小,机车做加速度逐渐减小的变加速运动。当加速度减小到零时速度最大,以后机车做匀速运动(牵引力等于阻力)。如图3所示机车以恒定功率启动的P—t图和v—t图。(机车在水平面运动,阻力视为恒定)
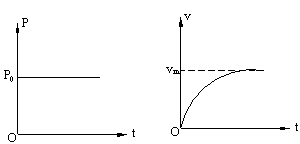
图3
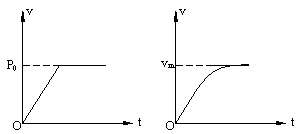
图4
(2)机车匀加速启动,机车先做初速为零的匀加速运动。功率随时间正比例增大,当增大到额定功率时,开始做一段变加速运动,牵引力减小到等于阻力时,机车的速度增大到最大速度。如图4为机车以匀变速启动的P—t和v—t图。
例2:汽车发动机的额定牵引功率为60kW,汽车质量为![]() ,汽车在水平路面上行驶时,阻力是车重的
,汽车在水平路面上行驶时,阻力是车重的![]() 倍,试问(取
倍,试问(取![]() ):
):
(1)汽车保持以额定功率从静止起动后能达到的最大速度是多少?
(2)若汽车从静止开始,保持以![]() 的加速度做匀加速直线运动,这一过程能维持多长时间?
的加速度做匀加速直线运动,这一过程能维持多长时间?
析与解:
(1)汽车一开始就保持额定功率,牵引力随速度的增大而减小,汽车做加速度逐渐减小的变加速运动,当加速度减小到零时速度最大。
此时,![]() ,
,![]()
所以![]()
(2)汽车以恒定加速度起动,先做初速为零的匀加速运动,功率随时间正比例增大,当增大到额定功率时,开始做变加速运动。设保持匀加速运动的时间为t,匀加速运动能达到的最大速度为![]() ,则:
,则:
 ,所以
,所以![]()
(三)对动能的认识
1. 动能是一个状态量,它与物体的运动状态对应。动能也是标量,它只有大小,没有方向,而且物体的动能总是大于等于零,不会出现负值。
动能具有相对性,它与参照物的选取有关。如:在行驶中汽车上的物体,对汽车上的乘客,物体动能为零;但对路边的行人,物体的动能不为零。
2. 外力对物体做功与物体动能的关系:
外力对物体做正功,物体的动能增加,这一外力有助于物体的运动,是动力;外力对物体做负功,物体的动能减小,这一外力是阻碍物体的运动,是阻力,外力对物体做负功往往又称物体克服阻力做功。功是能量转化的量度,外力对物体做了多少功;就有多少动能与其他形式的能发生了转化。所以外力对物体所做的功就等于物体动能的变化量,即![]() 。这就是动能定理。
。这就是动能定理。
3. 应用动能定理的注意点:
(1)明确研究对象、研究过程,找出初、末状态的速度情况。
(2)要对物体进行正确的受力分析(包括重力),明确各力做功的大小及正负情况。
(3)若物体运动过程中包含几个不同物理过程,解题时,可以分段考虑,也可视为一整体过程,列出动能定理求解。
4. 关于动能与动量的比较
(1)动能与动量都是由质量和速度共同决定的物理量;
(2)动能和动量都是用于描述物体机械运动的状态量;
(3)动能是标量,动量是矢量;
(4)动能决定了物体克服一定阻力能运动多远,动量则决定着物体克服一定阻力能运动多长时间;
(5)动能是从能量观点出发描述机械运动的,动量是从机械运动本身出发描述机械运动状态的。
例3:总质量为M的列车,沿水平直线轨道匀速前进,其末节车厢质量为m,中途脱钩,司机发觉时,机车已行驶了L距离,于是立即关闭油门撤去牵引力。设运动的阻力与质量成正比,比例系数为k,机车的牵引力恒定,当列车的两部分都停止时,它们的距离是多少?
析与解:设牵引力为F,脱钩前列车的速度为![]() ,脱钩后两部分的位移分别为
,脱钩后两部分的位移分别为![]() 、
、![]() 。对列车脱钩到静止的全过程,由动能定理:
。对列车脱钩到静止的全过程,由动能定理:![]() ,对末节车厢,脱钩后运动的全过程,由动能定理:
,对末节车厢,脱钩后运动的全过程,由动能定理:![]() ,由脱钩前列车匀速运动得:
,由脱钩前列车匀速运动得:![]() ,解得:
,解得:![]() 。
。
本题也可用补偿法进行分析。若末节车厢脱钩时司机关闭油门,则两部分运动情况完全相同,停止时它们的距离为0,脱钩后牵引力做了![]() 的功,才使两部分拉开距离,这部分功补偿机车多行驶距离中克服阻力所做的功。
的功,才使两部分拉开距离,这部分功补偿机车多行驶距离中克服阻力所做的功。![]() ,所以
,所以![]() 。
。
点评:本题还可以用运动学知识与牛顿第二定律求解,但较繁杂,显然,用补偿法求解则简单快捷,所以平时做题要注意进行解题方法总结。
(四)对重力势能的认识
1. 重力势能是物体和地球这一系统共同所有,单独一个物体谈不上具有势能。即:如果没有地球,物体谈不上有重力势能,平时说物体具有多少重力势能,是一种习惯上的简称。
2. 重力势能是标量,它没有方向。但是重力势能有正、负。此处正、负不是表示方向,而仅表示比参考点的能量状态高还是低。势能大于零表示比参考点的能量状态高,势能小于零表示比参考点的能量状态低。参考点的选择不同虽对势能值表述不同,但对物理过程没有影响,即势能是相对的,势能的变化是绝对的,势能的变化与参考点的选择无关。
3. 重力做功与重力势能
重力做正功,物体高度下降,重力势能降低;重力做负功,物体高度上升,重力势能升高。可以证明,重力做功与路径无关,由物体所受的重力和物体初、末位置所在水平面的高度差决定,即:![]() 。所以重力做的功等于重力势能增量的负值,即
。所以重力做的功等于重力势能增量的负值,即![]()
例4:如图5所示,半径为r,质量不计的圆盘面与地面相垂直,圆心处有一个垂直于盘面的光滑水平固定轴O,在盘的最右边缘,固定一个质量为m的小球A,在O点正下方离O点![]() 处,固定一个质量也为m的小球B,放开盘,让其自由转动,试计算:
处,固定一个质量也为m的小球B,放开盘,让其自由转动,试计算:
(1)当A球转到最低点时,两球的重力势能之和少了多少?
(2)A球转到最低点时的线速度是多少?
(3)在转动过程中,半径OA向左偏离竖直方向的最大角度是多少?
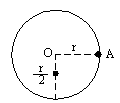
图5
析与解:
(1)重力势能之和减少了:![]()
(2)![]() ,
,![]()
(3)![]() ,即
,即![]()
解得:![]()
点评:两球速度不同,搞清速度关系是本题解题的关键。
(五)对机械能守恒条件的认识
如果没有摩擦力和介质阻力,物体只发生动能和势能的相互转化时,机械能的总量保持不变,这就是机械能守恒定律。没有摩擦和介质阻力,这是守恒条件。具体的讲,如果一个物理过程只有重力做功,只是重力势能和动能之间发生相互转化,没有与其他形式的能发生转化,物体的动能和重力势能总和保持不变。如果只有弹簧的弹力做功,在弹簧与物体系统中就只有弹性势能与动能之间发生相互转化,不与其他形式的能发生转化,所以弹性势能和动能总和保持不变。分析一个物理过程是不是满足机械能守恒,关键是分析这一过程中有哪些力参与了做功,这一力做功是什么形式的能转化成什么形式的能,如果只是动能和势能的相互转化,而没有与其他形式的能发生转化,则机械能总和不变。如果没有力做功,不发生能的转化,机械能当然也不发生变化。
例5:如图6所示,一质量为![]() 的半圆形槽内壁光滑,放在光滑的水平面上,槽的左侧有一固定的木桩以阻止槽水平向左运动,槽的半径为R。今从槽左侧A端的正上方D处有一个质量为
的半圆形槽内壁光滑,放在光滑的水平面上,槽的左侧有一固定的木桩以阻止槽水平向左运动,槽的半径为R。今从槽左侧A端的正上方D处有一个质量为![]() 的小球,球恰好从A点自由进入槽的内壁轨道。为了使小球沿槽的内壁恰好运动到槽的右端B点。试求D至A点的高度。
的小球,球恰好从A点自由进入槽的内壁轨道。为了使小球沿槽的内壁恰好运动到槽的右端B点。试求D至A点的高度。
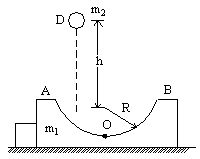
图6
析与解:此题若用常规法解答,复杂耗时且易出错。若构建能流图,利用整个过程机械能守恒,系统水平方向动量守恒,则易解此题,小球从D点落到O点再运动到B点,其能流图如下:
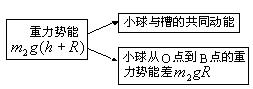
依题意有:![]() ①
①
![]() ②
②
![]() ③
③
联立①、②、③得:![]()
解之得:![]()
点评:掌握好机械能守恒的条件,利用能量流动图直观地分析物理过程是解答此题的关键。
【模拟试题】
1. 下列四个选项的图中,木块均在固定的斜面上运动,其中图A、B、C中的斜面是光滑的,图D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示。图A、B、D中的木块向下运动,图C中的木块向上运动,在这四个图所示的运动过程中机械能守恒的是( )
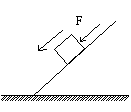
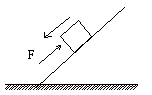
A B
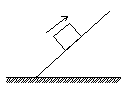
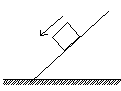
C D
图1
2. 1999年10月31日,山东青年燕庆伟在济南杨庄险段蛇口处骑自行车飞越黄河,他沿长100m,起点到最高点高度差为40m的搭建跑道,从静止开始加速到脱离跑道端点时,速度达到![]() ,则他消耗的能量至少约为( )
,则他消耗的能量至少约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 行驶中的汽车制动后滑行一段距离,最后停下;流星在夜空中坠落并发出明亮的火焰;降落伞在空中匀速下降。上述不同现象中所包含的相同的物理过程是( )
A. 物体克服阻力做功
B. 物体的动能转化为其他形式的能量
C. 物体的势能转化为其他形式的能量
D. 物体的机械能转化为其他形式的能量
4. 用铁锤把小铁钉敲入木板。假设木板对铁钉的阻力与铁钉进入木板的深度成正比。已知第一次将铁钉敲入木板1cm,如果铁锤第二次敲铁钉的速度变化与第一次完全相同,则第二次铁钉进入木板的深度是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 如图2所示是健身用的“跑步机”示意图,质量为m的运动员踩在与水平面成![]() 角的静止皮带上,运动员用力后蹬皮带,皮带运动过程中受到阻力恒定为
角的静止皮带上,运动员用力后蹬皮带,皮带运动过程中受到阻力恒定为![]() ,使皮带以速度
,使皮带以速度![]() 匀速运动,则在运动过程中下列说法正确的是( )
匀速运动,则在运动过程中下列说法正确的是( )
A. 人脚对皮带的摩擦力是皮带运动的阻力
B. 人对皮带不做功
C. 人对皮带做功的功率为![]()
D. 人对皮带做功的功率为![]()
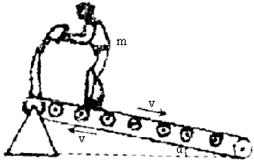
图2
6. 随着能源消耗增加,如何有效地提高能量利用率是人类所面临的一项重要任务。如图3所示是上海“明珠线”某轻轨列车车站的设计方案,与站台连接的轨道有一个小的坡度,列车进站时利用自身动能转化成 能,可以使列车很快停下来,出站时该能量又可以转化成列车的动能,从而起到节能作用。
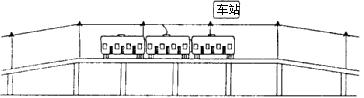
图3
7. 如图4所示,一缆车系统将乘客送上和送下高40m,长80m的山坡,整个系统由一上一下两个车厢组成,它们通过山顶一个巨大的滑轮由钢索相连,滑轮由电动机驱动,设每个车厢运动中受到摩擦力恒为![]() ,则整个缆车系统在一次全行程中克服摩擦力做功是 J。
,则整个缆车系统在一次全行程中克服摩擦力做功是 J。
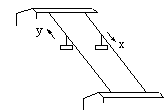
图4
8. 汽车的质量为![]() ,额定功率为30kW,运动中阻力大小为车重的0.1倍。汽车在水平路面上从静止开始以
,额定功率为30kW,运动中阻力大小为车重的0.1倍。汽车在水平路面上从静止开始以![]() 的牵引力出发,求:
的牵引力出发,求:
(1)经过多长的时间汽车达到额定功率;
(2)汽车达到额定功率后保持功率不变,运动中最大速度多大?
(3)汽车加速度为![]() 时速度多大?
时速度多大?
9. 如图5所示,一滑块由静止开始沿半径为R的光滑四分之一圆弧面的顶端A由静止滑下,A与圆心O在同一水平面上,经B点后进入粗糙水平地面,若滑块与地面间的动摩擦因数为![]() ,试求:① 滑块到达B点的速度;②
滑块在水平地面上能滑行的距离。
,试求:① 滑块到达B点的速度;②
滑块在水平地面上能滑行的距离。
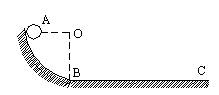
图5
【试题答案】
1.
C 2. B 3. A 4. B 5. D 6. 势能 7. ![]()
8.
(1)![]() (2)
(2)![]() (3)
(3)![]()
9.
(1)![]() (2)
(2)![]()