万有引力定律检测题
班级： ___________ 姓名：_________ 成绩：___________
一、选择题（本题包括10小题，每小题3分，共计30分。每小题只有一个或多个选项符合题意，选错或不答得0分，选不全得2分。）
1．设想人类开发月球，不断把月球上的矿藏搬运到地球上，假定经过长时间开采后，地球仍可看做是均匀的球体，月球仍沿开采前的圆周轨道运动．则与开采前相比 （ ）
A．地球与月球的万有引力将变大 B．地球与月球的万有引力将变小
C．月球绕地球运动的周期将变长 D．月球绕地球运动的周期将变短
2．人造地球卫星在环形轨道上绕地球运转，它的轨道半径、周期和环绕速度的关系是（ ）
A．半径越小，速度越小，周期越小 B．半径越小，速度越大，周期越小
C．半径越大，速度越大，周期越小 D．半径越大，速度越小，周期越小
3．一艘宇宙飞船贴近一恒星表面飞行，测得它匀速圆周运动的周期为T，设万有引力常数G，则此恒星的平均密度为： （ ）
A．GT2/3π B．3π/GT2
C．GT2/4π D．4π/ GT2
4．有关人造地球卫星的说法中正确的是： （ ）
A．第一宇宙速度是卫星绕地球运行的最小速度
B．第一宇宙速度是近地圆轨道上人造卫星运行速度
C．第一宇宙速度是能使卫星进入近地圆形轨道的最小发射速度
D．卫星环绕地球的角速度与地球半径R成反比
5．宇宙飞船要与环绕地球运转的轨道空间站对接，飞船为了追上轨道空间站 （ ）
A．只能从较高轨道上加速 B．只能从较低轨道上加速
C．只能从与空间站同一轨道上加速 D．无论在什么轨道，只要加速即可
6．已知引力常数G与下列哪些数据，可以计算出地球密度： （ ）
A．地球绕太阳运动的周期及地球离太阳的距离
B．月球绕地球运行的周期及月球绕地球转的轨道半径
C．人造地球卫星在地面附近绕行运行周期
D．若不考虑地球自转，已知地球半径和重力加速度
7．同步卫星相对地面静止，尤如悬在高空中，下列说法中正确的是： （ ）
A．同步卫星可能处于不同的轨道上 B．同步卫星的速率是唯一的
C．同步卫星加速度大小是唯一的 D．各国的同步卫星都在同一圆周上运行
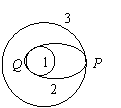8．发射地球同步卫星时，先将卫星发射到近地圆轨道1，然后点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步圆轨道3。轨道1、2相切于Q点，轨道2、3相切于P点，如图所示，则当卫星分别在1、2、3轨道上正常运行时，下列说法中正确的是：（ ）
A、卫星在轨道3上的速率大于在轨道1上的速率
B、卫星在轨道3上的角速度小于在轨道1上的角速度
C、卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度
D、卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度
9．地球同步卫星到地心的距离r可由r3=
求出.已知式中a的单位是m，b的单位是s，c的单位是m/s2，则 （ ）
A．a是地球半径，b是地球自转的周期，c是地球表面处的重力加速度
B．a是地球半径，b是同步卫星绕地心运动的周期，c是同步卫星的加速度
C．a是赤道周长，b是地球自转的周期，c是同步卫星的加速度
D．a是地球半径，b是同步卫星绕地心运动的周期，c是地球表面处的重力加速度
10．2003年8月29日，火星、地球和太阳处于三点一线，上演“火星冲日”的天象奇观．这是6
万年来火星距地球最近的一次，与地球之间的距离只有5576万公里，为人类研究火星提供
了最佳时机．图示为美国宇航局最新公布的“火星大冲”
的虚拟图．则有（ ）
A．2003年8月29日，火星的线速度大于地球的线速度
B．2003年8月29日，火星的线速度小于地球的线速度
C．2004年8月29日，火星又回到了该位置
D．2004年8月29日，火星还没有回到该位置
二、填空题（本题包括5小题。每空4分，共计24分）
11．设在地球上和某天体上以相同的初速度竖直上抛一物体的最大高度之比为k（均不计阻力），且已知地球与该天体的半径之比也为k，则地球与天体的质量比为_______ 。
12．某物体在地球表面上受到的重力为160 N；将它放置在卫星中，在卫星以加速度a=g/2随火
箭加速上升的过程中，当物体与卫星中的支持物的相互挤压力为90 N，卫星此时距地面的高度为
_______.（已知地球的半径R=6.4×103 km，取g=10 m/s2）
13.天文学家根据天文观测宣布了下列研究成果：银河系中可能存在一个大“黑洞”，接近“黑洞”的
所有物质，即使速度等于光速也被“黑洞”吸入，任何物体都无法离开“黑洞”.距离“黑洞”r=6.0×1012
m的星体以v=2×106 m/s的速度绕其旋转，则黑洞的质量为_______.
(引力常G=6.67×10-11N·m2/kg2.)
14.一颗以华人物理学家“吴健雄”命名的小行星，半径约为16 km，密度与地球相近.若在此小行星
上发射一颗绕其表面运行的人造卫星，它的发射速度约为___________.（已知地球的半R=6.4×103
km，取g=10 m/s2）
15两颗人造地球卫星A.B绕地球作圆周运动,周期之比为T1 :T2 =1:8,则A.B的轨道半径之比和运动速率之比分别为___________.和___________.。
三、计算题（本题包括4小题，共计46分。解答应写出必要的文字说明、方程式和重要演算步骤．只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数值和单位。）
16．某星球中心离地球中心的距离是地球半径的60倍，其质量约是地球质量的1/81，当飞船飞到该星球和地球中心连线上距地球中心多远时，它受到该星球引力跟地球引力刚好相等？已知地球的半径为R。（10）
17．宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时的初速增大到2倍，则抛出点与落地点之间的距离为
L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。（12）
18．两颗卫星在同一轨道平面绕地球做匀速圆周运动，地球半径为R，a卫星离地面的高度等于R，b卫星离地面高度为3R，则（12）
（1）a、b两卫星周期之比Ta∶Tb是多少?
（2）若某时刻两卫星正好同时通过地面同一点的正上方，则a至少经过多少个周期两卫星相距最远?
19．2005年10月12日9时，“神舟”六号飞船一飞冲天，一举成功，再次把中国人“巡天遥看一天河”的陆地梦想变成“手可摘星辰，揽明月”的太空现实，“神舟”六号飞船点火发射时，飞船处于一个加速过程，在加速过程中宇航员处于超重状态。人们把这种状态下宇航员所受支持力FN与在地表面时重力mg的比值
称为载荷值。（12）
（1）假设宇航员聂海胜和费俊龙在超重状态下载荷值的最大值为K=7，飞船带着宇航员竖直向上发射时的加速度a的最大值为多少？已知地球表面的重力加速度g=10m/s2。
（2）“神舟”六号飞船发射成功后，进入圆形轨道稳定运行，运转一圈的时间为T，地球的半径为R，表面的重力加速度为g，万有引力常量为G，试求这一圆形轨道距离地面的高度H。（用R、g、T、G表示）
万有引力测试答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | BD | B | B | BC | B | BCD | BCD | BD | AD | BD |
二、填空题
11． k
12．19.2×103 km
13．3.6×1035
14．20 m/s
15 1:4 2:1．
三、计算题
16.设星球的质量为m1 月球的质量为m2 飞船的质量为m ,飞船距地球中心的距离为r
由万有引力定律公式
3
可知：G
=G
4
又由 
解得： r=54R 3
17．解：设抛出点的高度为h，第一次平抛的水平射程
为x，则有 x2+h2=L2 ① 2
由平抛运动规律得知，当初速增大到2倍，其水平
射程也增大到2x，可得
(2x)2+h2=(
由①、②解得 h=L/
设该星球上的重力加速度为g，由平抛运动的规律，
得 h=gt2/2 2
由万有引力定律与牛顿第二定律，得 GMm/R2=mg 2
式中m为小球的质量，联立以上各式，解得
M=2
18. （1）由卫星运动规律知:Ta∶Tb＝
∶
＝1∶2
4
（2）Ta＜Tb，当二者相距最远时，即a比b多转半圈，即
＝0.5
6
解得t＝
0.77Ta
2
2
19.由牛顿第二定律可知： FN－mg=ma (1)
又由
K=
(2)
将（2）式代入（1）式可得：
mg(k-1)=ma (3)
将k=7代入（3）式
可得： a=60m/s2
(2)(6分)
设地球的质量为 M ，飞船的质量为m ，飞船距地面高为h
万有引力充当向心力：
G
（1）
在地球表面附近: G
=mg （2）
由（1）（2）联立可解: h=
-R
(3)