高一物理第一学期期中考试试题
（尖子班用）
一、选择题：本题共10小题，每小题4分，在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。全部选对的得4分，选不全的得2分，有选错或不答的得0分.
1．物体做平抛运动时，它的速度方向与水平方向的夹角的正切tanα随时间t变化的图象是（ ）
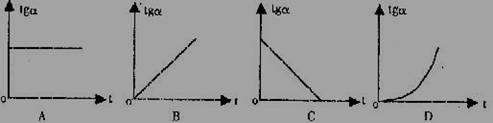
2．关于运动的合成和分解，下述说法中正确的是 （ ）
A．合运动的速度大小等于分运动的速度大小之和
B．物体的两个分运动若是直线运动，则它的合运动一定是直线运动
C．合运动和分运动具有同时性
D．若合运动是曲线运动，则其分运动中至少有一个是曲线运动
3．下列说法正确的是 （ ）
A．运动物体在某一时刻的速度可能很大而加速度不可能为零
B．运动物体在某一时刻的速度可能为零而加速度可能不为零
C．在初速度为正、加速度为负的匀变速直线运动中，速度可能增大
D．初速度为正、加速度为正的匀变速直线运动中，当加速度减小时，它的速度也减小
| |
A． FN 、Ff和T都增大 B．FN、Ff增大，T不变
C． FN 、Ff和T都减小 D．FN增大，Ff减小，T不变
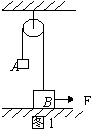
5．如图2，在光滑水平面上放着紧靠在一起的AB两物体，B的质量是A的2倍，B受到向右的恒力ＦB=2N，A受到的水平力ＦA=(9-2t )N。从t＝0开始计时，则下列说法中正确的是 （ ）
A．A物体在3秒末时刻的加速度是初始时刻的5/11倍
B．t＞4秒后，B物体做匀加速直线运动
C．t = 4.5秒时， A物体的速度为零
D．t＞4.5秒后， AB的加速度方向相反
6．一物体以初速度v由地面竖直向上抛出。如果物体运动时受到空气阻力大小不变，图3中能基本反映出它的速度变化和时间关系的是 （ ）
 |
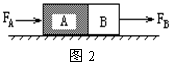
7．如图4所示，物体B放在物体A上，A、B的上下表面均与斜面平行，当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时 （ ）
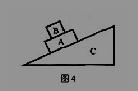A．A受到B的摩擦力沿斜面方向向上
B．A受到B的摩擦力沿斜面方向向下
C．A、B之间的摩擦力为零
D．A、B之间是否存在摩擦力取决于A、B表面的性质
8．玻璃生产线上，宽8m的成型玻璃板以3m/s的速度连续不断地向前行进在切割工序处，金钢钻割刀速度为5m/s，割下的玻璃板都成规定尺寸的矩形。金刚钻割刀切割完一块后，立即复位，紧接着切割第二块。复位时间忽略不计，则 （ ）
A．切割一次时间为1.6S
B．金钢钻割刀应沿垂直玻璃板运动方向进行切割
C．切割一次时间为2S
D．切割出的矩形玻璃板的尺寸规格都为8m×6m
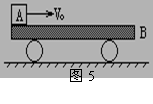9．小平板车B静止在光滑水平面上，物体A以某一水平初速度v0滑向B的一如图5所示，由于A、B间存在摩擦，因而A滑上B后， A开始作减速运动，B开始作加速运动，设B足够长，则B速度达到最大时，下列说法正确的是 （
）
A．A在B上停止滑动时 B．A、B速度相等时
C．A的速度为零时 D．A、B开始作匀速直线运动时
10．如图所示，用AO、BO两根细线吊着一个重物P，AO与天花板的夹角θ保持不变，用手拉着BO线由水平逆时针的方向逐渐转向竖直向上的方向，在此过程中， BO和AO中张力的大小变化情况是：（ ）
A、都逐渐变大 B、都逐渐变小
C、BO中张力逐渐变大，AO中张力逐渐变小
D、BO中张力先变小后变大，AO中张力逐渐减小到零
二、非选择题：解答应写出必要的文字说明、方程式和重要的演算步骤，有数值计算的题，答案中必须写出数值的单位。
11．（5分）为探究钢球的液体中运动时受阻力的大小，让钢球从某一
高度竖直落下进入液体中运动，用闪光照相方法拍摄钢球在不同时刻
的位置，如图所示．已知钢球在液体中运动时所受阻力F=kv2，闪光
照相机的闪光频率为f，图中刻度尺的最小分度为s0，钢球的质量为
m，则阻力常数k的表达式为__________.（重力加速度为g）
12（16分）．利用打点计时器《探究小车的速度随时间变化的规律》，如图给出了该次实验中，从0点开始，每5个点取一个计数点的纸带，其中1、2、3、4、5、6都为记数点。测得：s1=1.40cm，s2=1.90cm，s3=2.40cm，s4=2.90cm，s5=3.40cm，s6=3.90cm。
（1）在计时器打出点2、3、4、5、时，小车的速度分别为：v2= cm/s，v3= cm/s，v4= cm/s，v5= cm/。
（2）在右边的坐标纸上作出速度—时间图象(从1开始计时)。
（3）小车的加速度为 m/s2（取二位有效数字）。
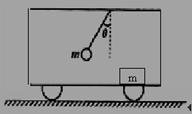
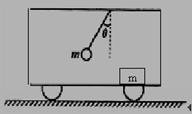
13．如图所示，车厢在水平路面上做直线运动，车厢内系住小球的悬线偏离竖直方向的夹角恒为θ，车厢地板上放置一质量为m的木箱，它与车厢之间无相对滑动．
（1）试分析说明小车的运动情况；
（2）求木箱受到的摩擦力大小和方向．
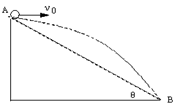
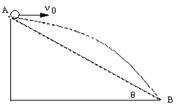14．如图所示从倾角为θ的斜面上的A点以速度V0平抛一个小球，小球刚好落在斜面上的的最低点B处。求：（1）经多长时间落到斜面上的B点？（2）落到B点时的速度大小？
15．为了测量一高楼的高度，有人设计了如下实验：在一根长为l的绳两端各拴一重球，一人站在楼顶上，手执绳的上端使小球与楼顶平齐并无初速释放，使其自由下落，另一个人在楼下测量两球落地的时间差△t，即可根据l、△t、g得出楼的高度（不计空气阻力）．从原理上讲，这个方案是否正确？若测得l=10m，△t=0.4s，g=10m/s2，试估算楼的高度．
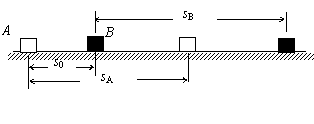
16．如图所示，A、B两物体在同一直线上运动，当它们相距 s0＝7m时，A在水平拉力和摩擦力的作用下，正以vA＝ 4m/s的速度向右做匀速运动，而物体B此时速度vB＝10m/s向右，以a＝－2m/s2的加速度做匀减速运动，则经过
多长时间A追上B?若vA＝8m/s ，则又经多长时间A追上B？
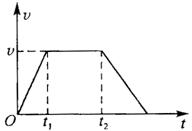
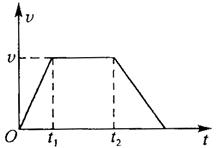17．一位同学的家住在一座25层的高楼内，他每天乘电梯上楼，经过多次仔细观察和反复测量，他发现电梯启动后的运动速度符合如图所示的规律，他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内，将重物放在台秤的托盘上，电梯从第一层开始启动，经过不间断地运行，最后停在最高层.在整个过程中，他记录了台秤的不同时间段内的示数，记录的数据如下表所示.但由于0—3.0s段的时间太短，他没有来得及将台秤的示数记录下来.假设在每个时间段内台秤的示数是稳定的，重力加速度g取10m/s2.
| 时间/s | 电梯启动前 | 0—3.0 | 3.0—13.0 | 13.0—19.0 | 19.0以后 |
| 台秤示数/kg | 5.0 | 5.0 | 4.6 | 5.0 |
(1)电梯在0—3.0s时间段内台秤的示数应该是多少？
(2)根据测量的数据，计算该座楼房内每一层的平均高度.
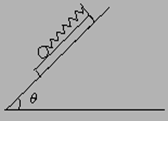
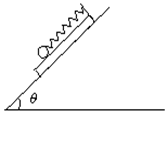18.为了测量小木板和斜面间的动摩擦因数，某同学设计了如下实验.在小木板上固定一个弹簧秤(弹簧秤的质量可以忽略不计)，弹簧秤下吊一个光滑小球，将木板连同小球一起放在斜面上，如图所示，用手固定住木板时，弹簧秤的示数为F１，放手后木板沿斜面下滑，稳定时弹簧秤的示数是F２，测得斜面倾角为θ.由测量的数据可以计算出小木板与斜面间的动摩擦因数是多少?
  |
| |||
高一物理（尖子班用）
一、选择题答案涂在答题卡上（答在其它地方无效）
二、非选择题：解答应写出必要的文字说明、方程式和重要的演算步骤，有数值计算的题，答案中必须写出数值的单位。
11、（5分） 。
12、（16分）
（1）、① ② ；
③ ④ 。
（2）在右图中作出图线
（3） 。
13、（13分）
14、（13分）
15、（14分）
16、（15分）
17、（17分）
| 时间/s | 电梯启动前 | 0—3.0 | 3.0—13.0 | 13.0—19.0 | 19.0以后 |
| 台秤示数/kg | 5.0 | 5.0 | 4.6 | 5.0 |
18、（17分）
参考答案：
1．D 2．C 3．BC 4．B 5．ABD 6．B 7．C 8．CD 9．ABD 10．D
11．
（5分）
12．（1）v2= 16.50 cm/s，v3= 21.50 cm/s，v4= 26.50 cm/s，v5=31.50 cm/。（每空2分） （2）作图正确（4分） （3）0.50 m/s2（4分）
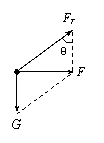13．解：（1）设小球质量为m0，其受力情况如图所示，
则
．
根据牛顿第二定律，有
．
联立解得a=g tgθ 为一定值．
所以，车厢可能向右做匀加速直线运动，亦可能向左做匀减速直线运动．
（2）对木箱，由牛顿第二定律可得Ff=ma=mgtgθ，方向水平向右．
14．（1）
（2）
15．解：从原理上讲，这个方案是正确的．
根据自由落体运动的规律，有
联立消去t解得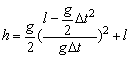
代入数据得h=36.45m．
16．（15分）先判断A追上B时，是在B停止运动前还是后。
B匀减速到停止的时间为：t0＝
＝5s
在5s内A运动的位移：sA ＝vAt0＝20m
在5秒内B运动的位移：sB ＝vBt0 ＋ 
＝25m
因为：sA＜sB＋s0，即：B停止运动时，A还没有追上B。
A追上B的时间为：t＝t0 ＋
＝8s
若vA＝8m/s，则A在5s内运动的位移为：sA＝ vAt0＝40m
因为：sA＞sB＋s0 ，即：B停止运动前，A已经追上B。
则：
t＇＝（1＋2
）s＝3.82s
17．解：（1）依题意可知：重物的质量m=5.0kg
设电梯运动中的最大速度为v，加速阶段和减速阶段的加速度分别为a1和a3，
则v=a1△t1=a3△t3
又加速阶段有：F1－mg=ma1
减速阶段有：mg－F3=ma3
F3=4.6×10N=46N．
由以上各式解得F1=58N，则台秤示数应为5.8kg．
（2）19.0s内电梯上升的高度
m
该楼房每层楼的平均高度
m=2.9m
18．
μ＝
ｔａｎθ