直线运动规律及其应用

一、　　　　 匀变速直线运动的基本公式

匀变速直线运动的加速度a 是恒定的. 反之也成立. 加速度方向与初速度方向相同的匀变速直线运运称为匀加速直线运动; 加速度的方向与初速度方向相反叫匀减速直线运动.

如果以初速度v₀的方向为正方向，则在匀减速直线运动中，加速度应加一负号表示。

2. 基本规律: (公式)

(1)　  速度公式:  v_t= v₀ + a t 　或：a = .　(图象为一直线,纵轴截距等于初速度大小)

(2)　  位移公式:　s = v₀t + at²

　　注：在v－t图象中，由v－ t 直线与两坐标轴所围的面积等于质点在时间t内运动的位移

(3). 推论:　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

(3)　  平均速度:　 =　S / t （前一式子只适用于匀变速直线运动，它是指平均速度，不是速度的平均值；后一式子对任何变速运动均适用。

说明: 以上各矢量均自带符号,与正方向相同时取正,相反取负.在牵涉各量有不同方向时,一定　　　　　　　　　　　　　　

要先规定正方向. 如果物体做匀加速直线运动时加速度取正值的话,则匀减速直线运动时加速度就取负值代入公式运算. 对做匀减速直线运动的情况,一般要先判断物体经历多少时间停止下来,然后才能进行有关计算.否则可能解出的结果不符合题意.

例如，一个质点先以加速度a₁从静止开始做匀加速直线运动，经时间t ，突然加速度变为反方向，且大小也发生改变，再经相同时间，质点恰好回到原出发点。试分析两段时间内的加速度大小关系，以及两段时间的末速度大小关系。

例1.一颗子弹水平射入静止在光滑水平面上的木块中. 已知子弹的初速度为v₀ , 射入木块深度为L后与木块相对静止,以共同速度v 运动,求子弹从进入木块到与木块相对静止的过程中,木块滑行的距离.

例2. 一列火车从静止开始做匀加速直线运动, 一个人站在第1节车厢的前头观察,第1节车厢通过他用了1s ,全部列车通过他用了6s钟, 则这列火车共有多少节车厢?

例3. 两辆完全相同的汽车,沿水平直路一前一后匀速行驶,速度为v₀ .若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车时的加速度开始刹车. 已知前车在刹车过程中行驶的距离为s ,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为:

A.  s ;　　B. 2s ;　　C. 3s ;　　D 4s .

例4. 羚羊从静止开始奔跑,经过50m距离加速到最大速度25m/s,并能维持一段较长时间;猎豹从静止开始奔跑经过60m的距离能加速到最大速度30m/s,以后只能维持这个速度4.0s.设猎豹距离羚羊x m时开始攻击,羚羊在猎豹开始攻击后1.0s才开始奔跑,假定羚羊和猎豹加速阶段分别做匀加速运动,且均沿同一直线索奔跑.求:⑴猎豹要在其最大速度减速前追到羚羊,x值应在什么范围? ⑵猎豹要在其加速阶段追上羚羊, x值应在什么范围?

例5 天文观察表明:　几乎所有远处的恒星(或星系)都在以各自的速度背离我们而运动,离我们越远的星体,背离我们的速度(称为退行速度)越大; 也就是说,宇宙在膨胀,不同的星体的退行速度v和它们离我们的距离r成正比,即: v = H r. 式中的H为常数,称为哈勃常数, 已由天文观测测定. 为解释上述现象,有人提出一种理论认为宇宙是从一个爆炸的火球开始形成的. 假设爆炸后各星体即以不同的速度向外匀速运动,并设想我们就位其中心. 则速度越大的星体现在离我们越远.这一结果与上述天文观测一致.

由上述理论和天文观测结果,可估算宇宙年龄T , 其计算式为T = _________. 根据近期观测,哈勃常数H =3×10^－2米/秒•光年.其中光年是光在一年中进行的距离,由此估算宇宙年龄为_______年.

例6.（追击问题中的极值问题） 一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s²的加速度开始行驶,恰在这时一辆自行车以6m/s的速匀速驶来,从后边赶过汽车.试求 :

(1)　  汽车从路口开动后,在追上自行车之前经过多长时间两车最远? 最远距离是多少? 此时汽车的速度是多大?

(2)　  什么时候汽车追上自行车, 此时汽车的速度是多少

例7.（临界法） 火车以速度v₁在轨道上向前匀速行驶,司机突然发现前方同轨道上相距s处另一列火车正以较小的速度v₂匀速行驶且并未发现自已的火车.司机即以某一加速度紧急刹车.为使两车避免相撞, 加速度a应满足什么条件?

二、匀变速直线运动的三个推论（普适性）

1.　　　 任意两个连续相等时间间隔(T)内的位移之差为一恒量.即:

S₂－S₁ = S₃－S₂ = S₄－S₃ = …… = S_N－S_N－1 = aT²

2.　　　 在一段时间的中间时刻的瞬时速度v_t/2 = ( v₀ + v_t )/ 2 = s/ t

3.　　　 做匀变速直线运动的质点经时间通过位移为s, 则中间时刻的瞬时速度总小于位移中点　　　　　　　　　　　　　　　　　 

的瞬时速度.不论是匀加速还是匀减速直线运动. 即v _t/2 < v_s/2　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　

三、 初速度为零的匀加速直线运动的特点

1.　　　 1T末, 2T末, 3T末, … n T末瞬时速度之比为:

v₁ ∶v₂∶ v₃ ∶…:∶v _n = 1∶2 ∶3 ∶… ∶n .

(2)  1T内, 2T内, 3T内， … n T内位移之比为:

s₁ ∶s₂ ∶ s₃ ∶… ∶s _n = 1² ∶ 2² ∶3²∶…∶n² .

(3). 第一个T内, 第二个T内， 第三个T内， …, 第n个T内位移之比为.

 S ₁ ∶s₂∶s₃∶… = 1∶3∶5 ∶… ∶(2n－1).

(4). 通过连续相等的位移所用的时间之比为:

 t₁ ∶t₂ ∶t₃ ∶ … ∶ t_n = 1∶… ∶ ().

例8. 一物体从斜面上某点由静止开始做匀加速直线运动,经过3秒后到达斜面底端,并开始在　　　　　　　　　　　　　　　　 

水平地面上做匀减速直线运动,又经9秒停止. 则物体在斜面上的位移与在水平地面上的位移之比是:　 A. 1∶1;　　B. 1∶2 ;　 C. 1 ∶3 ;　 D. 3∶1 .

例9. 三块完全相同的木块固定在地板上. 一初速度为v₀的子弹水平射穿第三块木板后速度恰好为零. 设子弹在三块木板中的加速度相同,求子弹分别通过三块木板的时间之比.

例10. 一质点由A点出发沿直线AB运动,行程的第一部分是加速度为a₁的匀加速运动,接着做加速度为a₂的匀减速运动,到达B点时恰好速度减为零. 若AB间总长度为S ,试求质点从A到B所用的时间 t.

例11. 某人骑自行车以.4m/s的速度匀速前进, 某时刻在他前面7m处以10m/s的速度同向行驶的汽车开始关闭发动机,而以2m/s²的加速度匀减速前进,此人需多长时间才能追上汽车?

例12. 摩托车从静止开始以a₁ =1.6m/s²的加速度沿直线匀加速行驶,中途做了一段匀速运动,后以a₂ = 6.4m/s²的加速度做匀减速运动,直到停止,一共经历了130s ,总位移是1.6 ×10³m. 求:

(1) 摩托车的最大速度?　 (2) 在起动和减速的加速度跟(1)相同的条件下, 摩托车在这段位移中如何运动所需时间最短,且此种情况的最大速度?

四、 自由落体运动和竖直上抛运动

1、自由落体运动的条件: ① 初速度为零;　② 只受重力作用.（ 平时物体在空中向下运动,如果　　　　　　　　　　　　　　　 

空气阻力跟物体所受的重力相比可忽略时,可视为自由落体运动.）

自由落体运动是一种初速度为零的匀加速直线运动.在地面附近取 g =9.8 m/s².

自由落体运动公式: v_t = gt ,  h =t² ,  = 2 gh .　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

例1. 物体自某高度自由下落,最后1s内下落的高度是总高度的7/16, 取重力加速度 g = 9.8m/s², 求物体下落的总高度和总时间,

例2. 物体自A点自由下落,经过B点到达C点,已知物体经过B点时的速度是到达C点时速度的3/5, BC间距离为8m ,求AB间距离和到达C点时的速度.　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　 

2. 竖直上抛运动.

(1).物体做竖直上抛运动的条件: ①物体具有竖直向上的初速度; ② 物体只受重力作用.

(2) 竖直上抛运动规律:

①　　 上升过程: 物体做匀减速直线运动, 当末速度v =0时,物体到达最高点.以向上为正方向,则　　　　　　　　　　

v_t = v₀－gt　 h = v₀t － g t² /2 ;　v_t²－v₀² = －2gh ( h 为以抛出点为起点的位移.)

②　　 下降过程:　物体做自由落体运动.

③. 几个重要的物理量: 最大高度　H = v₀² /2g　总时间 t =2v₀/ g.　　　　　　　　　　　　　　　　　　　　　　　

④ 两个重要关系:　t_上 = t_下= v₀/g .(时间的对称性).

 在抛出点上方任一位置A: 上升速度与下落速度等值反向 v_A = －v_Aˊ

⑤ 表达式 h = v₀ t － 中h 的符号规定: 在抛出点上方时h取正, 在抛出点下方取负.　　　　　　　　　　　 　　　

在抛出点上方时, 同一个h对应两个t的值.在抛出点下方. 则只有一个t 的值.

五、本章常用的解题方法有：逐差法、图象法、极限分析法，对称原理、相对运动观点、相似大角形性质、自由弦的等时性、整体法、逆向思维法。

例3.（整体法） 气球上系一重物,以4m/s的速度匀速上升,当离地面高9m时绳子断了,求: ①重物经过多长间落回地面? ②重物落地时的速度多大? 取g =10m/s²

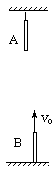例4.（相对运动观点） 如图所示. A, B两棒长度均为1m, A悬挂于高处. B竖直立于A下面的地面上,A的下端和B的上端相距20m , A 做自由落体运动, B同时以初速度40m/s , 竖直上抛,在运动过程中两棒都保持竖直,问: ① 两棒何时开始相遇(不相碰); ② 从相遇到分离历时多少? 取 g=10m/s².

练习:（相对运动） 1. 有一台电梯的天花板与底板间的距离为2.5m ,它从静止开始以加速度a =10 m/s²竖直向上加速度运动, 同时天花板上有一颗螺丝钉从脱落到底板上共需多长时间? ( g =10m/s² )

2.从离地H高处自由下落一个小球, 同时在地面上正对着这个小球以初速度v₀竖直上抛出另一个小球, 要使两球在离地2H/ 3 处相遇, 第二个小球的初速度v₀应为多大? .

3. (1999年全国高考题) （理想模型）一跳水运动员从离地面10m高的平台上向上跳起, 举双臂直体离开台面,此时重心位于从手到脚全长的中心，跃起后重心升高0.45m 达到最高点, 落水时身体竖直, 手先入水(在此过程中运动员水平方向的运动忽略不计)，从离开跳台到手触水面, 他可用于完成空中动作的时间是______s ,(计算时, 可以把运动员看作全部质点集中在重心的一个质点, g取10m/s² ,结果只保留两位有效数字.

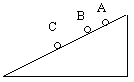4. 有若干相同的小钢球,从斜面上的某一位置每隔0.1s无初速地释放一颗, 在连续释放若干颗钢球后,对准斜面上正在滚动的若干小球拍摄到如右图所示的照片,测得AB =15cm , BC =20cm. 求: （逐差法）　　　　　　　　　　　　　

①　　 拍摄照片时B球的速度; ② A球上面还有几颗正在滚动的小钢球.

5. 某种类型的飞机起飞时,从静止开始做匀加速直线运动,加速度大小为4m/s² , 飞机速度达到80m/s时离开地面升空.如果在飞机达到起飞速度时,突然接到命令停止起飞,飞行员立即使飞机紧急制动,飞机做匀减速运动, 加速度的大小为5. 0m/s² , 请你为该类型飞机设计一条跑道,使在这种特殊的情况下飞机停止起飞而不滑出跑道, 你设计的跑道长度至少多长?（临界法）

6. 做匀变速直线运动的物体,在第1s内的平均速度比在第2s内的平均速度大2 m/s, 而位移小4m ,求物体运动的初速度和加速度各是多大?

7. 石块A自塔顶落下L (m)时, 石块B自塔顶下方n(m)处自由落下, 两石块同时落地, 则塔高为

A. L + n ;  B .(L+n)²/4L ;　C. L²/ 4(L+n);　 D. (L+n)² / (L－n).（分层表达，综合处理）

8.某人在高层楼房的阳台外侧上方以20m/s的速度竖直向上抛出一个石块, 石块运动到离抛出点15m处所经历的时间可以是: （分类讨论与整体法）

A. 1 s ;　B. 2s ;　 C. 3s ;　　 D. (+2)s .

9.在正常情况下, 火车以54km/h 的速度匀速开过一个小站。现因需要, 必须在这一小站停留, 火车将到小站时以－0.5m/s²的加速度做匀减速运动 停留2min后, 又以0.3m/s²的加速度出小站一直到恢复原来的速度. 求因列车停靠小站而延误的时间.

10. （对称性原理）子弹从枪口射出的速度大小是30m/s ,某人每隔1s竖直向上开一枪, 假定子弹在升降过程中都不相碰. 试求: ①空中最多能有几颗子弹? ②设在t=0时将第一颗子弹射出, 在哪些时刻它和以后射出的子弹在空中相遇而过? ③这些子弹在距枪口多高的地方依次与第一颗子弹相遇?(不空气阻力)

11、一个物体以初速度v₀ 在倾角为θ的斜面上运动，且与斜面的动摩擦因数为μ，则在同样条件下，物体沿斜面上滑与下滑的加速度之比：（极限分析法）

A. (sinθ－μcosθ)∶(cosθ－μsinθ);　 B.( sinθ+μcosθ)∶(sinθ－μcosθ)

C. (sinθ+μcosθ)∶cosθ　　　　　　  D. μcosθ∶(sinθ－μcosθ)

解：当斜面光滑时，μ=0 ，物体上滑与下滑的加速度相等，即：a_上∶a_下=1∶1。所以选B。

12、将一个小球竖直向上抛出，初速度与返回抛出点的末速度之比为k ,设小球运动中受到的空气阻力大小不变，则空气阻力f与小球重力（mg）之比为：

A.k ;　 B. 1/k ;　 C. (k²－1)∶(k²+1) ;　 D.  (k+1)∶(k－1).

分析：当k =1时，空气阻力f = 0, 则f /mg = 0. 所以，应选C。

13、（类比法与平均值处理）A、B两站相距S，将其分成n等份，汽车以加速度a从A出发，分段作匀加速直线运动，且到达每一等分末端时，加速度增加a/n , 求汽车到达B站的速度。

14、（图象法）A、B两站相距S，汽车从A站以恒定加速度a₁开出，最后又以恒定加速度a₂作匀减速运动，且正好在B站停下。为了使行车时间最短，汽车在中途应如何运动？最短时间是多少？最大速度是多少？

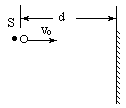15、（相似三角形性质）如图所示，在距离竖直墙壁为d处，有一个点光源，一个小球从s处以初速度v₀水平抛出。关于小球的影子在墙壁上的运动情况，下列哪些说法正确：

A、 影子作自由落体运动；B、影子作匀速直线运动；

C、小球初速度v₀减小，影子的速度增大；

D、点光源与墙壁的间距d 增大，影子的速度增大。

16、（自由弦的等时性）如图所示，直径为d的竖直圆环，一个光滑小环从

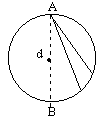静止开始，沿大圆环最高点A沿不同的弦运动到圆周上或者从圆周上沿不同的弦运动到圆环最低点B，所需时间都相同，且等于沿直径自由下落的时间，即 t =

17 、如图所示，一个物体沿有共同底边（L）的不同斜面，从顶部由静止开始无摩擦滑下，试证明：

沿倾角α= 45°的斜面滑下，所需时间最短，为 t_min = 2