第六章 曲线运动测试题
(时间 60分钟 满分 100分)
一、选择题(每小题5分,共50分)
1.关于曲线运动,下列说法正确的是 ( )
A.曲线运动不一定是变速运动
B.曲线运动可以是匀速率运动
C.做曲线运动的物体没有加速度
D.做曲线运动的物体加速度一定恒定不变
2.同一辆汽车以同样大小的速度先后开上平直的桥和凸形桥,在桥的中央处有 ( )
A.车对两种桥面的压力一样大 B.车对平直桥面的压力大
C.车对凸形桥面的压力大 D.无法判断
3.甲、乙两个物体分别放在广州和北京,它们随地球一起转动时,下面说法正确的是( )
A.甲的线速度大,乙的角速度小
B.甲的线速度大,乙的角速度大
C.甲和乙的线速度相等
D.甲和乙的角速度相等
4.做平抛运动的物体,每秒钟的速度增量是 ( )
A.大小相等,方向相同 B.大小不等,方向不同
C.大小相等,方向不同 D.大小不等,方向相同
5.水平抛出一个物体,经时间t后物体速度方向与水平方向夹角为θ,重力加速度为g,则平
抛物体的初速度为 ( )
A.gtsinθ B.gtcosθ C.gttanθ D.gtcotθ
6.关于圆周运动的下列说法中正确的是 ( )
A.做匀速圆周运动的物体,在任何相等的时间内通过的位移都相等
B.做匀速圆周运动的物体,在任何相等的时间内通过的路程都相等
C.做圆周运动的物体的加速度一定指向圆心
D.做圆周运动的物体的加速度不一定指向圆心
7.火车以某一速度v通过某弯道时,内、外轨道均不受侧压力作用,下面分析正确的是( )
A.轨道半径R=![]()
B.若火车速度大于v时,外轨将受到侧压力作用,其方向平行轨道平面向外
C.若火车速度小于v时,外轨将受到侧压力作用,其方向平行轨道平面向内
D.当火车质量改变时,安全速率也将改变
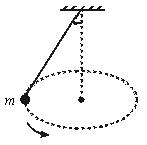 8.如图所示,用细绳系着一个小球,使小球在水平面内做匀速圆
8.如图所示,用细绳系着一个小球,使小球在水平面内做匀速圆
周运动,不计空气阻力,关于小球受力说法正确的是( )
A.只受重力
B.只受拉力
C.受重力、拉力和向心力
D.受重力和拉力
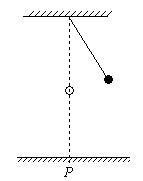
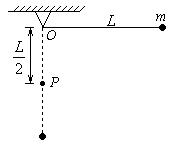 9.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的
9.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的
正下方![]() 处有一钉子P,把细线沿水平方向拉直,如图所示,
处有一钉子P,把细线沿水平方向拉直,如图所示,
无初速度地释放小球,当细线碰到钉子的瞬间,设线没有
断裂,则下列说法错误的是( )
A.小球的角速度突然增大
B.小球的瞬时速度突然增大
C.小球的向心加速度突然增大
D.小球对悬线的拉力突然增大
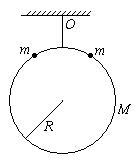 10.如图所示,有一质量为M的大圆环,半径为R,被一轻
10.如图所示,有一质量为M的大圆环,半径为R,被一轻
杆固定后悬挂在O点,有两个质量为m的小环(可视为
质点),同时从大环两侧的对称位置由静止滑下.两小环同时滑到大环底部时,速度都为
v,则此时大环对轻杆的拉力大小为( )
A.(2m+2M)g
B.Mg-2mv2/R
C.2m(g+v2/R)+Mg
D.2m(v2/R-g)+Mg
二、填空题(每题5分,共15分)
11.质量相等的两汽车以相同的速度v分别通过半径为R的凸形桥
顶P与凹形桥底P′时两桥面所受的压力之比为FP∶FP′
=________.
12.一网球运动员在离开网的距离12 m处沿水平方向发球,发球高度为2.25 m,网的高度为0.9 m。若网球在网上0.1 m处越过,则网球的初速度v0=___________m/s。(取g=10 m/s2,不计空气阻力)
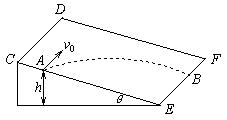
13.如图所示,将质量为m的小球从倾角为θ的光滑斜面上A点以速度v0水平抛出(即
v0∥CD),小球运动到B点,已知A点的高度h,则小球到达B点时的速度大小为______.
三、计算题(共35分)
14.(10分)射击运动员沿水平方向对准正前方100 m处的竖直靶板射击,第一发子弹射在靶上的A点,经测量计算,得知子弹飞行速度为500 m/s,第二发子弹击中A点正下方5 cm处的E点,求第二发子弹飞行速度。(不计空气影响,g=10 m/s2)
15.(12分)飞机在2 km的高空以100 m/s的速度水平匀速飞行,相隔1 s,先后从飞机上掉下A、B两物体,不计空气阻力,求两物体在空中的最大距离是多少?(g=10 m/s2)
16.(13分)如图所示,质量m=1 kg的小球用细线拴住,线长l=0.5 m,细线所受拉力达到F=18 N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5 m,重力加速度g=10 m/s2,求小球落地处到地面上P点的距离.(P点在悬点的正下方)
参考答案
1.B 2.B 3.D 4.A 5.D 6.BD 7.B 8.D
9.B解析:当细线碰到钉子时,线速度不变,但小球做圆周运动的半径将减小.
由ω=![]() ,R减小,ω增大 a=
,R减小,ω增大 a=![]() ,R减小,a增大
,R减小,a增大
F-mg=m![]() ,得F增大 故B错误,本题选B.
,得F增大 故B错误,本题选B.
10.C 解析:隔离一个小环,向上为正方向
FN-mg=m![]() FN=mg+m
FN=mg+m![]()
把大环和两个小环合起来作为研究对象
F=Mg+2FN=Mg+2m(g+![]() )
)
故C正确.
11.(gR-v2)∶(gR+v2)
12.24
13.解析:小球在光滑斜面上做类平抛运动,沿斜面向下的加速度a=gsinθ
由A运动至B的时间为t
沿斜面向下的位移为![]() =
=![]() at2
at2
所以t=![]() =
=![]()
小球到达B点的水平速度为vB.沿斜面向下的速度为
vy=at=gsinθ·![]() =
=![]()
故小球在B点的速度为
v=![]() =
=![]()
14.第一发子弹飞行时间t1=![]() s=0.2 s,则第一发子弹下落高度h1=
s=0.2 s,则第一发子弹下落高度h1=![]() gt12=0.2 m;第二发子弹下落高度h2=h1+0.05
m=0.25 m,下落时间t2=
gt12=0.2 m;第二发子弹下落高度h2=h1+0.05
m=0.25 m,下落时间t2=![]() s,则第二发子弹的初速度v2=
s,则第二发子弹的初速度v2=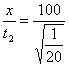 m/s=200
m/s=200![]() m/s.
m/s.
15.由于飞机水平匀速飞行,所以A、B两物体先后离开飞机后均做平抛运动,且水平速度都和飞机的水平速度相同,因此两物体在落地前始终在飞机的正下方,
它们的距离等于竖直位移之差.对A物体有:yA=![]() gt2
gt2
对B物体有:yB=![]() g(t-1)2
g(t-1)2
所以sAB=yA-yB=![]() gt2-
gt2-![]() g(t-1)2=
g(t-1)2=![]() g(2t-1)
g(2t-1)
随t的增大两物体距离增大,而物体A在空中飞行的最长时间为:
tm=![]() s=20 s
s=20 s
所以sAB大=![]() ×10×(2×20-1) m=195 m
×10×(2×20-1) m=195 m
16.球摆到悬点正下方时,线恰好被拉断,说明此时线的拉力F=18 N,则由
F-mg=m![]()
可求得线断时球的水平速度为
v=![]() m/s =2 m/s
m/s =2 m/s
线断后球做平抛运动,由h=![]() gt2
gt2
可求得物体做平抛运动的时间为t=![]() s=1 s
s=1 s
则平抛运动的水平位移为x=vt=2×1 m=2 m
