高二物理电磁学练习

一、选择题

1.如果一带电粒子在电场中只受电场力作用，那么它可能出现的运动状态是　(　　　 )

A.匀速直线运动.　　　　 B.匀变速直线运动.

C.匀变速曲线运动.　　　 D.匀速圆周运动.

答案：A、B、C、D

2.有一小段通电导线，长0.01m、电流5A，把它放入磁场中某一位置，受到的磁场力是0.1N，则该处磁感应强度的大小为　　(　　　 )

A.1T.　B.2T.　 C.大于2T.　D.小于2T.

答案：C

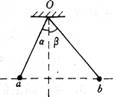3.用两根绝缘细线分别系住a、b两个带电小球，并悬挂在O点，当两个小球处于静止状态时，它们恰好在同一水平面上，此时α<β，如图所示.若将两细线同时剪断，在某一时刻(　　　 )

A.落在同一水平面上.

B.a球水平位移大于b的水平位移.

C.a球速度小于b球的速度.

D.a球速度大于b球的速度.

答案：A、C

4.如图所示，在a点放有一个带电量为－Q的点电荷，、在b焦放有一个带电量为+2Q的点电荷.在它们的连线上有M、N两点，且aM＝bN，比较M、N两点的电场强度大小和电势的高低，有(　　　　)

A.E_M>E_N.　 B.E_M<E_N.　 C.U_M>U_N.　 D.U_M<U_N.

答案：B、D

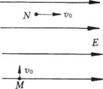5.如图所示，质量为m、电量为q的小球，以速度v₀，从M点垂直向上进入水平向右、电场强度为E的匀强电场中，到N点时速度变为水平向右的v₀.则小球从M点到N点过程中速度的最小值为(　　　 )

A..　　　B.　　 C.　　　　D.

答案：C

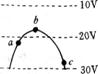6.图中三条平行等距的直虚线表示电场中的三个等势面，电势值分别为10V、20V、30V，实线表示一带负电的粒子在该区域内的运动轨迹，对于轨迹上的a、b、c三点来说 (　　　 )

A.粒子必先过a，再到b，然后到c

B.粒子在三点的受力F_a＝F_b＝F_c

C.粒子在三点的动能大小为E_b>E_a>E_c

D.粒子在三点的动能大小为E_c>E_a>E_b

答案：B、D

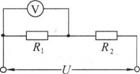7.如图所示，两个定值电阻R₁、R₂串联后接在输出电压U稳定于12V的直流电源上，再把一个内阻不是远大于R₁、R₂的电压表接在R₁的两端，电压表的示数为8V.如果再把该电压表改接在R₂的两端，则电压表的示数将　　　 (　　　 )

A.小于4V.　　　　　　　　　　　B.等于4V.

C.大于4V，小于8V.　　　　　　 D.等于或者大于8V.

答案：A[提示:电压表接R。时示数为8V，此时R₂上的电压为(12－8)V＝4V，即R₁和R_V并联电阻为R₂的2倍.现任意设定R₁＝3kΩ，R_V＝6kΩ(设定的这两个数据应便于计算)，则R₂＝1kΩ.再将电压表接R₂，同理可算得电压表示数为，选项A正确]

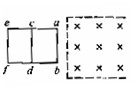8．如图所示，虚线框内是磁感应强度为B的匀强磁场，导线框的三条竖直边的电阻均为r，长均为L，两横边电阻不计，线框平面与磁场方向垂直。当导线框以恒定速度v水平向右运动，ab边进入磁场时，ab两端的电势差为U₁，当cd边进入磁场时，ab两端的电势差为U₂，则　　　　　　　　　　　 （　 ）

　　　A．U₁=BLv　　　　B．U₁=BLv　　　 

　C．U₂=BLv　　　　  D．U₂=BLv

答案：B.D

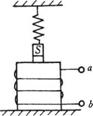9. .如图所示，弹簧秤下挂一条形磁棒，其中条形磁棒N极的一部分位于未通电的螺线管内，下列说法正确的是　(　 　　)

A.若将a接电源正极，b接电源负极，弹簧秤的示数将减小.

B.若将a接电源正极，b接电源负极，弹簧秤的示数将增大.

C.若将b接电源正极，a接电源负极，弹簧秤的示数将增大.

D.若将b接电源正极，a接电源负极，弹簧秤的示数将减小.

答案：A、C

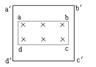10.如图所示，虚线框abcd内为一矩形匀强磁场区域，ab=2bc，磁场方向垂直于纸面；实线框a'b'c'd'是一正方形导线框，a'b'边与ab边平行。若将导线框匀速地拉离磁场区域，以W₁表示沿平行于ab的方向拉出过程中外力所做的功，W₂表示以同样的速率沿平行于bc的方向拉出过程中外力所做的功，则

A．W₁= W₂　　B．W₂=2W₁

C．W₁=2W₂　　D．W₂=4W₁

答案：B

二、实验题

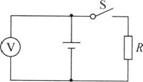
11.现有一阻值为10.0Ω的定值电阻、一个开关、若干根导线和一个电压表(该电压表表面上有刻度但无刻度值).要求设计一个能测定某电源内阻的实验方案(已知电压表内阻很大，电压表量程大于电源电动势，电源内阻约为几欧).要求:

 (1)在方框中画出实验电路图，并在图所示的实物图上完成接线图.

(2)简要写出完成接线后的实验步骤.

(3)写出用测得的量计算电源内阻的表达式r＝　　　　.

答案：(1)实验电路如图所示，实物图略(2)①断开开关，记下电压表偏转的格数N，；②合上开关，记下电压表偏转的格数N₂(3)r＝R＝(N₁－N₂)/N₂

12. 用欧姆表刻度盘中央刻线处标有"25”字样的多用电表测定两个定值电阻，其中R₁＝20Ω，R₂＝30kΩ，在下列的操作步骤中，合理的操作顺序应为　　　　.

A.将选择开关置于“×lkΩ"挡.

B.将选择开关置于“×100Ω"挡.

C.将选择开关置于“×10Q”挡.

D.将选择开关置于“×1Ω”挡.

E.将选择开关置于"OFF"挡.

F.将两表笔分别接触R₁两端，读出R₁的阻值后随即断开.

G.将两表笔分别接触R₂两端，读出R₂的阻值后随即断开.

H.将两表直接接触，调节“调零”旋钮，使指针指在刻度右端“0”刻度处后随即断开.

答案：D、H、F、A、H、G、E

三、计算题

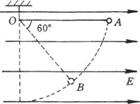13、如图所示，在水平方向的匀强电场中，用长为L的绝缘细线，拴住一质量为m、带电量为q的小球，线的上端固定.开始

时连线带球拉成水平，突然松开后，小球由静止开始向下摆动，当细线转动60°角时的速度恰好为零，问:

(1)A、B两点的电势差U_AB为多少?

(2)电场强度为多少?

答案：(1)(2)[提示:联解qU_AB＝mglsin60°和mglsin60°＝qEl(1－cos60°)即可]

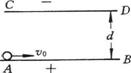14.如图所示，带等量异种电荷的两块相互平行的金属板AB、CD，长都为L，两板间距为d，其间为匀强电场.当两板间电压为U₀时，有一质量为m、带电量为q的质子紧靠AB板的上表面以初速度v₀射入电场中，设质子运动过程中不会和CD板相碰，求:

(1)当时，质子在竖直方向的位移是多大?

(2)当时，突然改变两金属板带电性质，且两板间电压为u₁，则质子恰好能紧贴B端飞出电场，求电压U₁和U₀的比值是多少?

答案：(1)[提示:质子进入电场的加速度为，当时，质子在竖直方向的位移为](2)3:1(提示:当时，质子在竖直方向的速度为，改变两极板的极性后，质子在竖直方向上的加速度为,y方向运动有:，可解得:U₁:U₂＝3:1)

15、图(a)为一个电灯两端的电压与通过它的电流的变化关系曲线.由图可知。两者不成线性关系，这是由于焦耳热使灯丝的温度发生了变化的缘故.参考这根曲线回答下；列问题(不计电流表和电池的内阻).

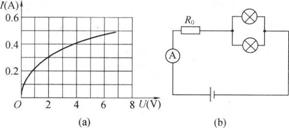(1)若把三个这样的电灯串联后，接到电动势为12V的电源上，求流过灯泡的电流和每个灯泡的电阻.

(2)如图(b)所示，将两个这样的灯并联后再与10Ω的定值电阻串联，接在电动势为8V的电源上，求通过电流表的电流值以及每个灯的电阻值.

解析　　(1)把三个这样的电灯串联后，每只电灯得到的实际电压为.再在图(a)上可以查到每只电灯加上4V的实际电压时的工作电流为I＝0.4A.由此可以求出在此时每只电灯的实际电阻.

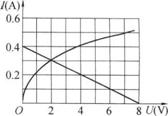 (2)在图(b)所示的混联电路中，设每只电灯上的实际电压和实际电流分别为U和I.在这个闭合电路中，电源电动势值应等于全电路电压降之和，即E＝U+2IR₀，代值并整理得U＝8－20I.这是一个反映电路约束(因电路结构特点而必须满足的电流、电压关系)的直线方程，把该直线在图(a)坐标系中画出，如图所示.而在该坐标系中原来就有一根反映元件约束(因元件即电灯的特点而必须满足的电流和电压关系)的曲线.这两条曲线的交点所表达的电流I和电压U，同时满足了电路结构和元件的要求，该元件实际上将工作在这个特定的电流和电压上，我们可以把这一点称作为该元件的“工作点”.现在我们可以在图上查出该工作点为U＝2V，I＝0.3A.这样，我们就可以求出此时每只灯泡的实际电阻.

16、 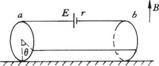如图所示，在绝缘的水平桌面上，固定着两个圆环，它们的半径相等，环面竖直，相互平行，间距为20cm.两环均由均匀的电阻丝制成，电阻都是9Ω，在两环的最高点a和b之间接有一个内阻为0.5Ω的电池，连接导线的电阻可忽略不计，空间有竖直向上的磁感应强度为3.46×10¹的匀强磁场，一根长度等于两环间距、质量为1.0×l0²kg、电阻为1.5Ω的均匀导体棒水平地置于两环内侧，不计与环间的摩擦，当将棒放在其两端点与两环最低点之间所夹圆弧对应的圆心角θ＝60°时，棒刚好静止不动，试求电源的电动势E.(g取l0m/s²)

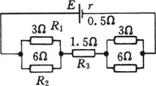解析　　导体棒将圆环分成长度之比为2:1的并联两部分，两部分电阻，，整个电路可整理成如图的直流电路.

由此司求出流过导体棒上的电流表达式

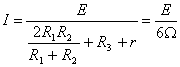　　　　　　　　　　　　　①

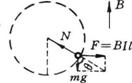再对导体棒受力分析如图所示，导体棒受力平衡，由∑F＝0，有

　　　　　　　　　　　　　　　　　　　　 ②

由安培力表达式，有F＝BIL.　　　　　　　　　　　　　③

联解①②③式，可解得.

代值计算得

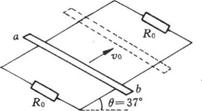17、如图所示，两根长度足够的平行导轨处在与水平方向成θ角的斜面上，θ＝37°，导轨电阻不计，间距L＝0.3m，在斜面上加有磁感应强度B＝1T、方向垂直于导轨平面的匀强磁场，导轨两端各接一个阻值R₀＝2Ω的电阻，一质量m＝1kg、电阻r＝2Ω的金属棒横跨在平行导轨间.棒与导轨间的滑动摩擦系数μ＝0.5，金属棒以平行于导轨向上的初速度v₀＝10m/s上滑，直至上升到最高点的过程中，通过上端电阻的电量Δq＝0.1C，求上端电阻R₀产生的焦耳热Q.

答案：作出等效电路图，设上滑s须历时t，平均电动势E＝BLs/t，总电流I＝E/R，支路电流I’＝I/2，通过上端电阻的电量Δq＝I’t＝BsL/2(R0/2+r)，解得s＝2m.

再由功能关系有mv₀²/2＝mgssin37°+mgscos37°+6Q，最后解得Q＝5J

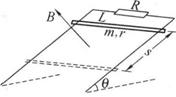18、如图所示，在倾角θ＝30°，相距L＝1m的光滑轨道上端连有一电阻R＝9Ω，整个轨道处于垂直轨道方向的磁感应强度B＝1T的匀强磁场中，现在轨道上由静止释放一质量m＝100g，电阻r＝lΩ的金属棒，当棒下滑s＝5m时恰好达到最大速度，不计导轨电阻.求:

(1)棒下滑的最大速度.

(2)电路在这个过程中产生的热量.

答案：(1)滑棒在下滑过程中速度最大时，加速度a为零，此时有:mgsinθ＝B²L²v_m/(R+r)，由此可解得最大速度v_m＝mgsinθ(R+r)/B²L²＝5m/s(2)由功能关系可求出滑棒在下滑过程中产生的热量Q＝mgssinθ－mv_m²/2＝1.25J.

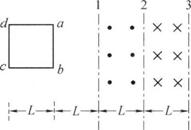
19、如图所示，在光滑的水平面上方，有两个磁感应强度大小相等、方向相反(都垂直于水平面)的磁场区域，它们的宽度均为L.现有一个质量为m、边长为L的正方形金属线框，在大小为F的水平恒力作用下，从静止开始运动，通过位移L进入磁场时恰好作匀速运动.试求:

(1)ab边刚进入磁场时，线框的速度v₁.

(2)当ab边刚越过磁场边界线2时，线框的加速度a.

(3)在ab边到达边界线3之前，线框已恢复作匀速运动，此时线框的速度v₂.

答案：(1)由动能定理FL＝2mv₁²/2，得.

(2)线框进入磁场1作匀速运动F_A＝B·BLv₁L/R＝F，在线框刚越过磁场边界线2时，速度还为v₁,ab、cd两条边同时切割磁感线，感应电动势加倍，两条边同时受磁场力作用，合力应为:4F－F＝3F，得此时线框加速度a＝3F/m，方向与拉力F的方向相反.

(3)当n6边到达磁场边界线3前，线框再次作匀速运动，F_A'＝4_B·BLv₂L/R＝F得