暑假专题——振动和波
教学过程:
![]()
2. 在一个周期内各物理量的变化规律见下表。
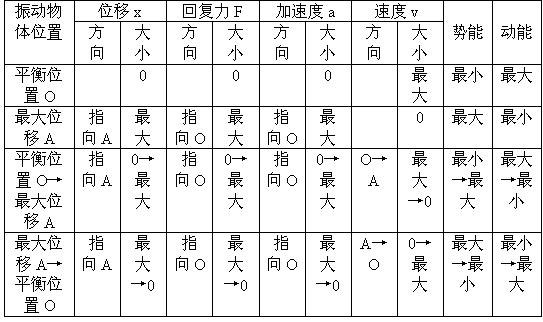
3. 简谐运动的图像
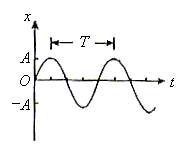
(1)坐标轴:横轴表示时间,纵轴表示位移。
(2)图线特点:正弦(或余弦)曲线。
(3)物理意义:表示做简谐振动的质点的位移随时间的变化规律。
4. 单摆周期公式中的l与g

(2)g为等效重力加速度
例如单摆置于以加速度a匀加速上升的升降机中,物体处于超重状态,加速度变为g'=g+a,此时回复力是视重mg'的切向分力,g'即为单摆的等效加速度。不论单摆处在什么情况下,在其平衡位置上的视重所“产生”的加速度,可等效为单摆的“重力”加速度。
5. 有关波的图像的几种常见问题:
(1)确定各质点的振动方向
如图所示(实线)为一沿x轴正方向传播的横波,试确定质点A、B、C、D的速度方向。
判断方法:将波形沿波的传播方向做微小移动,(如图中虚线)由于质点仅在y方向上振动,所以A'、B'、C'、D'即为质点运动后的位置,故该时刻A、B沿y轴正方向运动,C、D沿y轴负方向运动。
从以上分析也可看出,波形方向相同的“斜坡”上速度方向相同。
(2)确定波的传播方向
知道波的传播方向利用“微平移”的办法,可以很简单地判断出各质点的振动方向。反过来知道某一质点的运动方向,也可利用此法确定该波的传播方向。
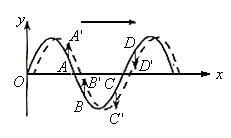
另外还有一简便实用的判断方法,同学们也可以记住。如图所示,若已知A点速度方向向上,可假想在最靠近它的波谷内有一小球。不难看出A向上运动时,小球将向右滚动,此即该波的传播方向。
(3)已知波速v和波形,画出再经△t时间的波形图
![]()
![]()
![]()
②特殊点法:(若知周期T则更简单)
在波形上找两个特殊点,如过平衡位置的点和与它相邻的波峰(谷)点,先确定这两点的振动方向,再看△t=nT+t,由于经nT波形不变,所以也采取去整nT留零t的方法,分别做出两特殊点经t后的位置,然后按正弦规律画出新波形。
(4)已知振幅A和周期T,求振动质点在△t时间内的路程和位移。
求振动质点在△t时间内的路程和位移,由于牵涉质点的初始状态,需用正弦函数较复![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. 波的干涉和衍射
【典型例题】
例1. 弹簧振子B的质量为M,弹簧的劲度系数为k,在B上面放一质量为m的木块A,使A和B一起在光滑水平面上做简谐运动,如图所示。振动过程中,A与B之间无相对运动,当它们离开平衡位置的位移为x时,A与B间的摩擦力大小为( )
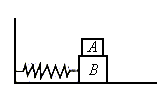
![]()
精析:木块A作简谐运动时,由题意和牛顿第二定律可得:
![]()
将木块A和振子B一起为研究对象,它们作简谐运动的回复力为弹簧的弹力所提供,应有
![]()
由<1>式和<2>式可得:
![]()
答案:C
说明:本题是讨论由静摩擦力提供A物体作简谐运动回复力的问题。这里特别要注意到当两物体达到最大位移时,振动时的加速度最大,A、B两个物体之间的静摩擦力是它们振动过程中的最大静摩擦力Fm',但不一定是A、B两物体之间的最大静摩擦力Fm,这两者之间的关系是Fm≥Fm'。
例2. 某弹簧振子的固有频率为2.5 Hz,将弹簧振子从平衡位置拉开4 cm后放开,同时开始计时,则有t=1.55s时( )
A. 振子正在做加速度减小的加速运动
B. 振子正在做加速度增大的减速运动
C. 振子的速度方向沿x轴正方向
D. 振子的位移一定大于2 cm
精析:![]()
根据简谐振动周期性的特点知:
![]()
振子在t=1.2s时的运动状态与t=0时相同,则t=1.55s时的状态与t=0.35s时的振动状态相同。作出振子的简谐运动图像如图所示,t=0.35s时,对应于图线上的P点,振子此时正在向最大正位移处运动,加速度正在增大,速度正在减小,速度方向为正方向,![]()
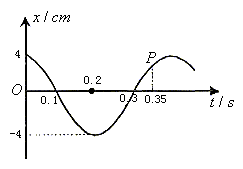
振动的往复性是振动的最大特点。每经过一个周期,质点的运动状态恢复。所以,没有必要将振子在1.55s内的简谐运动的图像都做出来,只要观察振子在一个周期内的运动情况,以后的运动情况可顺推出来。
例3. 水平轨道AB,在B点处与半径R=300m的光滑弧形轨道BC相切,一个质量为M=0.99kg的木块静止于B处。现有一颗质量为m=10g的子弹以v0=500m/s的水平速度从左边射入木块且未穿出,如图所示。已知木块与该水平轨道AB的动摩擦因数μ=0.5(cos5°=0.996,g取10m/s2)。试求:子弹射入木块后,木块需经多长时间停止?
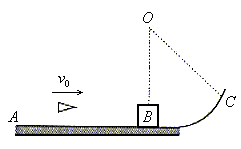
精析:该题所描述的物理过程可划分为三个阶段:第一阶段为子弹与木块发生碰撞获得共同速度;第二阶段为子弹与木块一起在光滑圆弧形轨道上运动;第三阶段为子弹与木块又从B点开始在水平面AB上做匀减速运动。
要求子弹射入木块后木块的运动时间,关键是第二个阶段所经历时间的计算,只有子弹与木块在BC面运动的幅度较小,才可将该阶段的运动看成等效单摆的运动,现估算如下:
![]()
![]()
由<1>式得:v=5m/s
![]()
与本题条件比较可知θ=5°,故子弹与木块在BC面上的一个往返时间为等效单摆![]()
![]()
![]()
故从子弹射入木块到它们停止共需经历18.2s。
说明:一切在竖直平面放置的光滑圆弧形内轨道上的小幅度运动(运动范围远小于圆弧半径,运动过程中所对应的圆心角小于5°),都可以等效为单摆模型,其等效摆长即![]()
例4. 如图所示为沿水平方向的介质中的部分质点,每相邻两质点间距离相等,其中O为波源。设波源的振动周期为T,自波源通过平衡位置竖直向下振动时开始计时,经过T/4,质点1开始起振,则下列关于各质点的振动和介质中的波的说法中错误的是( )
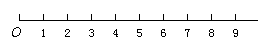
A. 介质中所有质点的起振方向都是竖直向下的,且图中质点9起振最晚
B. 图中所画出的质点起振时间都是相同的,起振的位置和起振的方向是不同的
C. 图中质点8的振动完全重复质点7的振动,只是质点8振动时,通过平衡位置或最大位移的时间总是比质点7通过相同位置时落后T/4
D. 只要图中所有质点都已振动了,质点1与质点9的振动步调就完全一致,但如果质点1发生的是第100次振动,则质点9发生的就是第98次振动
精析:由波的形成原理可知,介质中的质点总是重复波源的振动形式,起振方向相同,但振动开始的时间不同,后面的质点总是落后于前面的质点,故A正确,B错;从题中可知,质点7是质点8的前质点,7、8质点间的振动步调相差T/4,故C正确;质点9比质点1晚2T开始起振,一旦质点9起振后,1、9振动步调就完全一致,故D正确。
答案:B
例5. 如图所示,是一列横波在某一时刻的波形图,波沿x轴正向传播,则
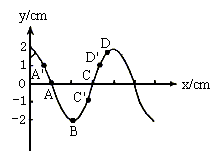
(1)A点的振动方向是_______________,C点的振动方向是_______________,D点的振动方向是_______________。
(2)再经T/2质点A通过的路程是__________cm,质点C的位移是__________cm。
精析:微平移法:(1)波沿x轴正向传播,波源在左方,则在A点的左方附近找一点A',见图。A'在A上方,故A向上运动。
同理在C左方附近找一点C',见图。C'在C下方,故C向下运动,同理知D向下运动。
(2)质点A在T/2时间内振动了1/2个全振动,通过路程s=2A=2×2cm=4cm,而要确定点C的位移,应先确定其运动方向,因C向下运动,经T/2,其刚好回到原来的地方,故其位移是0。
答案:向上,向下,向下,4,0
例6. 如图所示,在同一均匀媒质中有S1、S2两个波源,这两个波源的频率、振动方向均相同,且振动的步调完全一致,S1、S2之间相距两个波长,B点为S1、S2连线的中点,![]()
共有几个振动加强点?
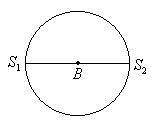
精析:首先让我们分析S1、S2两波源的连线上共有几个加强点
![]()
故A、C两点也为加强点,即S1、S2连线上共有三个加强点
再过A、B、C三点作三条加强线(表示三个加强区域),交圆周于A1、A2、B1、B2、C1、C2点,显然这6个点也为加强点,故圆周上共有6个加强点。
所以共有6个加强点。

【模拟试题】
1. 单摆作简谐运动的回复力是( )
A. 摆球的重力
B. 摆球所受的重力沿圆弧切线方向的分力
C. 摆球所受重力与悬线对摆球拉力的合力
D. 悬线对摆球的拉力
2. 如下图所示,一个小铁球,用长约10m的细线系牢,另一端固定在O点,小球在C处平衡。第一次把小球由C处向右侧移开约4 cm,从静止释放至回到C点所用时间为![]() ;第二次把小球提到O点,由静止释放,至到达C点所用的时间为
;第二次把小球提到O点,由静止释放,至到达C点所用的时间为![]() ,则( )
,则( )
A. ![]() B.
B.
![]()
C. ![]() D.
无法判断
D.
无法判断
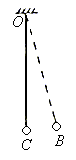
3. 一个单摆作简谐运动。若使摆球质量变为原来的4倍,而通过平衡位置时的速度变为原来的![]() ,则( )
,则( )
A. 频率不变,振幅不变
B. 频率不变,振幅改变
C. 频率改变,振幅不变
D. 频率改变,振幅改变
4. 一列简谐横波沿x轴正方向传播,波速![]() ,某时刻波形如图,则( )
,某时刻波形如图,则( )
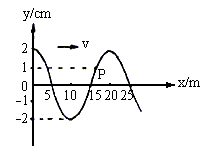
A. 这列波的波长为25 m
B. 质点P的振幅是1 cm
C. 质点P此时刻的速度方向沿y轴负方向
D. 质点P振动的周期为4s
5. 一个弹簧振子在AB间作简谐运动,O是平衡位置,以某时刻作为计时零点(t=0)。经过![]() 周期,振子具有正方向的最大加速度,那么以下几个振动图中哪一个正确地反映了振子的振动情况?( )
周期,振子具有正方向的最大加速度,那么以下几个振动图中哪一个正确地反映了振子的振动情况?( )
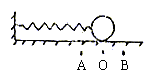
6. 图中两单摆摆长相同,平衡时两摆球刚好接触,现将摆球A在两摆线所在平面内向左拉开一小角度后释放,碰撞后,两摆球分开各自做简谐运动,以![]() 分别表示摆球A、B的质量,则( )
分别表示摆球A、B的质量,则( )
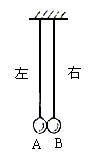
A. 如果![]() ,下一次碰撞将发生在平衡位置右侧
,下一次碰撞将发生在平衡位置右侧
B. 如果![]() ,下一次碰撞将发生在平衡位置左侧
,下一次碰撞将发生在平衡位置左侧
C. 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧
D. 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧
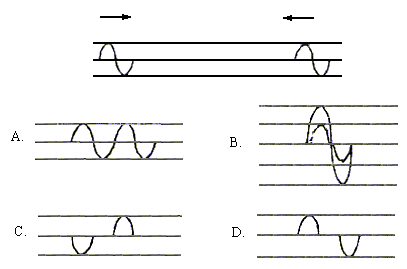
7. 从一条弦线的两端,各发生一如图所示的横脉冲,它们均沿弦线传播,速度相等,传播方向相反,在它们传播的过程中,可能出现的脉冲波形是下面图中的哪一个?
8. 在波的传播过程中,平衡位置相距半个波长的两个质点的振动情况是( )
A. 位移总相同 B. 速度的大小总相等
C. 加速度的大小总相等 D. 振幅总相同
9. 下图是甲、乙两个单摆作简谐运动的振动图线,可以断定甲、乙两个单摆的摆长之比![]() 等于( )
等于( )
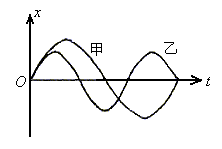
A. 9:4 B. 3:2 C. 4:9 D. 2:3
10. 图1所示为一列简谐横波在t=20秒时的波形图,图2是这列波中P点的振动图线,那么该波的传播速度和传播方向是( )
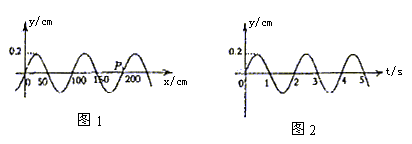
A. v=25cm/s,向左传播
B. v=50cm/s,向左传播
C. v=25cm/s,向右传播
D. v=50cm/s,向右传播
11. 图中实线表示横波甲和横波乙在t时刻的波形图线,经过1秒后,甲的波峰A移到A'点,乙的波峰B移到B'点,如两图中虚线所示。下列说法中正确的是( )
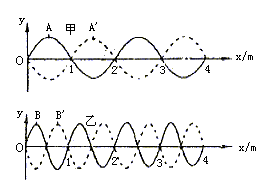
A. 波甲的波长大于波乙的波长
B. 波甲的速度小于波乙的速度
C. 波甲的周期等于波乙的周期
D. 波甲的频率小于波乙的频率
12. 公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动且不脱离底板,一段时间内货物在竖直方向的振动可视为简谐运动,周期为T。取竖直向上为正方向,以某时刻作为计时起点,即t=0,其振动图象如图所示,则( )
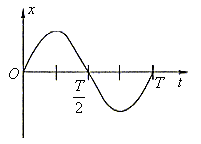
A. ![]() 时,货物对车厢底板的压力最大
时,货物对车厢底板的压力最大
B. ![]() 时,货物对车厢底板的压力最小
时,货物对车厢底板的压力最小
C. ![]() 时,货物对车厢底板的压力最大
时,货物对车厢底板的压力最大
D. ![]() 时,货物对车厢底板的压力最小
时,货物对车厢底板的压力最小
13. 关于多普勒效应的叙述,下列说法中正确的是( )
A. 产生多普勒效应的原因是波源频率发生了变化
B. 产生多普勒效应的原因是观察者和波源之间发生了相对运动
C. 甲乙两列车相向行驶,两车均鸣笛,且所发出的笛声频率相同,乙车中的某旅客听到的甲车笛声频率低于他所听到的乙车笛声频率
D. 哈勃太空望镜发现所接受到的来自于遥远星系上的某种原子光谱,与地球上同种原子的光谱相比较,光谱中各条谱线的波长均变长(称为哈勃红移),这说明该星系正在远离我们而去
14. 一个单摆从甲地拿到乙地,发现振动变快了。为了调整到原来的周期,以下说法正确的是( )
A. 这是因为![]() ,故应缩短摆长
,故应缩短摆长
B. 这是因为![]() ,故应加长摆长
,故应加长摆长
C. 这是因为![]() ,故应缩短摆长
,故应缩短摆长
D. 这是因为![]() ,故应加长摆长
,故应加长摆长
15. 均匀介质中,各质点的平衡位置在同一直线上,相邻质点的距离均为s,如图甲所示。振动从质点1由平衡位置开始向右传播,质点1从平衡位置开始运动时的速度方向竖直向上,经过时间t,前13个质点第一次形成如图乙所示的波形。关于这列波的周期和波速有如下说法( )
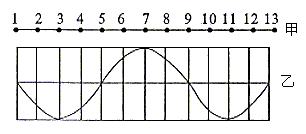
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
16. 两列平面简谐波在空中叠加,其中简谐横波a(图中虚线所示)沿x轴的正方向传播,简谐横波b(图中实线所示)沿x轴的负方向传播,波速都是20m/s,t=0时,这两列波的波动图象如图所示,那么位于x=45m处的质点P第一次达到波峰的时间和第一次处于平衡位置的时间分别是( )
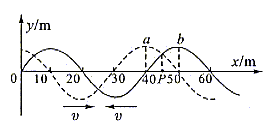
A. 1.50s 0.25s B. 0.25s 0.75s
C. 0.50s 0.75s D. 0.75s 0.25s
17. 在简谐纵波形成与传播过程中,t=0、t=T/4和t=T/2时刻的波动情况如图甲所示,设向右为正方向,若以t=T/4时刻的质点3振动的计时起点,则能够正确反映质点3振动位移随时间变化的图象是图乙中的( )
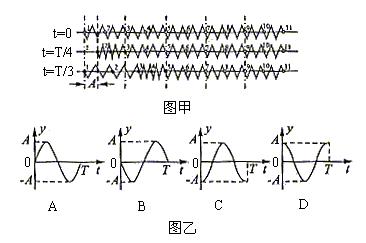
18. 如图所示为波源O振动1.5s时沿波传播方向上部分质点振动的波形图,已知波源O在t=0时开始沿x负方向振动,t=1.5s时它正好第二次到达波谷,问:
(1)何时y=5.4m的质点第一次到达波峰?
(2)从t=0开始至y=5.4m的质点第一次到达波峰这段时间内,波源通过的路程是多少?

【试题答案】
1. B 2. A 3. B 4. C
5. D 6. CD 7. ABD 8. BCD
9. A 10. B 11. D 12. C
13. BD 14. A 15. BD 16. B
17. A 18. 11.7s;1.95m