会考物理公式汇总及值得“look look”的历届考题

（注意并说明：本习题的计算中重力加速度取g=10m/s²）

（Ⅰ）力和运动（直线、曲线）、功和能的“综合”题

1、质量M＝6.0×10³kg的客机，从静止开始沿平直的跑道滑行，当滑行距离s＝7.2×10²m时，达到起飞速度v_t＝60m/s，求：

（1）起飞时飞机的动能是多大？

（2）若不计滑行过程中所受的阻力，则飞机受到的牵引力为多大？

（3）若滑行过程中受到的平均阻力大小为f＝3.0×10³N，牵引力与第（2）问中求得的值相等，则要达到上述起飞速度，所需的时间t为多大？飞机的滑行距离s^/应为多大？

2、一小球在某高处以v₀＝10m/s的初速度被水平抛出，落地时的速度v_t＝20m/s，不计空气阻力，求：

(1)小球被抛出处的高度H和落地时间t

（2）小球落地点与抛出点之间的距离s

(3)小球下落过程中，在何处重力势能与动能相等

3、如图所示，半径为R=0.45m的光滑的1/4圆弧轨道AB与粗糙平面BC相连，质量m＝1kg的物块由静止开始从A点滑下经B点进入动摩擦因数μ=0.2的平面。求：

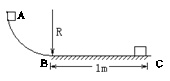（1）物块经B点时的速度大小v_t和距水平轨道高度为3R/4时速度大小v

（2）物块过B点后2s内所滑行的距离s

（3）物体沿水平面运动过程中克服摩擦力做多少功？

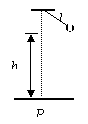4、如图所示，质量为m=1kg的小球用细线拴住，线长l=0.5m，细线受到F=18N的拉力时就会被拉断，当小球从图示位置释放后摆到悬点正下方时，细线恰好被拉断，若此时小球距水平地面高度h=5m，求：

（1）细线断时，小球的速度大小v₀

（2）小球落地点离地面上P点的距离x为多少？（P点在悬点正下方）

（3）小球落地时的速度大小v_t

（4）小球落地时重力的瞬时功率p

5、半径R=20cm的竖直放置的圆轨道与水平直轨道相连接，如图所示。质量为m=50g的小球A

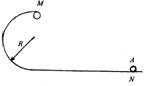以一定的初速度v₀由直轨道向左运动，并沿圆轨道的内壁冲上去，经过轨道最高点M时轨道对小球的压力为0.5N，然后水平飞出，落在水平轨道上。（不计一切阻力）求：

（1）小球经过M点时的速度v_M

（2）小球落地点与M点间的水平距离x

（3）小球经过N点时的速度v₀

1、解：（1）

（2）滑行过程中的加速度 a=v_t²/2s＝60²/（2×720）＝2.5m/s²　

牵引力F=ma=6000×2.5＝1.5×10⁴N

（3）此情况的滑行的加速度 a^/=（F－f）/m=（15000－3000）/6000＝ 2m/s²

所需时间 t=v_t/a^/=60/2＝30s　　滑行距离s^/=a^/t²/2=2×30²/2＝900m　

2、解：（1）由机械能守恒有 mv₀²/2 ＋ mgH＝mv_t²/2

则H＝

落地时间由H＝gt²/2得 t＝

（2）落地时水平距离 x＝v₀t ∴

（3）设h处重力势能与动能相等即E_K=E_P=mgh，则由 mv₀²/2 ＋ mgH=E_K＋E_P=2mgh

　　 得h＝v₀²/4g ＋ H/2＝10²/40 ＋ 15/2＝10m

3、解：（1）由机械能守恒得 mgR=mv_t²/2　　  v_t＝

由机械能守恒得 mgR＝mg3R/4＋mv²/2　 v＝

（2）物体做减速运动的加速度大小 a＝f/m＝μmg/m＝μg＝0.2×10＝2m/s²

∵物体停止时间　 ∴s＝

（3）克服阻力所做的功 ＝fs＝μmg s＝0.2×1×10×2.25＝4.5J

4、解：（1）由牛二定律得 F－mg＝　 ∴

（2）落地时间 　　∴　 x＝v₀t＝2m

（3）落地时  ∴（或由机械能守恒来求）

（4）P＝mgV_y＝1×10×10＝100W

5、解：（1）小球在M点时由牛顿第二定律 F_N+mg=mv_M²/R

　　　　 得v_M=

（2）小球离开M点作平抛运动 x=v_Mt＝v_M＝0.4

（3）从N→M由机械能守恒定律得 mv₀²/2＝mv_M²/2＋mg×2R

　　　　　 所以v₀＝

（Ⅱ）电磁感应中的电路问题、能量问题和运动问题

6、如图所示，一U形光滑金属框的可动边AC长L=0.1m，电阻为r=1Ω。匀强磁场的磁感强度为B=0.5 T，AC以v=8 m/s的速度水平向右移动，电阻R=7Ω，(其它电阻均不计)．求：

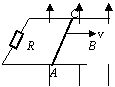（1）通过R的感应电流大小和方向；

（2）AC两端的电压；（3）使AC边匀速运动的外力大小；

（4）外力做功的功率

附注：《红皮书》第32页第33题务必要看（竖直框架的问题）！

7、如图所示，MN、PQ为光滑金属导轨（金属导轨电阻忽略不计），MN、PQ相距L=50cm，导体棒AB的电阻为r＝1Ω，且可以在MN、PQ上滑动，定值电阻R₁＝3Ω，R₂＝6Ω，整个装置放在磁感应强度为B=1.0T的匀强磁场中，磁场方向垂直与整个导轨平面，现用外力F拉着AB向右以v＝5.4m/s速度作匀速运动。求：

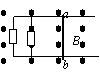 （1）导体棒AB产生的感应电动势E

和AB棒上的感应电流方向

（2）导体棒AB两端的电压U＝？

（3）外力F的大小及外力F做功的功率分别为多大？

（4）闭合电路中感应电流的电功率为多大？　　　　　　　　　　　　  　　（类似题图）

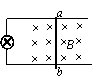8、如图所示，在足够长的平行金属轨道上放置一段长L=0.5m的金属棒ab，它的电阻r=1Ω。导轨的左端连接一只“2V，1W”的小灯泡，与导轨平面垂直的匀强电场的磁感应强度B=1T，方向如图所示。为使小灯泡正常发光，求：

 （1）小灯泡的电阻

（2）ab棒产生的感应电动势应多大？

（3）此金属棒向右运动的速度v

（Ⅲ）闭合电路欧姆定律和欧姆定律的“综合”题

9、如图所示电路中，电源电动势E=50V，内阻r=5Ω，电阻R₁=30Ω，R₂=60Ω。求：

  （1）流过电源的电流强度大小；

  （2）电压表示数为多少？

  （3）电阻R₂上的电功率

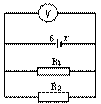
10、如图所示的电路中，电源电动势E = 6.0V ，内阻r = 0.6Ω ，电阻

R₂ = 0.5Ω ，当开关S断开时，电流表的示数为1.5A ，电压表的示

数为 3.0V ，试求：

（1）电阻R₁和R₃的阻值；

（2）当S闭合后，电压表的示数、以及R₂上消耗的电功率。

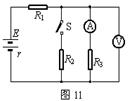
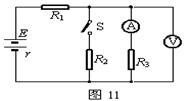11、如图所示的电路中，电阻R₁=14Ω，R₃=15Ω，电源的电动势E=12Ω，内电阻r=1Ω，电流表的读数I₃=0.2A，求：

（1）R₃电阻两端的电压U₃

(2）通过电源的电流I

（3）R₂的阻值

（4）电阻R₂消耗的功率P₂

6、解：（1）E=BLv＝0.5×0.1×8＝0.4v　I=E/（R＋r）＝0.4/（7＋1）＝0.05A　方向：斜向上

（2）U=IR=0.05×7＝0.35v　

（3）∵棒匀速，∴==BIL=0.5×0.05×0.1＝0.0025N （4）=v＝0.02W

7、解：（1）E=BLv＝1.0×0.5×5.4＝2.7v　　由右手定则知：棒上感应电流方向：A→B

（2）R₁R₂/（R₁＋R₂）=2Ω　 I=E/（＋r）＝2.7/（2＋1）＝0.9A　  U=I=0.9×2＝1.8v

（3）∵棒匀速　 ∴==BIL=1.0×0.9×0.5＝0.45N　=v＝2.43W

（4）=IE（或＝I²+I²r或＝）＝0.9×2.7＝2.43W

8、解：（1）=U²/P=2²/1＝4Ω　　　　　　 （3）v＝

（2）感应电流即电灯中的电流 I=P/U=1/2＝0.5A　∴棒产生的感应电动势 E=U＋Ir＝2＋0.5×1＝2.5V

9、解：（1）R₁R₂/（R₁＋R₂）=20Ω　 I=E/（＋r）＝50/（20＋5）＝2A

（2）电压表示数 U=I=2×20＝40v　（3）P₂=U²/R₂＝40²/60≈26.67W

10、解：（1）由题意知：开关断开时，R₁和R₃串联，I=I₃＝1.5A　　U₃=3.0V

　　　　　 而U₁＝E－Ir－U₃＝6.0－1.5×0.6－3.0＝2.1V

∴ R₁＝U₁/I＝2.1/1.5＝1.4Ω　　　 R₃＝U₃/I＝3.0/1.5＝2Ω

（2）当S闭合后，R₂和R₃并联，其并联阻值为 R₂R₃/（R₂＋R₃）=0.4Ω

此时电路中总电流I^/＝E/（＋r＋R₁）＝6.0/（0.4＋0.6＋1.4）＝2.5A

电压表的示数即并联部分两端的电压U^/＝I^/＝2.5×0.4＝1V　

R₂上消耗的电功率P₂＝U^/2/R₂＝1/0.5＝2W

11．解：（1）U₃＝I₃R₃＝0.2×15＝3v

（2）由闭合电路欧姆定律 E＝U＋Ir 得E＝IR₁＋U₃＋Ir

∴流过电源的电流I=A

（3）∵I=I₂＋I₃　∴I₂=I－I₃＝0.6－0.2＝0.4A　　又∵R₂与R₃　∴U₂＝U₃＝3v

　　　 　因此 R₂的阻值R₂＝U₂/I₂＝3/0.4＝7.5Ω

　　（4）R₂上消耗的电功率P₂＝U₂I₂＝3×0.4＝1.2W

（Ⅳ）公式汇总

1．滑动摩擦力：f＝μF_N　匀速运动：s＝vt 自由落体运动：　　  

2．匀变速直线运动：　　　  

推论：Δs=aT ²，即任意相邻相等时间内的位移之差相等

，某段时间的中间时刻的即时速度等于该段时间内的平均速度

初速为零的匀变速直线运动①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……

②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……

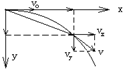
3．平抛运动：速度 ，合速度 　方向：tanθ=

位移x=v_ot　 y=　合位移大小：s=　方向：tanα=

落地时间由y=得t=（由下落的高度y决定）

4．匀速圆周运动：、、、的关系 v==w r=2rf

a=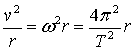　　　　　 

5．卫星圆周运动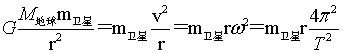：（式中r＝＋h）

1）由可得：　　r越大，v越小。

　　  又由v=wr和w =知：r越大，ω越小，T越大。

2）由可得： r越大，a_向越小。

6．恒力做功：W=Fscosθ 重力做功 W_G=mgh　 时间t内的平均功率 　 瞬时功率P=Fv

重力的瞬时功率可表示为P_G=mgv_y，即等于重力和物体在该时刻的竖直分速度之积。

汽车的问题：分析时采用的基本公式都是P=Fv和F－f = ma

7．机械能守恒定律的表达形式：，即；

8．单摆周期公式 （摆角θ<5⁰）

9．电磁波的波速、波长和周期的关系 c＝λ/T=λf　　 10．热力学第一定律 ΔU＝W+Q（吸热，Q取正值，放热，Q取负值；对外做功，W取负值，外界对物体做功，Q取正值）

11．电场强度 E＝F/q ，F＝Eq，元电荷的电荷量为1.6×10^-19C

12．电势差 U＝W/q，W_AB＝qU_AB＝q（φ_A－φ_B）（电势用符号φ来表示）

13．电容 C＝Q/U（定义式，但C与Q、U无关），C∝S/d（决定式即C由S、d决定的）

14．电流 I＝q/t，　　　　 电功率 P＝UI＝I²R＝U²/R　　　欧姆定律 I＝U/R

15．闭合电路欧姆定律 I＝E/（R＋r）、E＝U＋Ir＝IR＋Ir、R₁与R₂并联的阻值 R＝R₁R₂/（R₁＋R₂）

16．安培力F＝BIL（B⊥I），F＝0（B∥I）；洛仑兹力 F＝0（B∥V即磁场与电荷运动方向平行）

安培力、洛仑兹力方向判断：左手定则；磁通量 φ＝BS（单位：韦伯，符号Wb）

18．法拉第电磁感应定律 E＝nΔφ/Δt（用来计算回路中磁通量变化产生的感应电动势），

导体棒切割磁感线产生的感应电动势 E＝BLV（用来计算棒切割产生的感应电动势），由此产生的感应电流方向用：右手定则判断（切菜）　　　　氘核：、氚：

19．折射率 n＝sini/sinr＝c/v>1，全反射的临界角 sinC＝1/n

20．爱因斯坦在相对论中得出质量和能量关系：质能方程 E＝mc²或ΔE＝Δmc²；为解释光电效应，提出光子说。

21．有关光现象：（1）光的衍射：泊松亮斑、从单缝、单孔看到的彩色花纹

（2）光的直线传播：小孔成像、影的形成（日食、月食）、夏日树荫下的光斑

（3）光的全反射：海市蜃景、光导纤维、水珠在阳光下晶莹剔透、水或玻璃中的气泡特亮

（4）光的色散：雨后彩虹、白光经过棱镜出现彩色光带、透过玻璃边缘看到的彩色花纹

（5）光的干涉：马路上的油膜看到的彩色花纹、肥皂膜上看到的彩色花纹、双缝、双孔干涉

22．电磁波谱：无线电波→微波→红外线→可见光（红橙黄绿蓝靛紫）→紫外线→x射线→γ射线｛波长（频率）依次减小（增大）｝

23．放射性元素放出的（α、β、γ）射线（来自原子核）中：α射线电离作用最强，γ射线穿透作用最强

粒子	电子（带负电）	质子（带正电）	中子（不带电）	正电子	α粒子（氦原子核）
发现者或本质	注意：α、β射线不是电磁波	卢瑟福（人工核转变）	查德威克（人工核转变）	（发现正电子）
符号

24．常见的核反应方程及类型：①α衰变 、

②β衰变 、、

③人工核转变 　　　 ④重核裂变

⑤轻核聚变 、、、