08届高三物理统一测试试题
第Ⅰ卷（选择题 共40分）
一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确．全部选对的得4分，选不全的得2分，有选错或不答的得0分）
1．已知物体t时刻的末位置Q，要完全确定该物体在t=0时的初位置P，还必须知道
A．位移 B．路程 C．平均速率 D．平均功率
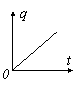2．一个阻值为R的电阻两端加上电压U后，通过电阻横截面的电量q随时间变化的图
象如图所示，此图象的斜率可表示为
A．U B．R
C．
D．
3．对下列规律理解正确的是
A．“
”只适用于匀速圆周运动 ，“
”只适用于匀速直线运动
B．“U=Ed” 只适用于匀强电场中的计算或推理，
说明UAB与q有关
C．“在各个连续相等的时间T内，△S=S2—S1=S3—S2=- - -=Sn—Sn-1= aT2”只适用于
初速度为零的匀加速直线运动
D．“第1个、第2个、第3个、- - -、第n个T时间内的位移S1：S2：S3：---：Sn =1：3：5：---：（2n—1）”只适用于初速度为零的匀加速直线运动
4．如图所示的非匀强电场中，如果电量q=10-5C的点电荷仅在电场力的作用下由A点
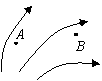移动到B点，电场力做功为8×10-3J，则
A．电场中A、B两点间的电势差800V
B．点电荷由A点移到B点电势能增加了8×10-3J
C．点电荷由A点移到B点电势能减少了8×10-3J
D．点电荷受到的电场力大小，在A点时比在B点时大
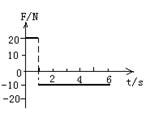5．如图所示表示作用在某物体上的合外力随时间变化的关系，若物体开始时是静止的，
则前3s内
A．物体的位移为0
B．物体的动量改变量为0
C．物体的动能改变量为0
D．物体的机械能改变量为0
6．如图所示，磁场方向竖直向下，通电直导线ab由图示位置1绕a点在竖直平面内转
到位置2，这个过程中通电直导线所受的安培力
A．数值变大，方向不变
B．数值变小，方向改变
C．数值不变，方向改变
D．数值、方向均改变
7．如图，绳子的一端固定在O点，另一端拴一重物在水平面上做匀速圆周运动
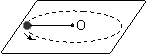A．转速相同时，绳长的容易断
B．周期相同时，绳短的容易断
C．线速度大小相等时，绳短的容易断
D．线速度大小相等时，绳长的容易断
8．如图所示，有一混合正离子束先后通过正交的电场、磁场区域Ⅰ和匀强磁场区域Ⅱ，如果这束正离子流在区域Ⅰ中不偏转，进入区域Ⅱ后偏转半径r相同，则它们一定具有相同的
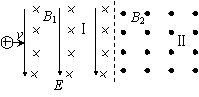A．速度
B．质量
C．电荷量
D．荷质比
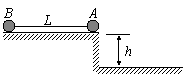
9．如图所示，质量均为m的小球A、B用长L的细线相连，放在高为h的光滑水平桌
面上（L＞2h）A球刚好在桌边并由静止开始滑落，若A、B两球落地后均不再弹起，则下列说法正确的是
A．A球落地前的加速度为
B．绳L对B球做的功为
C．A、B两球落地的水平距离为
D．B球离开桌面瞬间的速度为
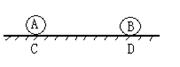
10．如图所示，完全相同的两个带电金属球A、B，初动能相同，在绝缘的光滑水平桌
面上沿同一直线从C、D开始相向运动，A球带电为+3q，B球带电为+2q；若两球是发生弹性碰撞，相碰后又各自返回C、D点，下列说法中正确的是
A．相碰分离后两球是同时返回C、D的
B．相碰分离后两球返回C、D时总动能增大
C．相碰前两球的总动量随两球的距离逐渐减小而增大
D．相碰前后的运动过程中，两球的总动量守恒、总动能守恒
第Ⅱ卷（非选择题 共110分）
二、实验题．本题共8小题，110分，解答应写出必要的文字说明、方程式和重要演算
步骤.只写出最后答案的不能得分.有数值计算的题，答案中必须明确写出数值和单位.
11．（12分）气垫导轨是常用的一种实验仪器，它是利用气泵使带孔的导轨与滑块之间
形成气垫，使滑块悬浮在导轨上，滑块在导轨上的运动可视为没有摩擦．我们可以用带竖直挡板C和D的气垫导轨和滑块A和B验证动量守恒定律，实验装置如图所示，采用的实验步骤如下：
a．松开手的同时，记录滑块A、B运动时间的计时
器开始工作，当A、B滑块分别碰撞C、D挡板时计时器结束计时，记下A、B分别到达C、D的运动时间t1和t2。
b．在A、B间水平放入一个轻弹簧，用手压住A、B使弹簧压缩，放置在气垫导轨上，并让它静止在某个位置。
c．给导轨送气，调整气垫导轨，使导轨处于水平。
d．用刻度尺测出A的左端至C板的距离L1；B的右端至D板的距离L2
(1) 实验步骤的顺序是
(2) 实验中还需要的测量仪器是
还需要测量的物理量是
（3）利用上述测量的实验数据，验证动量守恒定律的表达式是
（4）实验中弹簧与A、B滑块是粘连好还是不粘连好?
理由是
12．（12分）（1）若某多用电表Ω档的中央刻度值为“15”，用它测量阻值R约为1KΩ的电阻，应该把选择开关调至倍率为 档。
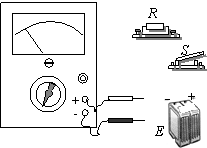（2） 若要测量该多用电表直流2.5 V档的内阻RV
(约为20kΩ)。
除此多用电表外，还有以下器材：直流电源一个（电动势E约为2V，内阻可忽略不计），电阻一个（阻值R约为10kΩ），电键一个，导线若干。
①写出实验步骤
②写出RV的表达式
13．（11分）用细线吊着一个小球，使小球在水平面内做半径为R匀速圆周运动；圆周运动的水平面距离悬点h，距离水平地面H。若细线突然在A处断裂，求小球在地面上的落点P与A的水平距离。
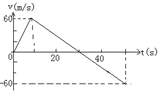14．（13分）一空间探测器的质量恒为3000kg，发动机推力为恒力。探测器从无大气层的某星球表面竖直升空，升空后发动机因故障而突然关闭；如图所示为探测器从升空到回落的速度—时间图象。求：
（1）探测器发动机的推力。
（2）若该星球与地球的半径之比为1：3，它们的质量比为多少？（地球表面处g=10 m/s2）
15．（15分）如图所示的真空中，场强为E的匀强电场，方向与竖直平面xOy平行且与
竖直轴Oy负方向成
=370的夹角。带电粒子以初速度v0=7.5m/s，从原点O沿着Ox轴运动，达到A点时速度为0，此刻，匀强电场的方向突然变为竖直向下，而大小不变，粒子又运动了t2=2s。（g=10 m/s2）求：
（1）粒子的带何种电荷、粒子到A点前作什么运动
（2）带电粒子运动t2后所在位置的坐标
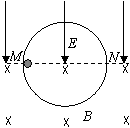16．（15分）如图所示，有位于竖直平面上的半径为R的圆形光滑绝缘轨道，其上半部分处于竖直向下、场强为E的匀强电场中，下半部分处于水平向里的匀强磁场中；质量为m，带正电为q的小球，从轨道的水平直径的M端由静止释放，若小球在某一次通过最低点时对轨道的压力为零，求：
（1）磁感强度B的大小。
（2）小球对轨道最低点的最大压力。
（3）若要小球在圆形轨道内作完整的圆周运动，小球从轨道的水平直径的M端下滑的最小速度。
17．（16分）如图所示，在光滑水平面上有物块A、B，可看作质点的物块C放在B的
右端，开始时用手使A、B之间压缩了一根劲度系数较大的轻弹簧，弹簧与物块A、B都不粘连；然后突然放手使A、B各自向左、右弹射出去，在B向右运动过程中，C最终停在B上。已知弹簧被手压缩时的弹性势能E=12J，三物块的质量为
，C与B之间的动摩擦因数
=0.2，求：(1)B的长度L至少多长。（2）若C是在突然放手的同时，以v0=3 m/s向左运动，求C相对地面向左运动的最大位移S。（设B足够长的）
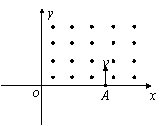
18.（16分）如图所示，在xoy区域内的第Ⅰ象限内有磁感应强度为B的匀强磁场，方向垂直xoy平面向外，区域内的其他象限无磁场。在A（L，0）点有一电子以速度v沿y轴正方向射入磁场。求电子在磁场中的运动时间。
参考答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | C | D | ACD | BC | A | AC | AD | ABC | AB |
11．解答：（每小问3分，共12分）
(1)c、b、d、a； (2)天平，滑块A、B的质量mA、mB；；
（3）
（4）（答案是开放的，只要合理就给3分，参考答案有：只与A、B中的某一个粘连好，这样把弹簧的质量考虑进去，会减小系统误差。不粘连好，否则A、B可能碰不到C、D，使计时误差大。等等）
12．解答：（1）应该把选择开关调至倍率为“×100”档。（2分）
（2）①第一步：选用多用电表的Ω档，进行电阻调零，然后测出电阻的阻值R；（2分）
第二步：用多用电表直流电压2.5 V档直接接在直流电源的两端测出电源的电动势E； （2分）
第三步：将多用电表选择在直流电压的2.5 V档，且将其与电阻R、电键串联后接在直流电源的两端；闭合电键，记下多用电表的电压读数U；断开电键，再根据欧姆定律列式计算RV。（3分）
②RV
=
（由电路中的电流
推得）（3分）
（注：第一步与第二步的秩序可以对调，只要能表达完整的意思即可）
13．解： 设小球在水平面内做半径为R匀速圆周运动的速度为v
根据
有 
（3分）
则
（2分）
若细线突然在A处断裂，小球以v作平抛运动，在地面上落点P的位置是在与A处的切线在同一竖直平面上，设离A处的水平距离为S
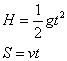（4分）
解得
（2分）
14．解：（1）由速度—时间图象知，0—10s在发动机的推力作用下探测器作匀加速直线运动，10s后探测器只受重力而作匀减速直线运动。设该星球表面附近的重力加速度为g星，探测器发动机的推力为F。
在10s后：
（2分）
则g星=3m/s2 （1分）
在0—10s内：
（2分）
据牛顿第二定律有
（2分）
得
（1分）
（2）在天体表面附近的物体，有
则
（3分）
（2分）
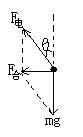15．解：（１）由于带电粒子沿着Ox轴运动，根据受力分析知：粒子一定带负电；（2分）
粒子前阶段是沿着Ox轴作匀减速运动。（2分）
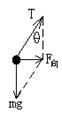
（2）前阶段，根据受力分析图知：
-----2分
a1
=
=7.5m/s2
―――（１）（2分）
又据
―――（2）（1分）
x=s=3.75m
（1分）
（或用动能定理求解）
电场的方向改变后，粒子是沿着垂直Ox轴作竖直向上的匀加速运动。
a2
=
=
=2.5m/s2 ―――（3）（2分）
=5m
―――（4）（2分）
带电粒子的位置坐标为（3.75m，5m） （1分）
16．解：（1）小球在轨道上来回运动时受重力、支持力、洛伦兹力，但只有重力做功，因此小球的机械能守恒。
从M到最低点有 
-----------（1）（2分）
在最低点有 
即
-----------（2）（2分）
联解（1）（2）得
（1分）
（2）小球从M到N以及在轨道上来回运动时受重力、支持力、洛伦兹力，但总只有重力做功，因此小球的机械能始终守恒。从N到最低点时对轨道最低点的有最大压力。（1分）
在最低点有
-----------（3）（2分）
联解（1）（3）得N2=6mg （1分）
（3）要小球在圆形轨道内作完整的圆周运动，此时对圆形轨道的最高点压力为零，（1分）
设小球从轨道的水平直径的M端下滑的最小速度为v0，在最高点速度为v1。
从M→轨道的最高点，据动能定理：
-----------（4）（2分）
在圆形轨道的最高点：
-----------（5）（2分）
联解（4）（5）得
（1分）
17．解：（１）由于弹簧与物块A、B不粘连，突然把压缩的轻弹簧放手，使A、B在短时间弹射出去，此时C的速度不改变，仍然为0。设B、C质量均为
，放手后A 、B的速度分别为v1、、v2
A、B系统的动量守恒 0= m A v1- m v2 ―――（１）（2分）
A、B和弹簧组成的系统的机械能守恒 E=
―――（2）（2分）
代入数据解得 v2=4m/s （1分）
设B、C同速为v3，B、C系统的动量守恒 m v2 = 2m v3 ―――（3）（2分）
得 v3= 2m/s （1分）
对B、C系统，椐能量转化与守恒定律，摩擦生热Q=ΔEK
f S相=
―――（4）（2分）
即mgL=
代入数据解得B的最短长度L =2m （2分）
（2）因为B、C都作加速度大小相同的匀减速运动，C先将速度减到零，以后再向右运动，则C将速度减到零时有向左运动的最大对地位移S。
对C，据动能定理 W=ΔEK
—mg S=0—
―――（5）（2分）
代入数据解得S= 2.25m （2分）
18．解：设电子以v0的速度射入磁场时，刚好从原点O离开磁场（如图），这时电子在磁场中的运动半径为：
--------2分
又
---------2分
得：
-------1分
（1）当电子速度
时，其运动半径小于或等于
，电子将从x轴上的某点离开磁场，运动时间为半个周期，（2分）
--------2分
（2）当电子速度
时，其运动半径大于，电子将从y轴上某点（如D点）离开磁场。（1分）
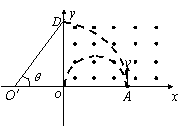设此时的圆心为O′，由图可知，
-------3分
所以：
----3分