高三物理上册期末迎考复习试卷（四）

考试时间：100分钟　　 满分：120分　　　

一、选择题（本题共8小题，每小题４分，共32分。在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。全选对的得4分，选不全的得2分，有选错或不答的得0分。）

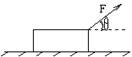1. 物体静止在水平面上，今对物体施加一个与水平方向成θ角的斜向上的拉力F，保持θ角不变，使F从零开始逐渐增大的过程中，物体始终未离开水平面，在此过程中物体受到的摩擦力将:　　

A. 逐渐增大　　　　　　　　  　B. 逐渐减小　　

C. 先逐渐增大后逐渐减小　　　　D. 先逐渐减小后逐渐增大

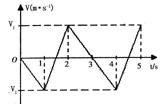2. 某物体受到合力F的作用，由静止开始运动，其v-t图象如图所示，由图可知

A．该物体只向一个方向运动

B．该物体所受的合力F方向不断变化，而大小始终不变

C．3 s末物体回到原出发点

D．2 s～4 s内，合力F做的功等于零

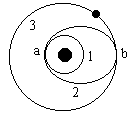3、如图所示，是某次发射人造卫星的示意图。人造卫星先在近地的圆周轨道1上运动，然后改在椭圆轨道2上运动，最后在圆周轨道3上运动。a点是轨道1、2的交点，b点是轨道2、3的交点．人造卫星在轨道1上的速度为v₁，在轨道2上a点的速度为v_2a，在轨道2上b点的速度为v_2b，在轨道3上的速度为v₃，则以上各速度的大小关系是

A．v₁＞v_2a＞v_2b＞v₃　　B．v₁ < v_2a < v_2b < v₃

C．v_{2 a}＞v₁＞v₃ ＞v_2b　　　D．v_{2 a}＞v₁＞v_2b＞v

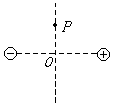
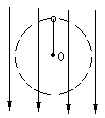
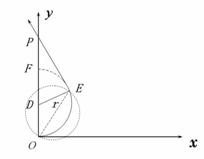
4. 如图所示，O为两个等量异号点电荷连线中点，P为连线中垂线上的任意一点，分别用U₀、U_P、E₀、E_P表示O、P两点的电势和场强的大小，则

A. U₀＞U_P，E₀＞E_P　 B. U₀=U_P，E₀＞E_P

C. U₀＜U_P，E₀＞E_P　 D. U₀＞U_P，E₀=E_P

5.如图所示，在方向向下的匀强电场中，一个带负电的小球被绝缘细线拴住在竖直面内做圆周运动，则

A.小球可能做匀速圆周运动

B.当小球运动到最高点时，线拉力一定最小

C.当小球运动到最高点时，电势能最大

D.小球在运动过程中，机械能一定不守恒

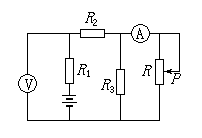6.如图所示电路中，电源的电动势为ε，内电阻为r，当变阻器R的滑片P向上移动时，电压表V的示数U和电流表A的示数I变化的情况是：

A. U变大，I变大；　　B. U变小，I变小；

C. U变大，I变小；　　D. U变小，I变大。

7.一个质量为m、带电量为q的粒子从两带电平行板的正中间沿与匀强电场垂直的方向射入，如图所示，不计粒子所受的重力，当粒子的入射速度为时，它恰能穿过这一电场区域而不碰到金属板上．现欲使质量为m、入射速度为的粒子从两带电平行板的正中间沿与匀强电场垂直的方向射入，也能恰好穿过这一电场区域而不碰到金属板，在以下的仅改变某一物理量的方案中，可行的是：

　　A．使粒子的带电量减少为原来的1／4；

　　B．使两板间所接电源的电压减小到原来的一半；

　　C．使两板间的距离增加到原来的2倍；

　　D．使两极板的长度减小为原来的一半．

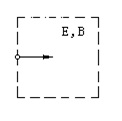8.在图中虚线所围的区域内，存在电场强度为E的匀强电场和磁感应强度为B的匀强磁场，已知从左方水平射入的电子，穿过这个区域时未发生偏转，设重力可以忽略不计，则在这区域中的E和B的方向可能是

A. E和B都沿水平方向，并与电子运动的方向相同

B. E和B都沿水平方向，并与电子运动的方向相反

C. E竖直向上，B垂直纸面向外

D. E竖直向上，B垂直纸面向里

二、本题共有7小题，按题目要求作答。计算题应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分，有数值计算的题，答案中必须写出数值和单位。

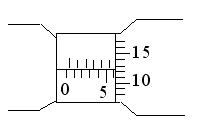
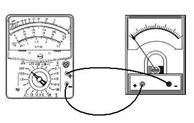
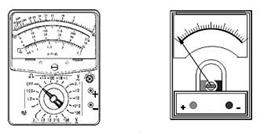
9.（10分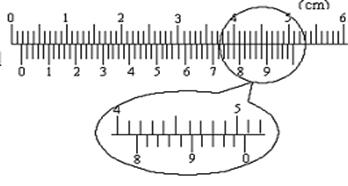）⑴读出下面两图的读数:左图 　　　　cm，右图　　　　mm。

　 

⑵下面是一位教师的《探究外力（重力）对物体所做的功与物体动能的变化关系实验》的教案，认真阅读下列材料，并回答问题：

【探究实验】外力（重力）对物体所做的功与物体动能的变化关系

㈠提供的实验器材有：电火花式打点计时器、纸带、重锤、刻度尺。

㈡请同学们根据已有的知识，结合提供的实验器材，在小组讨论的基础上，写出你们的实验方案。讨论时请围绕下列问题进行：

①如何设计实验方案。（实验结束后叫学生上台演示其实验操作过程）

【师生探讨】：将打点计时器侧放于桌面上，使限位孔伸出桌面外，将夹有重锤的纸带从下向上穿过限位孔，用一手压住打点计时器，另一手提住纸带的上端，使纸带竖直，重锤紧靠在下边的限位孔处，先开启电源使打点计时器工作，然后放手使纸带在重锤的带动下自由下落，结果打点计时器在纸带上打下一系列点，利用打了点的纸带来计算重力所做的功与动能变化量的定量关系。

②如何计算重力所做的功和动能的变化量。

【师生探讨】：在纸带上取两个合适的点（如下图中纸带上的B点和E点），用刻度尺测出这两点间的距离，根据功的定义可知：，采用求平均速度的方法求出打点计时器打B、E两点时，重锤的速度v_B和v_E， 再根据动能的计算式计算打B、E两点时的动能及其动能的差值。

③需要测量和记录哪些实验数据：（实验后由学生用图示方式板书出来）

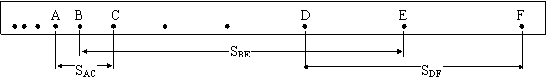④如何设计记录数据的表格：（学生板书并填入实验记录的数据）

SBE	SAC	SDF	tAC	tDF

㈢操作实验，测量和记录实验数据。

㈣数据处理表格：（学生板书并填入数据处理结果）

㈤处理实验数据，比较得出实验结论：

【生】：通过数据处理可知：重力所做的功与物体动能的改变量在误差允许的范围内是相等的。

　　请你在“㈣数据处理表格：”中，补写出和的表达式。

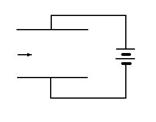
10. （10分）为了测量一个欧姆表内部电源的电动势，某同学仅利用提供给他的一个量程满足要求，内阻约2千欧的电压表完成了测量．已知欧姆表刻度盘上中央刻度值为‘20’．

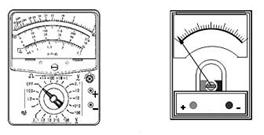　①请在图中用实线把两表连接成测量电路．

  ②实验中应把欧姆表选择开关调至　　　 挡．

  ③若实验中电压表示数为U，欧姆表指针所指的刻度为N，设一切操作均正确，则欧姆表电源电动势E的计算式为　　  ．

11. （12分）在沿直线运行的火车车厢内的后壁，张贴的列车时刻表在火车刹车时恰好脱落. 请你运用所学的物理知识计算， 列车时刻表落地点与车厢后壁的距离. 火车刹车时的速度为V， 火车刹车时加速度的大小为a， 时刻表脱落时底部距地板的高度为H，下落过程为平动.

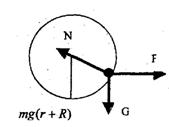
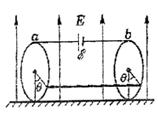12. （12分）如图所示，在绝缘的水平桌面上，固定着两个圆环，它们的半径相等，环面竖直、相互平行，间距是20cm，两环由均匀的电阻丝制成，电阻都是9，在两环的最高点a和b之间接有一个内阻为0.5的直流电源，连接导线的电阻可忽略不计，空间有竖直向上的磁感强度为3.46×10^-1T的匀强磁场.　一根长度等于两环间距，质量为10g，电阻为1.5的均匀导体棒水平地置于两环内侧，不计与环间的磨擦，当将棒放在其两端点与两环最低点之间所夹圆弧对应的圆心角均为时，棒刚好静止不动，试求电源的电动势（取

13．（14分）一行星探测器，完成探测任务后从行星表面竖直升空离开该行星。假设该探测器质量恒为M=1500kg，发动机工作时产生的推力为恒力，行星表面大气层对探测器的阻力大小不变。　探测器升空后一段时间因故障熄灭，发动机停止工作。图示是探测器速度随时间变化的关系图线。已知此行星的半径为6000km，引力常量为G=6.67×10^-11N·m²／kg² ，并认为探测器上升的高度范围内的重力加速度不变。求：

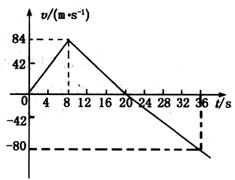　(1)该行星表面的重力加速度；

　(2)探测器发动机工作时产生的推力；

　(3)该行星的平均密度。

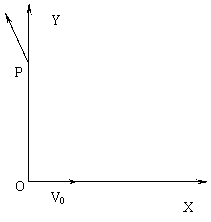14. (15分)一个质量为m，带电量为q的带电粒子（不计重力），以初速v₀沿X轴正方向运动，从图中原点O处开始进入一个边界为圆形的匀强磁场中，已知磁场方向垂直于纸面，磁感强度大小为B.粒子飞出磁场区域后，从P处穿过Y轴，速度方向与Y轴正方向的夹角为θ=30⁰， 如图所示，求：

（1）圆形磁场的最小面积。

（2）粒子从原点O处开始进入磁场到达P点经历的时间。

15. （15分）如图光滑斜面的倾角α＝30°，在斜面上放置一矩形线框abcd，ab边的边长L₁＝1m，bc边的边L₂＝0.6m，线框的质量m＝1kg，电阻R＝0.1Ω，线框通过细线与重物相连，重物质量M＝2kg，斜面上ef线（ef∥gh∥ab）的右方有垂直斜面向上的匀强磁场，磁感应强度Ｂ＝0.5T，如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef线和gh线的距离s＝11.4m，（取g＝10m/s²），求：

⑴线框进入磁场时匀速运动的速度v；

⑵ab边由静止开始运动到gh线所用的时间t；

⑶t时间内产生的焦耳热．　

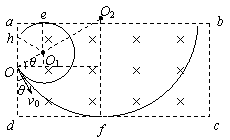
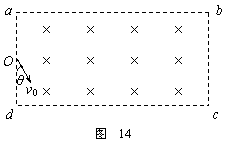16．（15分）如图14所示，一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场，在ad边中点O，方向垂直磁场向里射入一速度方向跟ad边夹角θ = 30°、大小为v₀的带正电粒子，已知粒子质量为m，电量为q，ad边长为L，ab边足够长，粒子重力不计，求：

（1）粒子能从ab边上射出磁场的v₀大小范围。

（2）如果带电粒子不受上述v₀大小范围的限制，求粒子在磁场中运动的最长时间。

答案

一、选择题　　1.C　2.CD　3.C 4.B　 5.AD 6.C　7.ACD　8.ABC　

二、9.（10分）⑴左图  0.194 cm，右图 6.124～6.126 mm。

⑵数据处理表格：（学生板书并填入数据处理结果）

10.　⑴

⑵ ×100　　　 ⑶

11. 解：列车时刻表落地时间：　　 ································· 3分

时刻表的位移　　  ·································  3分　　　　

（1）如果列车时刻表落地时，火车已经停下来：　　火车的位移····················2分

　　　　-　　 　································· 2分

　 （2）如果列车时刻表落地时，火车还没有停下来：火车的位移··············2分

　 　　　　　 　·································2分

12. 解：导体棒的受力分析如图所示，则依牛顿第二定律

　 有：　　　　　········４分

　　　　　　　········１分

　 所以：　　　　　　········１分

　　　　·········2分

由电路可以求得，·········4分　　　 代入数值可得：E=15V　　·········2分

13.(1) 根据图象和运动学公式可知：0～8s内，探测器的加速度a₁=10.5m/s²　·······１分

　　　　　　　　　  　　　　　　 8～20s内，探测器的加速度a₂=7 m/s²　　······１分

20～36s内，探测器的加速度a₃=5m/s²　　······１分　

设空气阻力为f，根据牛顿第二定律，

8～20s内：　 ｍｇ＋ｆ＝ｍａ_２　　　　  ···································1分

20～36s内：　ｍｇ－ｆ＝ｍａ_３　　　　　 ··································1分

∴　ｇ＝６m/s²　　　　 　　　　·································1分

　 　　　　　　f ＝1500 N　　　　　　　 ··································1分

(２)　 根据牛顿第二定律，

0～8s内：　　Ｆ－ｍｇ－ｆ＝ｍａ_１　　　 ··································2分

∴　Ｆ＝26250 N　　　　　　  ··································1分

(3)　　在行星表面根据　  ··································2分

　　　　　　　　　　　　　 ··································1分

　　　　　　　　　得：　kg/m³ ·······················2分

14.解：（1）根据 　得：粒子的轨道半径　  ·······4分

当圆形磁场以OE为直径则其面积最小。

　　 

∴ 圆形磁场的最小面积：　  ······4分

（2）　　　　　 ·······························2分

粒子从原点O处开始到离开磁场，轨道对应的圆心角为120⁰

∴在磁场中的运动时间为　 ································1分

由E到P点为匀速直线运动：　　　　　　　  ······························2分

∴粒子从E到P点经历的时间为 ·································1分

粒子从原点O处开始进入磁场到达P点经历的时间为：　  ·········1分

15. 解：⑴因为线框进入磁场的最初一段时间做匀速运动，所以重物受力平衡　　 

线框abcd受力平衡 　　 ·································1分

ab边进入磁场切割磁感线，产生的电动势　　　　····················1分

形成的感应电流　　　　　　 ·································1分

受到的安培力　　　　　　　　　 ·································1分

联立得：　　　　  ·································1分

解得　　　　　　　　　　　  　·································1分

⑵线框abcd进磁场前时，做匀加速直线运动；进磁场的过程中，做匀速直线运动；进入磁场后到运动到gh线，仍做匀加速直线运动。

进磁场前　 对M :　　　　　　　　　　　　　　　　　　　　　　　　　 ·································1分　　

　　　　  对m :  　　  ·································1分

联立解得：　　 ·································1分　　

该阶段运动时间为　　　　 ·································1分

进磁场过程中　 匀速运动时间　　　　····················1分　

进磁场后　 线框受力情况同进磁场前，所以该阶段的加速度仍为

　　　　　　　　　　  ·································1分

 　　  解得：　　························1分

因此ab边由静止开始运动到gh线所用的时间：····1分

⑶ J　　　　·································2分

16．（1）＜v₀≤（2）

解析：（1）若粒子速度为v₀，则qv₀B =，

　　所以有R =，

　　设圆心在O₁处对应圆弧与ab边相切，相应速度为v₀₁，则R₁＋R₁sinθ =，

　　将R₁ =代入上式可得，v₀₁ =

　　类似地，设圆心在O₂处对应圆弧与cd边相切，相应速度为v₀₂，则R₂－R₂sinθ =，

　　将R₂ =代入上式可得，v₀₂ =

　　所以粒子能从ab边上射出磁场的v₀应满足＜v₀≤

（2）由t =及T =可知，粒子在磁场中经过的弧所对的圆心角α越长，在磁场中运动的时间也越长。由图可知，在磁场中运动的半径r≤R₁时，运动时间最长，弧所对圆心角为（2π－2θ），

　　所以最长时间为t ==

答题纸

班级　　　　　　 姓名　　　　　

一、选择题

1	2	3	4	5	6	7	8

二、9.（10分）⑴左图 　　　　　　　 cm，右图　　　　　  mm。

⑵数据处理表格：（学生板书并填入数据处理结果）

SBE		SAC		SDF		tAC		tDF

10.　⑴

⑵ 　　　 　　　

⑶ 　　　　　 

三、计算题。本题共6小题，64分。按题目要求作答。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题答案中必须明确写出数值和单位。

11解：

12解：

13解：

14解：

15解：

16解：