高三物理第三次月考题

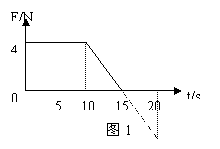15、在光滑水平面上做直线运动的物体，

其初速度为2m/s，质量m=2kg。t=0时，初

速度与水平恒力方向相同，所受水平恒力与

时间关系如图1所示。在0-20s内，力F对

物体所做的功为

A.484J　　　　 B.480J　　　  C.488J　　　 D.500J

16、高速轿车中常使用一种安全气袋，以防止撞车时坐在车内的人因向前冲撞发生意外，这种气袋装有一种能在高压下分解出气体的混合粉末。撞车时，约在1×10^-2S内袋内充满N₂而胀大，阻止人体前冲。在以后的0.1~0.2S内气体又“消失”。若轿车以126km/h的速度行驶时发生撞车。由于气袋的作用撞车后质量为60kg的人在0.35S内速度减为零，则气袋在撞车时对人的平均作用为

A.5000N　　　　 B.5400N　　　  C.6000N　　  D.6600N

17、关于布朗运动，以下认识正确的是

A.　 布朗运动就是液体分子的无规则运动

B.　 悬浮微粒越大，布朗运动越显著

C.　 液体温度越高，布朗运动越显著

D.　　 布朗运动是液体分子对固体分子的作用不平衡而形成的固体分子的无规则运动

18、宇宙飞船的速度v=7.5×10³m/s，它的横截面积s=4m²，在飞行中飞船与流星云中的微尘发生碰撞，假设每立方米的空间内有一个流星云微尘，每粒微尘的质量m=2.0×10kg，为使飞船的速度不发生变化，飞船发动机的牵引力应增加多少牛顿？

A.4.5×10N　　B. 4.5×10N　　C. 5×10N 　D. 5×10N

19、在光滑水平的上有A、B两小球沿同一直线向右运动，A追上B并发生对心正碰，设向右为正方向。碰前A、B两球动量分别是P=10kg·m/s，P=15kg·m/s，碰后动量变化量可能是

A.ΔP=5kg·m/s　　　 ΔP= 5kg·m/s　

B.ΔP=-5kg·m/s　　　ΔP= 5kg·m/s

C.ΔP=5kg·m/s　　　 ΔP= -5kg·m/s

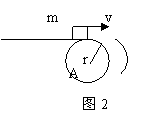D.ΔP=-20kg·m/s　　 ΔP=20kg·m/s

20、如图2所示，m为在水平传送带上被传送

r

的物体，A为终端的皮带轮，半径为r，当m可被

水平抛出时，A轮的每秒转数最少是

A.　　　　 B.　　　　C.　　　 D.

26.(20分)如图3为某一时刻一列简谐横波的部分波形图像。波的传播速度是2.4m/s，在该时刻质点A的速度方向是向上的，求：

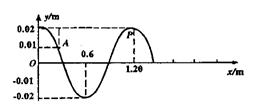（1）波向哪个方向传播？介质质

点的振动周期多大？

（2）质点P从这一时刻起在0.625s

图3

内运动的路程和位移各是多少？

（3）经过0.625s波传播的距离是多少？并画出0.625s后波形图。

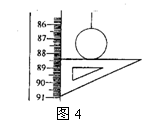
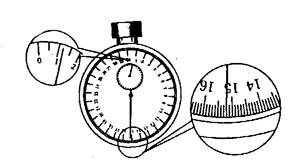
27.（17分）在做“用单摆测定重力加速度”的实验时，用摆长和周期T计算重力加速度的公式是g=_________。如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图4所示，那么单摆摆长是_____。如果测定了40次全振动的时间如图5中秒表所示，那么秒表读数是______s。单摆的摆动周期是_______s。

			图5

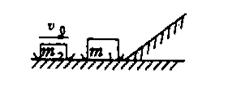
29.（20分）质量为m的物体A置于

倾角为30°，高为h的光滑斜面上底部，

A经轻绳通过光滑定滑轮与质量为2m的

物体B相连接，B套在光滑的直杆上，如

图6

图6所示，开始锁定物体B，使BC绳保

持水平，且BC间距离也为h。然后突然解

除锁定，B将沿杆下滑，B滑至地面与地面撞击后不再弹回，试求：

（1）B与地面撞击的速度v多大？

（2）当B与地面撞击前，绳对物体A所做的功W=？

（3）B触地后，A还能上升多高？

31.（27分）光滑的水平冰面与光滑的倾斜冰面相连，如图7所示，质量为m的大冰车静止在水平冰面上，

另一质量为m的小冰车以速度v滑来，

图7

与大冰车发生正碰，碰后小冰车恰好静止，

大冰车向右滑上倾斜面，上升的最大高度为h。若将大冰车与小冰车的最初位置对调，使大冰车也以速度v去撞击静止的小冰车，撞后小冰车沿倾斜冰面上升的最大高度为h。已知两冰车质量之比m：m=3：1，两次碰撞的机械能损失相同，求两冰车上升的最大高度之比h：h。

物理参考答案及评分意见

（每小题6分）15、B　 16、C　 17、C　 18、A　 19、B　 20、D

26、解：（1）由题设，因质点A的振动方向向上，可判定此波是由左向右传播。　 　　　　　　　　　　　　　　　　　　　　　　　　 (4分)

波长=1.20m，所以T==0.5s　　　　　　　　　　  （各2分）

（2）经t=0.625s，质点P的路程为0.10m，位移为0.02m。（各2分）

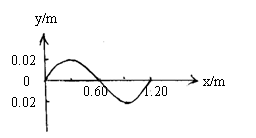（3）经t=0.625s，波传播的距离S=Vt=1.50m　　　　　  （3分）

此时波形图如右图实线.

　　　　　　　　　　　　　　　 （5分）

27、（1）g=(5分)　　　　  （2）87.40m　　　　　  (4分)

（3）75.20s（4分）　　　　（4）1.88s　　　　　　 (4分)

29、解：（1）解除对B的锁定后，B将下滑，因绳作功代数和为零，所以系统机械能守恒。当B触地前，设A上升的高度为h，B下落高度为h，A、B的速度分别为V、V，由速度分解知V=Vcos45°　　　　　 (5分)

由几何知识及三角函数关系知：h=　　　　　　  (3分)

故2mgh=　　　　　　　　　 (3分)

解得：　　　　　　　 (2分)

（2）由功能关系，绳对物体做功W为：W=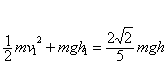(4分)

（3）B触地后，A将上升h，由机械能守恒得：h(3分)

31、解：m撞击m时，水平方向动量守恒，设m碰后速度为

　　　　　　  ,　　(3分)

损失的机械能ΔE= (3分)

m上升的高度为h，由机械能守恒

mgh=　　　　　　　　　 (3分)

m撞击m，撞击后m、m的速度分别为v、v，由动量守恒

mv=mv+ mv　　v= v- v(或= v-)　　 （3分）

损失的机械能ΔE=　　　　　　  （2分）

由题设ΔE=ΔE　（m+m）=0　(3分)

解得：　　　　　　　　　　　　　　　　　 

即：v=v ，　　　　　　　　　 (2分)

当，由，故舍去　 （4分）

即有h：h=1/9　　　　　　　　　　　　　　　　　　 （4分）

若未舍去v，而解出h：h=4：9　　　　　  （扣去4分）