高三物理测练题(八) (电 场)
一、选择题:
1、关于电场强度的叙述,正确的是:
A、沿着电力线的方向,场强越来越小。
B、电场中某点的场强就是单位电量的电荷在该点所受的电场力。
C、电势降落最快的方向就是场强的方向。
D、负点电荷形成的电场,离点电荷越近,场强越大。
2、如果把一个正点电荷放在一电场中,无初速地释放,在点电荷的运动过程中,
A、点电荷运动的轨迹一定与电力线重合。
B、正电荷的加速度方向,始终与所在点的电力线的切线方向一致。
C、点电荷的速度方向,始终与所在点的电力线的切线方向一致。
D、点电荷的总能量越来越大。
3、匀强电场的场强E=5.0×103伏/米,要使一个带电量为3.0×10-15库的负点电荷沿着与场强方向成60°角的方向作匀速直线运动,则所施加外力的大小和方向应是:
A、1.5×10-11牛,与场强方向成120°角。
B、1.5×10-11牛,与场强方向成60°角。
C、1.5×10-11牛,与场强方向相同。
D、1.5×10-11牛,与场强方向相反。
4、两个相同的金属球A和B,A带正电,B带负电,且QA与QB的大小之比是4∶1,若在A、B连线上的某点C放一个点电荷QC,A、B对QC作用的静电力刚好平衡,则
A、C点一定在连线的B点的外侧;
B、C点一定在连线的A点的外侧;
C、C点一定在A、B之间;
D、C点的场强一定为零。
5、在电场中,任意取一条电力线,电力线上的a、b两点相距为d, 则
![]()
![]()
|
|
B、a点电势一定高于b点电势;
|
D、a、b两点间电势差在数值上等于单位正电荷由a点沿任意路径移到b点的过程中,电场力做的功。
6、负电荷q绕某一固定的正电荷作半径为r的匀速圆周运动时必须具有V的线速度,如果再增加负电荷的电量至2q,并使轨道半径变为2r,那么此负电荷的
A、速度不变,周期变大。 B、速度不变,周期不变。
C、速度增至![]() V,周期变大。 D、速度增至2V,周期不变。
V,周期变大。 D、速度增至2V,周期不变。
7、一个正电荷从无穷远处移入电场中的M 点,电场力做功8.0×10-9焦耳,若将另一个等量的负电荷从无穷远处移入同一电场中的N点,必须克服电场力做功9.0×10-9焦耳,则M、N两点的电势大小的关系是:
A、![]() B、
B、![]()
C、![]() D、
D、![]()
8、某带电粒子仅在电场力作用下由A点运动到B点,电力线、粒子在A点的初速度以及运动轨迹如图所示。由此可以判定:
|
 |
A、粒子在A点的加速度大于它在B点的加速度;
B、粒子在A点的动能小于它在B点的动能;
C、粒子在A点的电势能小于它在B点的电势能;
D、A点的电势低于B点的电势。
9、有两个平行板电容器,它们的电容之比为3∶2,所带电量之比为2∶1,平行板间的距离之比为3∶1,如果有两个电子分别从这两个电容器的负极板到达正极板,则这两个电子的动能增量之比是:
A、3∶1 B、4∶3
C、2∶1 D、条件不足,无法确定。
 10、一个质量为m,带电量为q的粒子从两平行板的正中间沿与匀强电场相垂直的方向射入如下图(忽略重力的影响)。当粒子的入射速度为V时,它恰好能穿过电场而不会碰到金属板,现要使入射速度为V/2的带电粒子(质量为m)也恰好能穿过电场而不碰到金属板,则在其它量不变的情况下,必须:
10、一个质量为m,带电量为q的粒子从两平行板的正中间沿与匀强电场相垂直的方向射入如下图(忽略重力的影响)。当粒子的入射速度为V时,它恰好能穿过电场而不会碰到金属板,现要使入射速度为V/2的带电粒子(质量为m)也恰好能穿过电场而不碰到金属板,则在其它量不变的情况下,必须:
A、使粒子的带电量减小为原来的1/2;
B、使两极板间的电压减小为原来的1/2;
C、使两极板间的距离增大为原来的4倍;
|
11、如右图所示,一负电荷在电场中沿某一电力线从A点移到B点,在此过程中不可能出现的情况是:
|
|
![]()
![]()
![]() C、电荷的速度不断变大。
C、电荷的速度不断变大。
D. 电荷的电势能不断减小。
12、如图有两个完全相同的金属球a、b,b固定在绝缘地板上,a
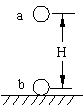 在离b高H的正上方,由静止释放与b发生碰撞后回跳高度为h。设碰撞中无动能损失,空气阻力不计,则:
在离b高H的正上方,由静止释放与b发生碰撞后回跳高度为h。设碰撞中无动能损失,空气阻力不计,则:
A、若a、b带等量同种电荷,则H>h ;
B、若a、b带等量同种电荷,则H<h ;
C、若a、b带等量异种电荷,则H<h ;
D、若a、b带等量异种电荷,则H=h 。
 13、三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电力线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如右图所示,下面判断正确的是:
13、三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电力线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如右图所示,下面判断正确的是:
A、落在a点的颗粒带正电,C点的带负电,b点的不带电。
B、落在a、b、c点颗粒在电场中的加速度的关系是aa>ab>ac。
C、三个颗粒在电场中运动中所受冲量关系是Ia>Ib>Ic。
D、电场力对落在b点的颗粒不做功。
|
|
|
14、平行板电容器一个极板和静电计相接,当该极板带上一定量电荷后,静电计张开一定角度θ,如下图所示。如果平行板电容器发生变化,下面静电计张角θ变化的说法正确的是:
A、两极板间距离增大,θ增大。
B、两极板正对面积减小,θ减小。
C、在电容器内加入电介质,θ增大。
D、上述说法都不对。
|
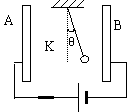 A. 保持K闭合, A板向B板靠近, 则θ增大.
A. 保持K闭合, A板向B板靠近, 则θ增大.
B. 保持K闭合, A板向B板靠近, 则θ不变.
C. 断开K, A板向B板靠近, 则θ增大.
D. 断开K, A板向B板靠近, 则θ不变.
 16、在场强为E,方向水平向左的匀强电场中,一根绝缘细线一端固定在O点,另一端系一个质量为m,带有电量为q的正电荷小球。将悬线拉到水平位置如图所示,由静止释放小球,则小球摆到最低点位置时,细线对小球的拉力大小可能等于:
16、在场强为E,方向水平向左的匀强电场中,一根绝缘细线一端固定在O点,另一端系一个质量为m,带有电量为q的正电荷小球。将悬线拉到水平位置如图所示,由静止释放小球,则小球摆到最低点位置时,细线对小球的拉力大小可能等于:
A、mg B、3mg-2qE C、0 D、qE
班级: 姓名: 坐号: 成绩:
请把选择题答案填在下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|
|
二、实验题:
17、某学生测绘出的电场等势线某部分如图所示,已知图中左、右两边电极分别接直流电源的正、负极,试画出电力线图(不少于3条电力线,并要求标明正、负点电荷)
18、在“电场中等势线的描绘”实验中,下列说法正确的是:
A、这是一个模拟实验,正负电极模拟正负电荷。
B、电源应为6—8伏直流电。
C、当灵敏电流计的示数为零时,两探针接触点在同一等势面上。
|
三、填空题:
 19、如图,QA=2×10-8库,QB=--2×10-8库,A、B相距3厘米,在水平方向的外电场作用下,A、B保持静止,等长的悬线都沿竖直方向,则外电场的场强大小为
,方向 ;A、B中点处总电场的场强大小为 。
19、如图,QA=2×10-8库,QB=--2×10-8库,A、B相距3厘米,在水平方向的外电场作用下,A、B保持静止,等长的悬线都沿竖直方向,则外电场的场强大小为
,方向 ;A、B中点处总电场的场强大小为 。
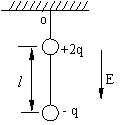 20、在场强为E,方向竖直向下的匀强电场中,有两个质量均为m的带电小球,电量分别为+2q和-q,两小球用长为l的绝缘细线相连,另用绝缘细线系住带正电的小球悬挂于O点而处于平衡状态,如图所示。重力加速度为g,细线对悬点O的作用力等于 。
20、在场强为E,方向竖直向下的匀强电场中,有两个质量均为m的带电小球,电量分别为+2q和-q,两小球用长为l的绝缘细线相连,另用绝缘细线系住带正电的小球悬挂于O点而处于平衡状态,如图所示。重力加速度为g,细线对悬点O的作用力等于 。
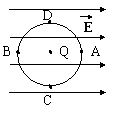 21、在场强为E的匀强电场中,固定一个电量为Q的点电荷。以Q为圆心画一个圆,A、B为过圆心并平行于电力线的两个端点。C、D为过圆心并垂直电力线的直径的两个端点,如图所示。已知A点的电场强度为零,则B点的电场强度的大小是 ;C点的电场强度大小为 。
21、在场强为E的匀强电场中,固定一个电量为Q的点电荷。以Q为圆心画一个圆,A、B为过圆心并平行于电力线的两个端点。C、D为过圆心并垂直电力线的直径的两个端点,如图所示。已知A点的电场强度为零,则B点的电场强度的大小是 ;C点的电场强度大小为 。
22、一个带正电的质点,电量q=2×10-9库仑,在静电场中由a点移到b点,在这过程中,除电场力外,其他力作的功为6.0×10-5焦耳,质点的动能增加了8.0×10-5焦耳,则a,b两点间的电势差Ua-Ub为 。
23、甲和乙两个点电荷相距L,处在光滑绝缘平面上。在库仑力的作用下它们由静止开始运动,开始运动时,甲的加速度为a, 乙的加速度为4a,乙的质量为m。经过一段时间后,乙的加速度变为a,速度为v,这时两个电荷相距 ,甲点电荷的速度大小为 。
24、电子的质量为m,电量为e,以速率V射入匀强电场中,V的方向和场强E的方向相同,设电子刚进入场区时电势能为零,则电子进入场区深 时,其动能和电势能相等。
|
四. 计算题:
|
|
25、如图所示,一条长为L的细线,上端固定,下端拴一质量为m的带电小球。将它置于一匀强电场中,电场强度大小为E,方向是水平的。已知当细线离开竖直位置的偏角为α时,小球处于平衡。
①小球带何种电荷?求出小球所带的电量;
②如果使细线的偏角由α增大到φ,然后将小球由静止开始释放,则φ应为多大,才能使在细线到达竖直位置时小球的速度刚好为零?(提示:![]() )
)
 26、有一匀强电场,其场强为E,方向竖直向下。把一个半径为r的光滑绝缘环,竖直置于电场中,环面平行于电力线,环的顶点A穿有一个质量为m、电量为q(q>0)的空心小球,如图所示。当小球由静止开始从A点下滑到最低点B时,小球受到环的压力多大?
26、有一匀强电场,其场强为E,方向竖直向下。把一个半径为r的光滑绝缘环,竖直置于电场中,环面平行于电力线,环的顶点A穿有一个质量为m、电量为q(q>0)的空心小球,如图所示。当小球由静止开始从A点下滑到最低点B时,小球受到环的压力多大?
|
|
27、充电后的平行板电容器水平放置,两极板间距离10厘米。距下板4厘米处有一质量m=0.01克的不带电小球由静止落下。小球和下极板碰撞间带上了1.0×10-9库的电荷,反跳的高度为8厘米,这时下板所带电量为1.0×10-6库。如果小球和下板碰撞时没有机械能损失,试求该电容器电容多大? (取g=10米/秒2)
|
28、一电子电量为e、质量为m,经电压U加速后,垂直场强方向射入一匀强电场,已知产生偏转电场的平行金属板长为L、场强为E。若电子能够离开偏转电场,求电子刚离开偏转电场时速度的大小和方向。
高三物理测练题(八)参考答案
一. 单选题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| CD | B | C | AD | BD | A | A | B |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| B | D | D | C | BD | A | AD | ABD |
|
|
二、实验题:
(17)如右图所示。
(18)A、B、C、D
三、填空题:
(19) 2×105牛/库,水平向左;1.4×106牛/库。
(20) 2mg+qE (21) 2E; ![]() (22) 1.0×104伏
(22) 1.0×104伏
(23) 2L; V/4 (24) ![]()
三. 计算题:
(25)
|
|
解: ①小球带正电荷. 作出小球的受力图如右图所示, 由图可得:
![]() ①
①
∴ 小球所带电量为
![]() .
.
②根据动能定理, ![]() ②
②
把①式代入②式, 得 Φ=2α
(26)
解: 设小球到达B点时的速度为V, 由动能定理得
![]() ①
①
在B点处由牛顿第二定律得
![]() ②
②
联立①和②式, 解得小球在B点受到环的压力为:
![]()
(27)
解: 设电容器的电容为C, 两极板间的距离为d, 电压为U.
小球下落与板碰撞前瞬间的速度为V, 由机械能守恒得:
![]() ①
①
小球碰撞时没有机械能损失, 所以碰撞后将以速率V竖直向上运动. 由动能定理得:
![]() ②
②
其中
![]() ③
③
联立①、②和③式, 解得
![]()
(28)
解: 设电子离开加速电场时的速度为V1, 则有
![]()
电子离开偏转电场时沿电场力方向的分加速度V2为
![]()
电子离开偏转电场的速度V的大小为:
![]()
其方向与V1方向间的夹角θ为:
![]()
|