北　京　四　中

年　　级：高　三　　　科　　目：物　理　　　编稿老师：厉璀琳

审稿老师：厉璀琳　　　责 　 编：张丽刚

高三物理基础训练5

1．  在x轴上，x=0处放置一个电荷为+4Q的点电荷，x=9cm处放置一个电荷为-Q的点电荷，（1）合场强为零的点的坐标为　　　　  。

（2）在x轴上合场强的方向沿x轴正方向的区域是　　　　 。

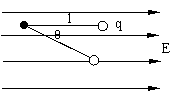
2．如图所示，在水平向右场强为E的匀强电场中，一根长为l的绝缘绳一端固定，另一端拴一带有电荷量+q的小球。现将带电小球拉至绳沿水平位置由静止释放，在球摆至绳与水平方向成θ角的过程中，克服电场力所做的功为　　　　　　 。

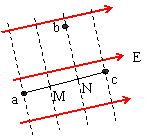
3.如图所示，a、b、c为一匀强电场中的三个点，其中a点电 势为16V,b点电势为4V,c点电势为-2V 。试画出a、b、c三点所在的等势面和该匀强电场电场线的分布。

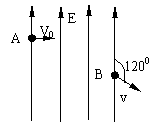
4.如图所示，质量为m，电量为e的电子，从A 点以速度v₀垂直场强方向射入匀强电场中，从B点射出电场时的速度方向与电场线成120 ^o角。求A、B两点间的电势差。

5．如图所示，在一块足够大的铅板A的右侧固定着一小块放射源P,P向各个方向放射β射线，速率为10⁷m/s。在A 板右方距离为2cm处放置一与a平行的金属板B 。在B、A 间加直流电压，板间匀强电场的场强为E=3.64×10⁴N/C，已知β粒子的质量m=9.1×10^-31Kg，电量e=-1.6×10^-19C 。求β粒子打在B板上的范围。

6．如图所示，A、B两块平行带电金属板，A板带正电，B 板带负电并与地连接，有一带电微粒在两板间P点处静止不动。现将B板上移到虚线处，则P 点的场强　　　　 ，P点的电势　　　　  ，带电微粒的电势能　　　　　 　。

7．把一个满偏电流为1mA、内电阻为600Ω的电流表头改装成量程为3A的电流表，则需要　　 联一个　　　　  Ω的电阻；若将这个表头改装成量程为6V的电压表，则应

　　　　 联一个　　　　  Ω的电阻。

8．在如图所示的电路中，A 、B为分压器的输出端，若将变压器的滑动头放在变阻器的中央，则

A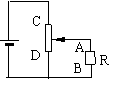． 空载时输出电压为U_AB=U_CD/2

B． 接上负载R时，输出电压U_AB<U_CD/2

C． 负载R的阻值越大，U_AB越接近U_CD/2

D．负载R的阻值越小，U_AB越接近U_CD/2

9．在如图所示的电路中，A、B为相同的两个灯泡，当变阻器的滑动头向D端滑动时

A． A灯变亮，B灯变暗

B． A灯变暗，B灯变亮

C． A　、B灯均变亮

D．A　、B灯均变暗

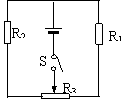
10．在如图所示的电路中，已知电源 的电动势为6.3V,内电阻为0.5Ω,R₁=2Ω,R₂=3Ω,

R₃=5Ω 。闭合开关S，调节滑动变阻器的滑动头，求通过电源的电流范围。

11．如图所示，电阻R₁=8Ω，直流电动机的内电阻R₂=2Ω,当电键S断开时，电阻R₁消耗的电功率为2.88W，电源的效率为80%，当电键S接通后，电阻R₁消耗的电功率为2W，试求电键接通后，电动机输出的机械功率。（除电动机内阻外其它损耗不计）

12．如图所示的电路中，电池的电动势E=5V，内电阻r=10Ω，固定电阻R=90Ω,R₀是可变电阻，在R₀由零增加到400Ω的过程中，求：（1）可变电阻R₀上消耗热功率最大的条件和最大热功率。（2）电池的内电阻r 和固定电阻R 上消耗的最小热功率之和。

13．如图所示，E=10V，R₁=4Ω,R₂=6Ω,C=30μF ，电池内电阻可以忽略。（1）闭合开关S，求稳定后通过R₁的电流。（2）然后将开关S断开，求这以后流过R₁的总电量。

答案：

1．（1）（18，0）cm（2）0<x<9cm或x>18cm　　

2．

3．连接ac，将ac三等分，则三等分点M和N的电势分别等于10V和4V。连接bN，则bN表示等势面，电势等于4V，过a和c分别做bN的平行线，得到过a，c的等势面。再作有向直线垂直bN，如图红线表示，则为匀强电场的方向。

4．U_AB=－mv₀²/6q

5．半径为r =2.5cm的圆内。

6．P点的场强不变，P点电势变小，电荷在P点的电势能变小。

7．改装成电流表：并联一个0.20Ω的电阻；改装成电压表：串联一个5400Ω的电阻。

8．ABC

9．D

10．2.1A~3A

11．1.5W

12．（1）0.0625W　　（2）P_min=0.01W

13．（1）闭合S，I=1A （2）Q=1.2×10^-4C

提示：

4．v_B=v₀/cos30^o，则由A到B：qU_AB=

5．解：初速度方向平行于金属板的β粒子打得最远。设d=2cm

d=　 ①　  r = v₀t　　　②　　解①②

6．∵静止不动，∴带负电。

电容器带电量Q一定，∵ E=，

∴B上移，E不变；U_P－U_B=U_P=E∣BP∣变小；电势能－qU_P变大。

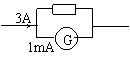
7．改装成电流表时，如图：。

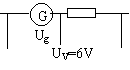同理改装成电压表时，如图：

9．当滑片向D端滑动时，则滑动变阻器接入电路电阻减小，则会导致总电阻变小，总电流变大，路端电压U变小，U_A=U，A灯变暗，同时A的电流变小，所以与A并联的部分电路电流会变大，R分压变大，而U是变小的，所以U_B会变小，B灯变暗。

　　　 10．解：设滑动变阻器与R₁并联部分的电阻为R_右可推导出总电阻表达式：

R­_总=

当R_右=3Ω时，R_总max=3Ω，此时I_min=2.1A

当R_右=0时，R_总min=2.1Ω，此时I_max=3A

11．S断开时，　　得：U₁=4.8V，I₁=0.6A

　　　 　　　　 U₁=ε－I₁r　　　　　 　　 即：4.8= ε－0.6r　　 ①

电源效率：　　　　　　　　　　　　　 ②

∴ε =6V，r = 2Ω

S闭合后，　　　　得：U₂=4V，I₂=0.5A

　　　　　　　　　　 U₂= ε－I_总r　　　　　　　　   得：I总=1A　

电动机的电压为U₂=4V，电流为I′=I-I₂=0.5A

则电动机总功率为：P=U₂I′=2W　　　　　　　　　 热损耗为：P_损=

∴输出机械功率为：P－P_损=1.5W

12．（1）当R₀=R+r时，P_max=

　　　 （2）P=，当R₀=400Ω时，P_min=0.01W

13

（1）闭合S，稳定后，R₁和R­₂串联，通过R₁的电流为I=

（2）断开s前，电容器的电压：U=IR₂=6V

　　 断开s后，电容器的电压：E=10V

∴Q=（E-U）C=1.2×10^-4库。

北　京　四　中

年　　级：高　三　　　科　　目：物　理　　　编稿老师：厉璀琳

审稿老师：厉璀琳　　　责 　 编：张丽刚

北京四中物理基础训练6

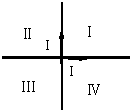
1．有两条垂直交叉但不接触的直导线，通以大小相等的电流，方向如图所示，则哪些区域中某些点的磁感应强度可能为零　　　　　　　　　　　　　　  （　　　　）

A．区域Ⅰ　　　　　　　　　  B.区域Ⅱ

C．区域Ⅲ　　　　　　　　　　 D.区域Ⅳ

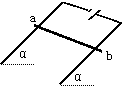
2．如图所示，两根相距l平行放置的光滑导电轨道，倾角均为α，轨道间接有电动势为E的电源（内阻不计）。一根质量为m、电阻为R的金属杆ab, 与轨道垂直放在导电轨道上，同时加一匀强磁场，使ab杆刚好静止在轨道上。求所加磁场的最小磁感应强度B的大小为　　　　　 。（轨道电阻不计）

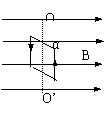
3．如图所示,在水平匀强磁场中，有一匝数为N，通有电流I的矩形线圈，线圈绕oo’轴转至线圈平面与磁感线成α角的位置时，受到的安培力矩为M，求此时穿过线圈平面的磁通量。

4．氘核（）、氚核（）、氦核（）都垂直磁场方向射入同一足够大的匀强磁场，求以下几种情况下，他们的轨道半径之比及周期之比是多少？（1）以相同的速率射入磁场；（2）以相同动量射入磁场；（3）以相同动能射入磁场。

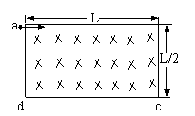
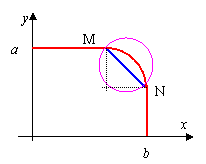
5．如图所示，矩形匀强磁场区域的长为L，宽为L/2。磁感应强度为B，质量为m，电量为e的电子沿着矩形磁场的上方边界射入磁场，欲使该电子由下方边界穿出磁场，求：（1）电子速率v的取值范围？

（2）电子在磁场中运动时间t的变化范围。

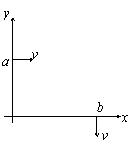
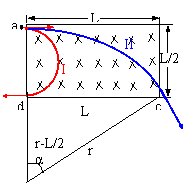
6．如图所示，一带电质点，质量为m₁；电量为q，以平行于ox轴的速度v从y轴上的a点射入图中第一象限所示区域，为使该质点能从x轴上b点以垂直于ox轴的速度v射出，可在适当地方加一个垂直于xy平面，磁感应强度为B的匀强磁场，若此磁场仅分布在一个圆形区域内，试求这个圆形磁场区域的最小半径、重力忽略不计。

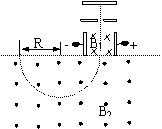
7．如图所示为一台质谱仪的结构原理图，设相互正交的匀强电、磁场的电场强度和磁感应强度分别为E和B₁，则带电粒子在场中做匀速直线运动，射出粒子速度选择器时的速度为v=　　　 ,该粒子垂直另一个匀强磁场B₂的边界射入磁场，粒子将在磁场中做轨迹为半圆的匀速圆周运动，若测得粒子的运动半径为R，求粒子的荷质比q/m。

8．在高能物理研究中，粒子回旋加速器器起着重要作用。如图所示，它由两个铝制D形盒组成。两个D形盒处在匀强磁场中并接有正弦交变电压。下图为俯视图。S为正离子发生器。它发出的正离子（如质子）初速度为零，经狭缝电压加速后，进入D形盒中。在磁场力的作用下运动半周，再经狭缝电压加速。如此周而复始，最后到达D形盒的边缘，获得最大速度（动能），由导出装置导出。

已知被加速质子，质量m=1.7×10^-27Kg，电量q=1.6×10^-19C，匀强磁场的磁感应强度B=1T，D形盒半径R=1m。

（1）为了使质子每经过狭缝都被加速，正弦交变电压的频率为　　　　　　　 。

（用字母表示）

（2）使质子加速的电压应是正弦交变电压的　　　　　　　　　  值。

（3）试计算质子从加速器被导出时，所具有的动能是多少电子伏。

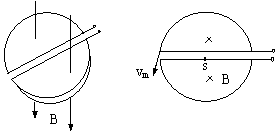
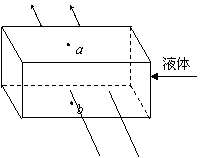
9．如图所示为一个电磁流量计的示意图，截面为正方形的磁性管，其边长为d，内有导电液体流动，在垂直液体流动方向加一指向纸里的匀强磁场，磁感应强度为B。现测得液体a、b两点间的电势差为U,求管内导电液体单位时间的流量Q。

10．如图，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝a、b、c和d，外筒的外半径为r₀。在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为B，在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场。一质量为m、带电量为+q的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零。如果该粒子经过一段时间的运动之后恰好又回到出发点S，则两极之间的电压U应是多少？（不计重力，整个装置在真空中。）

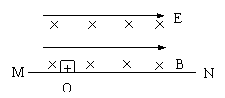 11．如图所示，在水平向右的匀强电场E和水平向里的匀强磁场B并存的空间中，有一个足够长的水平光滑绝缘面MN。面上O点处放置一个质量为m，带正电q的物块，释放后物块自静止开始运动。求物块在平面MN上滑行的最大距离。

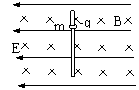12．如图所示，在场强为E方向水平向左的匀强电场和磁感应强度为B垂直纸面向里的匀强磁场区域内，固定着一根足够长的绝缘杆，杆上套着一个质量为m，电量为q的小球，球与杆间的动摩擦因数为μ。现让小球由静止开始下滑，求小球沿杆滑动的最终速度为多大？

答案：

　　　 1．AC　　2．　　 3．　

4．（1）半径之比：2:3:2　 周期之比：2:3:2
　　　 　（2）半径之比：2:2:1　 周期之比：2:3:2

　（3）半径之比：　周期之比：2:3:2

5．（1）　　 （2）0.29（或：）

6．　　　　　7．v=E/B₁，荷质比：E/B₁B₂R

8．（1）qB/2πm　（2）瞬时值　　　　（3）4.7×10⁷eV

9．Q=　　　　　10．　　　　　11．S=　　　　 12．v=

提示：

1．只有第一、三象限，两电流产生的磁场是反向的。

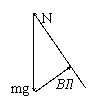
2．如图，重力，导轨对它的支持力，以及磁场的安培力三者顺次连接构成力三角。

　　　 3．如图从上方俯视图：

M =NBIScosα

　　　 　φ=Bssinα　　  得到答案φ=Mtgα/NI

4．利用　 可得

5．如图：

情况I中，r =　　 ∴

情况II中，　∴

则要使电子从下方边界穿出磁场，则：

　　得到r = 1.25L

情况I中，t = T/2=　　

情况II中，圆心角α=53^o　　 t =

所以时间　0.29

6．如图，红色曲线表示电荷的运动轨迹，其中

它在磁场中的轨迹为一段圆弧，其中MN是圆形磁场的弦，则要使圆形磁场的面积最小，则MN是圆形磁场直径即如图黄色圆。则此时R=MN/2==

7．速度选择器：只让速度满足：　 即：v =

利用R=mv/qB₂　 可得荷质比。

8．（1）正弦交变电压的频率等于带电微粒在匀强磁场中的频率。（加速的时间与在磁场中偏转的时间相比值可忽略不计）

　（2）加速电压应是正弦交变电压的瞬时值。不同瞬时差值，加到最大速度所用的时间不同。

（3）当它从回旋加速器中出来时，轨道半径等于D形盒的半径。

由： R=mv/qB

　　可以得到= 4.7×10⁷eV

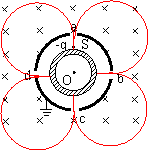9．注意a和b分别表示上、下表面的两点。在洛仑兹力作用下，电荷在上下表面聚集，因此上下表面间形成匀强电场，具有一定电势差。此后电荷受到电场力和洛化兹力，当qE=qvB时，电势差恒定。

10．如图轨迹。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

11．当物块受到向上的洛仑兹力等于重力时，物块会开始飞离地面。

此时　　　　 qvB=mg　　 

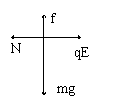再由动能定理：qEs=　　可解。

12．

初始：小球受力如图，加速

随着速度增加，小球受到向左的洛仑兹力，则N会减小，减小，则加速度a增大，小球做a增加的加速运动；

当qvB=qE时，N=0，f=0，加速度a_max=g

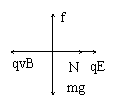此后速度继续增大，洛仑摩擦力qvB>qE，则杆的支持力N反向向右，并增大，摩擦力f也随之增加，物体加速度减小，但仍加速，

直到当加速度a=0时，物体匀速运动。

此时：f = mg

　　  f = μN

qvB=qE+N

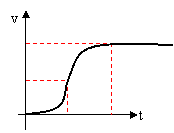 解以上各式即可。

小球运动的v-t图象如图所示：