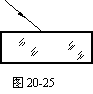高三物理光的反射和折射

提高测试

一、选择题（每小题3分，共30分）

1．关于影子下列说法中正确的是 （　　　）

A．一点光源在物体的一侧，屏在物体的另一侧，则点光源离物体越近，屏离物体越远，所形成的影子就越大

B．发光体在不透明的物体背面必然产生一个暗度均匀的影子

C．一个点光源在不透明物体的后面产生的影子，只有本影区，没有半影区

D．在地球上不同的区域，可能同时观察到日全食和日环食

2．如图20-11所示，竖直墙壁前有一固定点光源S，从这点光源处水平抛出的物体在竖直墙壁上的影子运动情况是 （　　  ）

A．匀速直线运动　　　B．自由落体运动

C．匀加速直线运动　　D．变加速直线运动

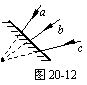
3．如图20-12所示，a、b、c三条光线交于S点，如果在S点前任意位置放置一个平面镜，则三条反射光线（　　 ）

A．可能交于一点也可能不交于一点

B．一定不交于一点

C．交于镜前的一点，成为一实像点

D．它们的延长线交于镜后一点，得到一个虚像点

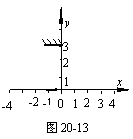
　　4．如图20-13，在竖直的xoy平面上，人眼位于（3，0）坐标点，一平面镜位于图示位置，平面镜两端坐标分别为（－1，3）和（0，3）．一点光源S从坐标原点O沿x轴负方向运动，S在如下哪个区域运动时，人眼能从平面镜中看到S点的像 （　　  ）

　　A．0到－1区间　　　 B．－1到－3区间

C．－3到－5区间　　 D．－5到－∞区间

5．某汽车驾驶室外有一用平面镜制作的观后镜，当汽车以50 km/h的速度在公路上向前行驶时，司机从镜中看到车后的静止景物向镜后运动的速度为 （　　  ）

A．50 km/h　　B．25 km/h　　C．100 km/h　　D．0

　　6．一束光由空气入射某介质，入射角为60°，其折射光线恰好与反射光线垂直，则光在该介质中的传播速度为　（　　 ）

A．×10 ⁸ m/s　Ｂ．×10 ⁸ m/s　　Ｃ．×10 ⁸ m/s　 Ｄ．×10 ⁸ m/s

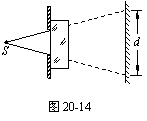
7．点光源S通过带有圆孔的挡板N，照射到屏M上，形成直径为d的亮圆．如果在挡板靠近光屏一侧放上一块厚玻璃砖，如图20-14所示，这时点光源通过圆孔和玻璃，在屏上形成直径为D的亮圆．则直径D和d的大小关系为 （　　 ）

A．d>D　　B．d=D　 C．d<D　　D．无法确定

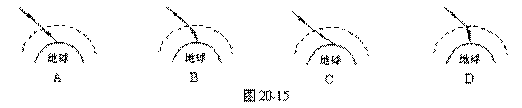
8．大气中空气层的密度是随着高度的增加而减小的．从大气外射来束阳光，如图20-15所示的四个图中，能粗略表示这束阳光射到地面的路径的是 （　　  ）

9．在完全透明的水下某深度处放有一点光源，在水面上可见到一个圆形光斑，如果此圆形光斑的半径在均匀增大，则此时点光源正在 （　　  ）

A．加速上升　 B．加速下沉　 C．匀速上升　 D．匀速下沉

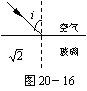　　10．一束光从空气射向折射率n＝的某种玻璃的表面，如图20-16所示．i代表入射角，则 （　　　 ）

　　A．当i > 45°时会发生全反射现象

　　B．无论入射角i是多大，折射角r都不会超过45°

　　C．欲使折射角r＝30°，应以i＝45°的角度入射

　　D．当入射角i＝arctan时，反射光线跟折射光线恰好互相垂直

　　二．填空题（每小题4分，共28分）

1．身高1.6m的人以1m/s的速度沿直线向灯下走去，在某一时刻，人影长为1.8m，经2s后，影长变为1.3m，则这盏路灯的高度应为　　m．

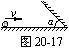　　2．如图20-17，球沿光滑桌面向平面镜运动，要使球在平面镜中的像沿竖直方向向上运动，则平面镜与桌面的夹角α应为　　　 ．　　

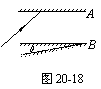
　　3．如图20-18所示，A、B两个平面镜平行放置，一束光线入射A镜，反射后从B镜射出．若保持入射光线不变，而只让B镜转动θ角，则转动后从B镜射出的光线与转动前从B镜射出的光线之间的夹角为　　　　．　

　　

4．如图20-19所示，在三棱镜中BC面镀有反射膜，一束白光斜射入AB面，经棱镜后在屏幕的bc段形成彩色光带，则b点的颜色是　　 色．（屏幕距棱镜的AC面较近且与AC面平行）　

5．如图20-20，玻璃体ABC是截面半径为R的半圆形柱体的一部分，O为圆心，OC＝OB＝R，∠AOB＝60°，折射率n＝2．一束平行光垂直AB面入射玻璃体，在BC弧面上有光线射出的部分其弧长为　　　　．

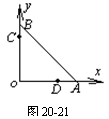
　　6．由某种透光物质制成的等腰直角棱镜ABO，两腰长都是16 cm．为了测定这种物质的折射率，将棱镜放在直角坐标系中，并使两腰与ox、oy轴重合，如图20-21所示．从OB边的C点注视A棱，发现A棱的视位置在OA边D点．在C、D两点插大头针，看出C点坐标位置（0，12）D点坐标位置（9，0），由此可计算出该物质的折射率为　　　　．

　　

　　7．在测定玻璃的折射率的实验中，对一块两面平行的玻璃砖，用“插针法”找出与入射光线对应的出射光线．现有甲、乙、丙、丁四位同学分别做出如20-22所示的四组插针结果． (1)从图上看，肯定把针插错了的同学是　　　　　 ．

　(2)从图上看，测量结果准确度最高的同学是　　　　　　　  ．

　　三、计算题（第4、5小题每题9分，其余每小题8分，共42分）

1．(选做)如图20-23所示，A是直径为10 cm的发光圆盘，B是直径为5 cm的遮光板，C为光屏，三者中心共轴，A、B之间相隔200 cm，当C离B多远时，正好在屏上的本影消失而有半影？这时半影环的半径是多少？本影可取得最大直径是多少？

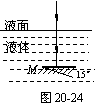
2．如图20-24所示，M是一块平面镜，位于透明液体之中，

镜面水平向上放置，一细束光竖直向下射来，穿过液体射到平面镜上．现将平面镜绕水平轴转动15°角，光线经平面镜反射后在液体与空气的分界的液面处分成两束，测得这两束光线夹角为

105°，求这种液体的折射率．

3．（12分）如图20-25所示，光线从空气斜射入一块两面平行的玻璃砖的一个平面，再从另一平面射出，试证明出射光线与入射光线平行，并说明出射光线相对于入射光线的侧移量．

　　4．（10分）主截面是边长为d的正方形的棱柱，折射率为n，将其弯成半圆形（如图20－26所示）．要使A端垂直入射的光线全部从B端射出，求所弯半圆形的最小内半径R的值．

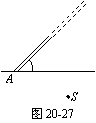
 5．如图20-27所示，某种透明液体的折射率为，在液面下方有一点光源S，液面上方有一无限长的细杆，其与液面夹角为45°，且与液面交于A点．已知A点与点光源S的水平距离大于S在液体中的深度，细杆与S在同一竖直平面内，点光源所发出的光线限制在此竖直平面内．试求点光源发出的光线能照射到细杆上的所有光线在液体中所分布的角度范围为多大．

参考答案

　　

B组

一、

1、AC．　2、A．　 3、C．  4、C．　5、A．　6、A．  7、A．

8、B．　9、D．　10、BCD．

二、

1、8．　2、135°．　3、2θ．　4、红．　5、πR/6．　 6、1.33．

7、（1）乙，（2）丁．

三、

1、2m，10cm，5cm．

2、．

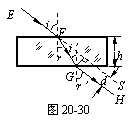
3、证明：如图20-30所示，设玻璃的折射率为n，玻璃砖的厚度为h，在玻璃的上表面的入射角为i，则光线在F点发生折射时有：n=．

根据几何关系可知，光线在G点的入射角为i′= r，出射光线的折射角为r′，则光线在G点发生折射时有：

所以有　，因此 r′= i，即EF∥GH．

出射光相对于入射光的侧移量为：d=FGsin∠GFS．因为FG=，∠GFS= i-r．所以  

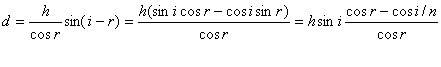
　上式表明，出射光线相对于入射光线发生的侧移量大小与玻璃砖的厚度、入射角及玻璃的折射率有关．

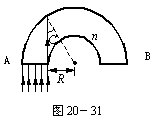
4、要使光线全部由B端射出，则要求射入棱柱的光线全部发生全反射，而不能发生折射．那么从A端入射的光线中，只要使最易发生折射的光线发生全反射，则可满足题目要求．最易发生折射的光线应为入射角最小的光线，由图20-31可看出A端最内侧的光线其入射角最小，因此必须保证此光线能发生全反射，即此光线的入射角等于或大于临界角．由图中的几何关系可看出，此光线入射角的正弦值为：sinC＝R/（R + d）．（由折射定律可知）

由此可解得半圆的最小内半径为R＝d/（n－1）．

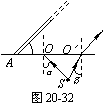
5、如图20-32所示，连SO，由点光源发出的这条光线入射角恰好等于临界角，据可知，α=45°，此光线将照射到杆的A端．

连SO′，设此光线入射角为β，它的折射光线恰好与细杆平行，则，可解得β=30°．

所以照射到细杆上的光线在液体中分布在∠OSO′=75°的范围内．