高三物理典型例题解答(四)
例1、
 如图1,劲度系数为k的轻质弹簧一端固定在墙上,另一端和质量为M的容器连接,容器放在光滑水平的地面上,当容器位于O点时弹簧为自然长度,在O点正上方有一滴管,容器每通过O点一次,就有质量为m的一个液滴落入
如图1,劲度系数为k的轻质弹簧一端固定在墙上,另一端和质量为M的容器连接,容器放在光滑水平的地面上,当容器位于O点时弹簧为自然长度,在O点正上方有一滴管,容器每通过O点一次,就有质量为m的一个液滴落入![]()
![]()
![]() 容
容
器,开始时弹簧压缩,然后撒去外力使容器围绕O点往复运动,
求:
(1)容器中落入n个液滴到落入(n+1)个液滴的时间间隔; L0
(2)容器中落入n个液滴后,容器偏离O点的最大位移。 图1
分析与解:本题中求容器内落入n个液滴后偏离O点的最大位
移时,若从动量守恒和能量守恒的角度求解,将涉及弹簧弹性势能的定量计算,超出了中学大纲的要求,如果改用动量定理和动量守恒定律求解,则可转换成大纲要求的知识的试题。
(1)弹簧振子在做简谐运动过程中,影响其振动周期的因素有振子的质量和恢复系数(对弹簧振子即为弹簧的劲度系数),本题中恢复系数始终不变,液滴的落入使振子的质量改变,导致其做简谐运动的周期发生变化。
容器中落入n个液滴后振子的质量为(M+nm),以n个液滴落入后到第(n+1)个液滴落入前,这段时间内系统做简谐运动的周期Tn=2π![]() ,容器落入n个液滴到(n+1)个液滴的时间间隔△t=Tn /2,所以
,容器落入n个液滴到(n+1)个液滴的时间间隔△t=Tn /2,所以
△t =π![]()
(2)将容器从初始位置释放后,振子运动的动量不断变化,动量变化的原因是水平方向上弹簧弹力的冲量引起的,将容器从静止释放至位置O的过程中,容器的动量从零增至p,因容器位于O点时弹簧为自然长度,液滴在O点处落入容器时,容器和落入的液滴系统在水平方向的合力为零, 根据动量守恒定律, 液滴在O处的落入并不改变系统水平方向的动量,所以振子处从位置O到两侧相应的最大位移处,或从两侧相应在的最大位移处到位置O的各1/4周期内,虽然周期Tn和对应的最大位移Ln在不断变化,但动量变化的大小均为△p=p-0=p,根据动量定理可知识,各1/4周期内弹力的冲量大小均相等,即:
F0(t)·T0/4 = Fn(t)·Tn/4
其中T0是从开始释放到第一次到O点的周期,T0=2π![]() 。Tn是n个液滴落入后到(n+1)个液滴落入容器前振子的周期,Tn=2π
。Tn是n个液滴落入后到(n+1)个液滴落入容器前振子的周期,Tn=2π![]() 。而F0(t)和Fn(t)分别为第一个1/4周期内和n个液滴落入后的1/4周期内弹力对时间的平均值,由于在各个1/4周期内振子均做简谐运动,因而弹力随时间均按正弦(或余弦)规律变化,随时间按正弦(或余弦)变化的量在1/4周期内对时间的平均值与最大值之间的关系,可用等效方法求出,矩形线圈在匀强磁场中匀速转动时,从中性而开始计地,产生的感应电动势为ε=εmsinωt= NbωSsinωt。ε按正弦规律变化,根据法拉第电磁感应定律ε=N
。而F0(t)和Fn(t)分别为第一个1/4周期内和n个液滴落入后的1/4周期内弹力对时间的平均值,由于在各个1/4周期内振子均做简谐运动,因而弹力随时间均按正弦(或余弦)规律变化,随时间按正弦(或余弦)变化的量在1/4周期内对时间的平均值与最大值之间的关系,可用等效方法求出,矩形线圈在匀强磁场中匀速转动时,从中性而开始计地,产生的感应电动势为ε=εmsinωt= NbωSsinωt。ε按正弦规律变化,根据法拉第电磁感应定律ε=N![]() ,ε在1/4周期内对时间的平均值ε=2εm/π。这一结论对其它正弦(或余弦)变化的量对时间的平均值同样适用,则有
,ε在1/4周期内对时间的平均值ε=2εm/π。这一结论对其它正弦(或余弦)变化的量对时间的平均值同样适用,则有
F0(t)=2kL0/π,Fn(t)=2kLn/π
代入前式解得:Ln=![]() L0
L0
例2、利用压缩空气贮气瓶给汽车轮胎充气,贮气瓶容积是15L,轮胎容积是10L,贮气瓶中气体压强是12atm,温度为300K,轮胎内原有空气压强是5atm,温度为320K,设在充气过程中,贮气瓶与轮胎温度各自保持不变,问当轮胎内的空气压强增加到8atm时,贮气瓶中的气体压强为多少个大气压?(设充气过程中轮胎容积不变)
分析与解:这是一道典型的变质量气体连接问题,在充气过程中,贮气瓶中气体将进入轮胎内,轮胎与贮气瓶都是变质量系统,本题的关键是如何改变质量为定质量,从纲外绕回纲内。

 设贮气瓶中气体初、末压强分别为P1、P2,轮胎内气体初、末压强分别为P3、、P4,为了化变为不变,我们可以虚拟如下气体状态变化过程:①瓶中原
设贮气瓶中气体初、末压强分别为P1、P2,轮胎内气体初、末压强分别为P3、、P4,为了化变为不变,我们可以虚拟如下气体状态变化过程:①瓶中原
气体的△V1部分充入轮胎内(如图2),进入轮胎后体积变化△V1';②瓶中气体剩余部分(V1-△V1)膨胀至体积V1;③
轮胎内原有气体从V2压缩至V2',且使(V2'+△V1')=V2,
为了简明直观,可用方框图表示上述虚拟过程。
![]()

![]()
![]()
![]()
![]() P1
P2
P1
P2
P3
P4
P1
P2
P1
P2
P3
P4
![]()
![]()
![]() △V1
△V1'
V1-△V1
V1
V2
V2'
△V1
△V1'
V1-△V1
V1
V2
V2'
T1 T2 T1 T1 T2 T2
根据上述方框图,即可很容易地得到如下方程:
![]() =
=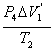 ①
①
P1(V1-△V1)=P2V1 ②
P3V2=P4V2' ③
又V2 =V2'+△V1' ④
联立①②③④解得:
P2=P1=10.125atm
从求解过程可以看出,用虚拟法解题时除了需正确地虚拟物理过程外,还要将虚拟的物理过程用图显示出来,这样可使思维过程表达得更清晰,求解过程更直观
![]()
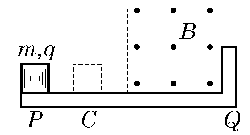
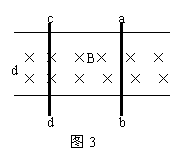
![]() 例3、如图3所示,两根互相平行、间距d=0.4米的金属导轨,水平放置于匀强磁场中,磁感应强度B=0.2T,磁场垂直于导轨平面,金属滑杆ab、cd所受摩擦力均为f=0.2N。两根杆电阻均为r=0.1Ω,导轨电阻不计,当ab杆受力F=0.4N的恒力作用时,ab杆以V1做匀速直线运动,cd杆以V2做匀速直线运动,求速度差(V1- V2)等于多少?
例3、如图3所示,两根互相平行、间距d=0.4米的金属导轨,水平放置于匀强磁场中,磁感应强度B=0.2T,磁场垂直于导轨平面,金属滑杆ab、cd所受摩擦力均为f=0.2N。两根杆电阻均为r=0.1Ω,导轨电阻不计,当ab杆受力F=0.4N的恒力作用时,ab杆以V1做匀速直线运动,cd杆以V2做匀速直线运动,求速度差(V1- V2)等于多少?
分析与解:在电磁感应现象中,若回中的感应电动势是由导体做切割磁感线运动而产生的,则通常用ε=BlVsinθ来求ε较方便,但有时回路中的电动势是由几根棒同时做切割磁感线运动产生的,如果先求出每根导体棒各自的电动势,再求回路的总电动势,有时就会涉及“反电动势”而超纲。如果取整个回路为研究对象,直接将法拉第电磁感应定律ε=![]() 用于整个回路上,即可“一次性”求得回路的总电动势,避开超纲总而化纲外为纲内。
用于整个回路上,即可“一次性”求得回路的总电动势,避开超纲总而化纲外为纲内。
cd棒匀速向右运动时,所受摩擦力f方向水平向左,则安培力Fcd方向水平向右,由左手定则可得电流方向从c到d,且有:
Fcd = IdB = f
I = f /Bd ①
取整个回路abcd为研究对象,设回路的总电势为ε,由法拉第电磁感应定律ε=![]() ,根据B不变,则△φ=B△S,在△t时间内,
,根据B不变,则△φ=B△S,在△t时间内,
△φ=B(V1- V2)△td
所以:ε=B(V1- V2)△td/△t=B(V1- V2)d ②
又根据闭合电路欧母定律有:
I=ε/2r ③
 由式①②③得:V1- V2 = 2fr / B2d2
由式①②③得:V1- V2 = 2fr / B2d2
代入数据解得:V1- V2 =6.25(m/s)
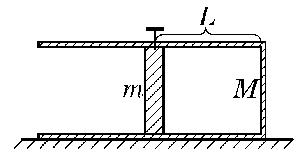
例4、如图4所示,轻质弹簧上端悬挂在天花板上,下端连接一个质量为M的木板,木板下面再挂一个质量为m的物体,当拿去m后,木板速度再次为零时,弹簧恰好恢复原长,求M与m之间的关系?
分析与解:按常规思路,取M为研究对象,根据动能定理或机械能守恒定律求解时,涉及弹力(变力)做功或弹性势能的定量计算,超出了中学教材和大纲的要求。
考虑到拿去m后,M将做简谐运动,则拿去m时M所处位置,与弹簧刚恢复原长时M所处位置分别为平衡位置两侧的最大位置处,由M做简谐运动时力的对称性可知,在两侧最大位移处回复力的大小应相等,在最低位置处F=mg,方向向上,在最高位置处F=Mg,方向向下,所以有M=m。
例5.假设在质量与地球质量相同、半径为地球半径两倍的某天体上进行运动比赛,那么与在地球上的比赛成绩相比,下列说法中正确的是[A ]
①跳高运动员的成绩会更好
②用弹簧秤称体重时,体重数值会变得更小
③投掷铁钅并的距离会更远些
④用手投出的篮球,水平方向的分速度会变大
A.①②③ B.②③④ C.①③④ D.①②④
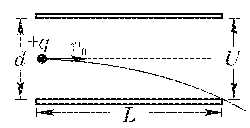
例6.如图5所示,带正电的粒子以一定的初速度v0沿中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出,已知板长为L,板间的电压为U,带电粒子的带电量为q,粒子通过平行金属板的时间为T,不计粒子的重力,则[B ]
|
|
| 图5 |
A.粒子在前T/2时间内,电场力对粒子做功为(1/4)qU
B.粒子在后T/2时间内,电场力对粒子做功为(3/8)qU
C.粒子在下落前d/4和后d/4内,电场力做功之比为1∶2
D.粒子在下落前d/4和后d/4内,通过的时间之比为1∶3
例7.如图6所示,一列简谐横波在x轴上传播,某时刻的波形如图所示,关于波的传播方向与质点a、b的运动情况,下列叙述中正确的是[D ]
|
|
| 图6 |
A.若波沿x轴正方向传播,a运动的速度将减小
B.若波沿x轴正方向传播,a运动的速度将保持不变
C.若波沿x轴负方向传播,b将向+y方向运动
D.若波沿x轴负方向传播,b将向-y方向运动
例8.对于宇宙的形成,在当代占主要地位的看法是:我们的宇宙诞生于150亿~200亿年前的一次大爆炸,其主要依据是[B ]
(1)光谱分析得到的红移现象,即星体离我们远去
(2)天然放射现象
(3)牛顿运动定律
(4)月球运动中的各种现象
A.(1)、(2)
B.(1)、(3)
C.(3)、(4)
D.(2)、(3)
例9.下列说法正确的是[D ]
A.物体在恒力作用下的运动方向是不会改变的
B.加速前进的汽车,后轮所受的摩擦力方向与运动方向相反
C.第一宇宙速度为7.9km/s,因此飞船只有达到7.9km/s才能从地面起飞
D.作用力与反作用力都可以做正功,也可以做负功
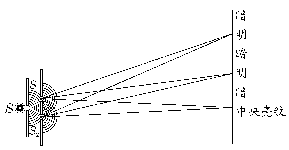
例10.如图7所示,是光的双缝干涉的示意图,下列说法不正确的是[A ]
|
|
| 图7 |
A.单缝S的作用是为了增加光的强度
B.双缝S1、S2的作用是为了产生两个频率相同的线状光源
C.当S1、S2发出两列光的路程差1.5λ时,产生第二暗纹(λ为光的波长)
D.当S1、S2发出两列光的路程差为2λ时,产生第二明纹(λ为光的波长)
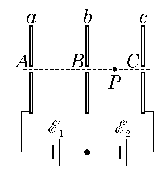
例11.如图8所示,三平行金属板a、b、c接到电动势分别为![]() 1、
1、![]() 2的电源上,已知
2的电源上,已知![]() 1<
1<![]() 2,在A孔右侧有一带负电的质点,由静止释放后向右运动穿过B到达P点后再返回A孔,则[D ]
2,在A孔右侧有一带负电的质点,由静止释放后向右运动穿过B到达P点后再返回A孔,则[D ]
|
|
| 图8 |
A.只将b板右移一小段距离后再释放该质点,质点仍运动到P点后返回
B.只将b板右移一小段距离后再释放该质点,质点将达不到P点
C.只将b板右移稍长距离后再释放该质点,质点能穿过C孔
D.若将质点放在C孔左侧由静止释放,质点将能穿过A孔
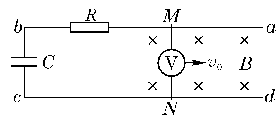
例12.如图9所示,U型线框abcd处于匀强磁场中,磁场的磁感强度为B,方向垂直于纸面向内.长度为L的直导线MN中间串有一个电压表跨接在ab与cd上且与ab垂直,它们之间的接触是完全光滑的.R为电阻,C为电容器,现令MN以速度v0向右匀速运动,用U表示电压表的读数,q表示电容器所带电量,C表示电容器电容.F表示对MN的拉力.设电压表体积很小,其中线圈切割磁感线对MN间的电压的影响可以忽略不计.则[C ]
|
|
| 图9 |
A.U=BLv0 F=v0B2L2/R
B.U=BLv0 F=0
C.U=0 F=0
D.U=q/C F=v0B2L2/R
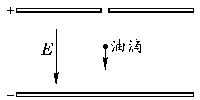
例13.密立根油滴实验如图10所示:在电介质为空气的电容器中,观测以某速度送入的一个油滴,这油滴经过一会儿达到一个恒定的速度v1,这时加上电场强度为E的匀强电场,再过一会儿达到另一恒定速度v2.在这样短的时间内速度变为恒定,说明油滴受到 的作用,这个力的大小与速度成正比,可表示为kv(式中k为常量)而方向与 .设油滴质量为m,电量为q,写出这两种情况下的方程式① ;② .
|
|
| 图10 |
下面的表是通过这样的实验所测得的不同油滴所带电量q值的一个实例:q的测定值(单位:10-19C)
| 6.41 | 8.01 | 9.65 | 11.23 | 11.83 | 14.48 |
分析这些数据可知:
(答案.空气阻力 速度方向相反 ①mg-kv1=0 ②mg-kv2-qE=0 小球的电量是1.6×10-19C的整数倍,故电荷的最小电量为1.6×10-19C)
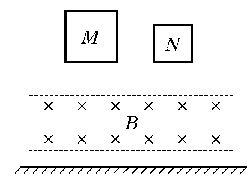
例14.用长度相同,横截面积之比为2∶1的均匀铜导线制成的两个正方形线框M和N,使它们从同一高度自由下落,途中经过一个有边界的匀强磁场区域,磁场方向垂直纸面向里,如图11所示.若下落过程中线框平面始终与磁场方向保持垂直,不计空气阻力,则M、N底边进入磁场瞬间的速度vM∶vN= ,加速度aM∶aN= ,在穿过磁场的过程中,线框M、N内产生的热量QM∶QN= .
(答案:1:1,1:1,2:1)
|
|
| 图11 |
例15.现有一电阻箱,一个开关,若干根导线和一个电流表,该电流表表面上有刻度但无刻度值,要求设计一个能测定某电源内阻的实验方案(已知电流表内阻可忽略,电流表量程符合要求,电源内阻约为几欧).
要求:①画出实验电路图;
②简要写出完成接线后的实验步骤;
③写出用测得的量计算电源内阻的表达式r= .
答案:(1)图略 (2)①使电阻箱阻值最大,合上开关S,调节电阻箱阻值为R1,记下电流表对应的刻度N1;②调节电阻箱阻值为R2,记下电流表对应的刻度N2;③计算出r的值;④多侧几次;取r的平均值;⑤断开S,拆除电阻,整理器材.(3)(N1R1-N2R2)/(N2-N1)
例16.有一质量为M的气缸,平放在光滑的水平面上静止不动,质量为m的活塞把一定质量的理想气体封闭在气缸中,气柱长为L,活塞被销子固定,如图12所示.已知大气压为p0,封闭气体的压强为2p0,拔掉销子,活塞能达到的最大速度为v1,若这一过程中气体的温度不变,活塞与气缸之间摩擦不计,求活塞达到最大速度时:
|
|
| 图12 |
气缸的速度v2;
气柱的长度L1;
气缸移动的距离S及这一过程中气体吸收的热量Q.
解 (1)mv1=Mv2,∴v2=(m/M)v1.
(2)活塞达最大速度,a=0,故p=p0,由玻马定律
| 2p0Ls′=pLs′,L′=2L. |
(3)m=(L-s)/t=M(s/t),s=(mL/M+m),
Q=(1/2)Mv12+(1/2)mv22=[(M+m)mv12/2M]
例17.如图13所示为一固定在水平面上长L的绝缘板,整个空间有一水平的匀强电场,板在右半部有一个垂直于纸面向外的匀强磁场.一质量为m、带电量为q的物体,从板的P端由静止开始在电场力的作用下向右运动.小物体与水平面间摩擦系数为μ,进入磁场区域后恰能作匀速运动.当物体碰到挡板Q后被弹回.若在碰撞瞬间撤去电场,物体返回时在磁中仍能作匀速运动,离开磁场后作匀减速运动,并停在C点.设PC=1/4L.求:
|
|
| 图13 |
物体与挡板碰撞前后的速率v1和v2;
磁感应强度B的大小;
(3)电场强度E的大小和方向.
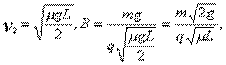
解 物体从P静止开始运动进入磁场速度v1,由动能定理得
| qE(L/2)-μmg(L/2)=(1/2)mv12, |
进入磁场匀速,由反弹后仍匀速可知,电荷带正电.电场强度方向水平向右;进入磁场匀速
| qE=μ(mg+qv1B), |
反弹后匀速
| mg=qv2B, |
出磁场后到C点停止
| -μmg(L/4)=-(1/2)mv22; |
![]()
![]()
![]()
![]() ,方向水平向右.
,方向水平向右.
例18.如图14所示,A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M=2.0kg,
|
|
| 图14 |
长度皆为L=1.0m.C是质量为m=1.0kg的小物块.现给它一初速度v0=2.0m/s,使它从板B的左端向右滑动.已知地面是光滑的,而C与板A、B之间的动摩擦因数皆为μ=0.10.求最后A、B、C各以多大的速度做匀速运动.取重力加速度g=10m/s2.
参考解答 先假设小物块C在木板B上移动x距离后,停在B上.这时A、B、C三者的速度相等,设为v,由动量守恒得
mv0=(m+2M)v, ①
在此过程中,木板B的位移为s,小物块C的位移为s+x.由功能关系得
-μmg(s+x)=(1/2)mv2-(1/2)mv02,
μmgs=2Mv2/2,
则 -μmgx=(1/2)(m+2M)v2-(1/2)mv02,②
由①、②式,得
x=[mv02/(2M+m)μg], ③
代入数值得 x=1.6m. ④
x比B板的长度大.这说明小物块C不会停在B板上,而要滑到A板上.设C刚滑到A板上的速度为v1,此时A、B板的速度为v2,则由动量守恒得
mv0=mv1+2Mv2, ⑤
由功能关系,得
(1/2)mv02-(1/2)mv12-2×(1/2)mv22=μmgL,
以题给数据代入,得
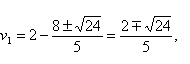
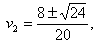
由v1必是正值,故合理的解是
![]()
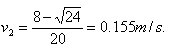
当滑到A之后,B即以v2=0.155m/s做匀速运动,而C是以v1=1.38m/s的初速在A上向右运动.设在A上移动了y距离后停止在A上,此时C和A的速度为v3,由动量守恒得
Mv2+mv1=(m+M)v3,
解得 v3=0.563m/s.
由功能关系得
(1/2)mv12+(1/2)mv22-(1/2)(m+M)v32=μmgy,
解得 y=0.50m.
y比A板的长度小,所以小物块C确实是停在A板上.最后A、B、C的速度分别为vA=v3=0.563m/s,vB=v2=0.155m/s,vC=vA=0.563m/s.
评分标准 本题的题型是常见的碰撞类型,考查的知识点涉及动量守恒定律与动能关系或动力学和运动学等重点知识的综合,能较好地考查学生对这些重点知识的掌握和灵活运动的熟练程度.题给数据的设置不够合理,使运算较复杂,影响了学生的得分.从评分标准中可以看出,论证占的分值超过本题分值的50%,足见对论证的重视.而大部分学生在解题时恰恰不注重这一点,平时解题时不规范,运算能力差等,都是本题失分的主要原因.
解法探析 本题参考答案中的解法较复杂,特别是论证部分,①、②两式之间的两个方程可以省略.下面给出两种较为简捷的论证和解题方法.
解法一 从动量守恒与功能关系直接论证求解.设C刚滑到A板上的速度为v1,此时A、B板的速度为v2,则由动量守恒,得
mv0=mv1+2Mv2,
以系统为对象,由功能关系,得
(1/2)mv02-(1/2)mv12-2×(1/2)mv22=μmgL,
由于v1只能取正值,以题给数据代入得到合理的解为
![]()
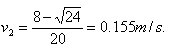
由于小物块C的速度v1大于A、B板的速度v2,这说明小物块C不会停在B板上.
以上过程既是解题的必要部分,又作了论证,比参考答案中的解法简捷.后面部分与参考答案相同,不再缀述.
解法二 从相对运动论证,用动量守恒与功能关系求解.
以地面为参照系,小物块C在A、B上运动的加速度为aC=μg=1m/s2,A、B整体的加速度为aAB=μmg/2M=0.25m/s2,C相对A、B的加速度a=aC+aAB=1.25m/s2.假设A、B一体运动,以A、B整体为参照物,当C滑至与整体相对静止时,根据运动学公式,有
v02=2as,
解得 s=v02/2a=1.6m>L.
说明小物块C不会停在B板上.
上述可以看出,从相对运动的角度论证较为简捷,运算也较为简单.论证后的解法与参考答案相同.
试题拓展 1.若长木板个数不变,当小物块的初速度满足什么条件时,A、B、C三物体最终的速度相同?
2.若长木板个数不变,当小物块的初速度满足什么条件时,小物块能从两长木板上滑过去?
3.若小物块的初速度不变,将相同的长木板数增加到三个,最终小物块停在木板上的什么位置,各物体的运动速度分别为多少?
4.若其它条件不变,长木板与地面间的动摩擦因数为μ′,并且满足μ′(M+m)g<μmg<μ′(2M+m)g,试分析有怎样的情况发生?
5.分析子弹打击在光滑水平面上的两相同木块问题,找出它与本题的异同,归纳解法.