有关粒子在磁场中运动类问题的预测
缙云中学 刘元祥
高考回顾和预测
粒子在单一磁场中的偏转问题的题目近几年高考考查的重点,在96年、99年、2000年、2001年的全国高考试题中皆以计算题的形式考查。但在全国高考理综试题中只在2002年出现(电视机偏转问题)而且题目较为简单,2003年没有考查,做为高考热点和主干知识在2004年高考中出现的几率很大。
在历年高考中粒子在单一磁场中的偏转问题以轨迹考查为主,如多个半圆或1/4圆的组合。其中粒子在交变磁场中运动并不多见,如果是磁场是变化的,运动就更为复杂,一般都存在多值情况。能很好的考查学生思维的多元性和空间的想象力,这类问题有可能成为今年高考的热点。下面通过对一组相关精选习题的分析,(尤其是变形1)探讨此类问题的求解方法,相信会对考生今年的备考大有裨益。
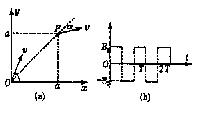
例题:如图(![]() )所示x≥0的区域有如图(b)所示大小不变、方向随时间周期性变化的磁场,磁场方向垂直纸面向外时为正方向,现有一质量为m,带电量为q的正电粒子,在t=0时刻从坐标原点O以速度v沿着与x轴正方向成750射入。粒子运动一段时间到达P点,P点坐标为(
)所示x≥0的区域有如图(b)所示大小不变、方向随时间周期性变化的磁场,磁场方向垂直纸面向外时为正方向,现有一质量为m,带电量为q的正电粒子,在t=0时刻从坐标原点O以速度v沿着与x轴正方向成750射入。粒子运动一段时间到达P点,P点坐标为(![]() .
.![]() ),此时粒子速度方向与OP延长线的夹角为300,粒子在这过程中只受磁场力作用。
),此时粒子速度方向与OP延长线的夹角为300,粒子在这过程中只受磁场力作用。
(1)若B0=B1为已知量,试求粒子在磁场中运动时轨道半径R及周期![]() 的表达式
的表达式
(2)说明在OP间运动时时间跟所加磁场的变化周期T之间应有什么样的关系才能使粒子完成上述运动。
(3)若B0为未知量,那么所加磁场的变化周期T、磁感应强度B0的大小各应满足什么样的条件,才能使粒子完成上述运动?(写出T及B0各应满足的条件表达示)
 解析:(1)由
解析:(1)由
![]()
![]()
![]() 又
又![]()
![]()
![]()
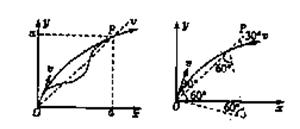 (2)根据粒子经过O点与P点时的速度方向以及B0的方向可以知道:由O至P的运动过程可能在磁场变化的半个周期完成;
(2)根据粒子经过O点与P点时的速度方向以及B0的方向可以知道:由O至P的运动过程可能在磁场变化的半个周期完成;
当磁场方向改变时,粒子绕行方向也变化,由于磁场方向变化的周期性,因此粒子绕行方向也具有周期性,由此可知;由O至P的运动过程也可能在磁场变化半周期的奇数倍时完成。
(3)若粒子在磁场变化的半个周期恰好转过![]() 圆周,同时OP间运动时间是磁场变化半周期的奇数倍时,可使粒子到达P点并且速度满足题设要求。应满足的时间条件:
圆周,同时OP间运动时间是磁场变化半周期的奇数倍时,可使粒子到达P点并且速度满足题设要求。应满足的时间条件:
![]()
![]()
在磁场变化的半个周内粒子的偏转解为600(如图)所以,在磁场变化的半个周期内,粒子在OP方向上的位移也等于R。粒子到达P点而且速度符合要求的空间条件是:
![]()
![]()
![]()
![]()
代入T的表达式的:![]()
延伸与拓展:如果题目图示中未标出速度在OP延长线下方,题干中只要求速度方向与OP延长线夹角为300,还存在另外一种多值情况。
简答如下:
此时仍有![]()
![]() 成立
成立
由几何关系可得OP是R的整数倍
![]()
![]()
代入T表达式上式可得:![]()
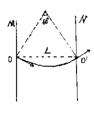
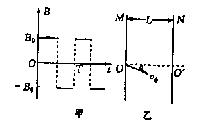 变形训练1(高考打靶):如图所示,平行金属板M,N竖直放置,相距L,在水平轴线上与板的交点O、O/开着两个小孔,两板之间分布着变化的匀强磁场B,B随时间的变化如图甲所示,B随时间的变化如图甲所示,B的正方向垂直纸面向里,在t=0时刻,一个质量为m带正电q的粒子从O点以v0速度入射,v0与OO’夹角
变形训练1(高考打靶):如图所示,平行金属板M,N竖直放置,相距L,在水平轴线上与板的交点O、O/开着两个小孔,两板之间分布着变化的匀强磁场B,B随时间的变化如图甲所示,B随时间的变化如图甲所示,B的正方向垂直纸面向里,在t=0时刻,一个质量为m带正电q的粒子从O点以v0速度入射,v0与OO’夹角![]() =300,已知B的变化周期为T,设带电粒子的速率保持不变(B与v0均未知),为使粒子从O/点出射,求B、v0的值。
=300,已知B的变化周期为T,设带电粒子的速率保持不变(B与v0均未知),为使粒子从O/点出射,求B、v0的值。
解析:最简单的情况是粒子运动![]() 时间内完成上述圆周运动
时间内完成上述圆周运动
即![]() 可得
可得![]()
 由几何关系易知:
由几何关系易知:![]() 即
即 ![]()
将值![]() 代入得
代入得![]()
由圆周运动的周期性和对称性可知存在多值情况:
可能在![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() 时间内完成上述圆周运动
时间内完成上述圆周运动
此时仍有![]()
![]()
粒子从O’出射,由几何关系易知![]()
将值![]() 代入得可得
代入得可得![]() )
)
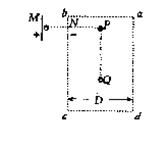 变形训练2:如图所示,一个初速度为零的带正电的粒子经过MN两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd区域内出现大小不变、方向垂直于纸面且方向交替变化的匀强磁场,磁感应强度B=0.4T。每经过
变形训练2:如图所示,一个初速度为零的带正电的粒子经过MN两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd区域内出现大小不变、方向垂直于纸面且方向交替变化的匀强磁场,磁感应强度B=0.4T。每经过![]() s,磁场方向变化一次,粒子到达P点时出现的磁场方向指向纸外,在Q处有一静止的中性粒子,PQ间距离s=3.0m,PQ直线垂直平分ab、cd。已知D=1.6m,带电粒子的荷质比为1.0×104 C/kg,不计重力
s,磁场方向变化一次,粒子到达P点时出现的磁场方向指向纸外,在Q处有一静止的中性粒子,PQ间距离s=3.0m,PQ直线垂直平分ab、cd。已知D=1.6m,带电粒子的荷质比为1.0×104 C/kg,不计重力
求:(1)加速电压为200V时带电粒子能否与中性粒子碰撞?
(2)画出它的轨迹;
(3)能使带电粒子与中粒子碰撞时,加速电压的最大值为多大?
解析:设带电粒子在磁场中运动的半径为r,周期为T,
![]()
![]()
即磁场改变一次方向,粒子正好运动半个周期,
![]()
![]()
得![]() m
m
由于![]() ,带电粒子能与中性粒子相碰
,带电粒子能与中性粒子相碰![]()
 (2)轨迹如图
(2)轨迹如图
(3)要使它们相撞,必须![]()
![]()
显然,当![]() 时,r最大且符合
时,r最大且符合 ![]() 式,即
式,即![]() m
m
代入u表达式得:![]() V
V
总结:通过以上几题我们不难看出,带电粒子在交变磁场中往往是一段圆弧,或多个相同的圆弧,几何分析是突破物体运动图景的关键,通过几何分析找到相关时间和距离的关系。从最基本的运动形式入手,推广到多值的情况。这种熟练应用数学知识的能力也是同学们在平时复习中应重点培养的。