北 京 四 中
年 级：高 三 科 目：物 理 期 数：0119
编 稿： 审 稿： 录 入：张艳红
校 对：刘红梅
高三物理试卷
一、本题共10个小题。每题4分，共40分，每小题给出四个选项，有的小题只有一个选项正确，有的小题多个选项正确。全部选对得4分，选对但不全得2分，错选或不答得零分。
1、一个平行板电容器，充电后与电源断开，当两板间的距离增大时，
A、两板的电势差减小。
B、两板间的电场强度不变。
C、平行板电容器所带的电量不变。
D、平行板电容器的电容减小。
2、如图轻弹簧的一端固定在天花板上，另一端栓一个小球，当小球静止时，弹簧的长度为L1。若对小球施加一个水平力的作用，使得小球再次静止时，弹簧与竖直方向的夹角为60°，
此时弹簧的长度为L2。比较L1和L2，有
A、L1=L2 B、L1<L2 C、L1>L2 D、无法比较.
3、如图所示为某电场中的一条电场线，沿电场线方向有M、N两点。下列说法中正确的是
A、正点电荷在M点的电势能比在N点的电势能大。
B、正点电荷在M点受到的电场力比在N点受到的电场力大。
C、M点的电势比N点的电势高。
D、将正、负电子分别从M点移到N点，电场力对它们做的功相同。
4、将一个秒摆（T=2s）由地球表面移到某一星球表面，其周期变为4s，由此可知
A、该星球半径为地球半径的2倍。
B、该星球半径为地球半径的4倍。
C、该星球表面的重力加速度与地球表面的重力加速度之比为1：4。
D、该星球表面的重力加速度与地球表面的重力加速度之比为1：2。
5、卫星在半径为r的轨道上做匀速圆周运动。它的周期为T，动能为Ek，机械能为E，用某种方法使它的速度突然增大。当它重新稳定下来做匀速圆周运动时，它的
A、r增大，T增大。 B、r增大，T减小。
C、Ek增大，E增大。 D、Ek减小，E增大。
6、如图所示为LC振荡电路中电容器两极板间的电压变化曲线，
由此可知
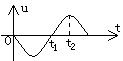A、t1时刻电场能量大，磁场能为零。
B、t1时刻电场能为零，磁场能最大。
C、t1时刻回路中电流为零。
D、t2时刻两极板上的带电量达到最大。
7、边长为L的正方形金属线框a b c d，从某一高度自由下落。它的正下方有高度为h的有界匀强磁场。h>L。线框刚进入磁场时恰好匀速。比较“从ab边进入磁场到线框完全进入磁场”和“从ab边离开磁场到线框完全离开磁场”这两个过程，
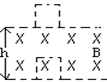A、线框中电流方向相反。
B、线框所受的安培力方向相反。
C、线框中产生的电能相等。
D、线框中产生的电能不相等。
8、如图一列横波向左传播。某一时刻，A、B两质点都处于平衡位置。AB相距为s。AB之间仅有一个波峰。经过时间t，A质点恰好到达波峰位置。则这列波的波速可能是
A、
B、
C、
D、
9、单匝闭合线框在匀强磁场中，绕垂直于磁场方向的转轴匀速转动。在转动的过程中，线框中的最大磁通量为Fm，最大感应电动势为Em。下列说法中正确的是
A、当穿过线框的磁通量为零时，线框中感应电动势也为零。
B、当穿过线框的磁通量减小时，线框中感应电动势在增大。
C、当穿过线框的磁通量等于0.5Fm时，线框中感应电动势为0.5Em。
D、线框转动的角速度等于
。
10、如图所示，物体A放在粗糙的固定斜面上。它沿斜面下滑时加速度为a1。若在A上再放一个物体B，让它们保持相对静止一起沿斜面下滑时，加速度为a2，若取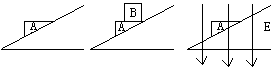
走B，并使A带上正电，处于方向竖直向下的匀强电场中，受的电场力大小正好等于B的重力。此时A下滑的加速度为a3。比较a1、a2、a3，下列关系式正确的是
A、a1=a2 B、a1<a2 C、a3=a2 D、a3>a2
二、本题有7个小题，每小题5分，共35分，把答案填在题中横线上。
11、理想变压器的原、副线圈的匝数分别为n1、n2。初级线圈接正弦交流电，电压有效值为U，次级负载电阻的阻值为R。则变压器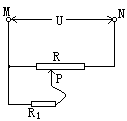
的输入功率为P=____________.
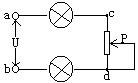
12、如图所示电路中，M、N接恒定的电压U=12V，滑动变阻器总电阻为R，负载电阻R1两端电压的取值范围是____________.若R1=R，当滑键P处于变阻器的中点时，R1两端的电压是____________.
13、如图劈形物块固定在水平地面上。它的高为2m，倾角为30°，物体A质量为5kg，它从斜面顶端以2m/s的速度匀速滑到底端。若取g=10m/s2，在这个过程中，劈形物块对A的作用力的冲量大小为____________，方向为_______________。
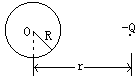14、半径为R的均匀导体球，放在一个负点电荷的电场中。点电荷的电量为Q，与球心O的距离为r。则球体中感应电荷在O点处产生的场强大小为____________，方向为______________________。
15、如图所示电路，ab端接电源，当滑动变阻器的滑片P上下移动时，电路中的两个灯泡都不亮，用电压表检测电路，测得Uab=U，Ucd=U，Uac=0,Ubd=0。
则故障的原因可能是_________________________________。
16、载人飞船的起飞阶段，宇航员的血液处于超重状态，严重时会发生黑视。为使宇航员适应这种情况，要进行训练。宇航员座舱在竖直面内做匀速圆周运动。圆周半径R=20m，座舱向心加速度a=60m/s2。那么座舱每分钟转过的圈数为_________________。飞船起飞时，宇航员躺在水平躺椅上，飞船向上的加速度为60m/s2。宇航员质量为70kg。此时宇航员对躺椅的压力大小是______________。
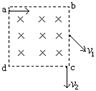17、在正方形a b c d范围内，有垂直于纸面向里的匀强磁场。电子束从a沿a b方向进入磁场。其中速率为v1的电子从bc的中点射出磁场。速率为v2的电子从c沿bc方向射出磁场。
则v1：v2=______________。
三、本题有6个小题，共75分。解答应有必要的草图、文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算，答案中必须明确写出数值和单位。
18、（11分）求证：做匀变速直线运动的物体，在连续的相同时间间隔的位移之差，等于一个常量。
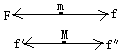
19、（12分）如图所示，木板长为L，质量为M，它静止在水平地面上，与地面间的动摩擦因数为m，质量为m的小木板静止在木板的最右端。现在用水平恒力F向左拉动小木块，经过时间t，小木块到达木板的最左端，在此过程中，木板一直静止，木块与木板间存在摩擦，求此过程中，地面对木板的摩擦力。
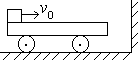20、（12分）如图所示，质量m=2kg的平板小车的左端放有质量M=3kg的铁块。铁块与车之间的动摩擦因数m=0.5。开始时，它们一起以速度v0=3m/s向右在光滑的水平面上运动，后来与竖直墙发生时间极短的碰撞，且没有机械能的损失。由于车足够长，铁块总不能和墙相撞。g取10m/s2。
求：（1）从小车与墙第一次碰撞，到铁块与小车第一次相对静止的过程中，铁块在小车上运动的距离。
（2）请你判断小车最后会停在什么位置。
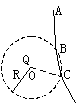21、（13分）如图所示，正点电荷Q固定在O点。在过O点的竖直平面内有一个质量为m，电量为q的质点从A点由静止释放。实线是该质点的运动轨迹。虚线是以O为圆心，以R为半径的圆。轨迹与圆交于B、C两点。已知O、C两点在同一水平线上，且∠COB=30°若该质点在C点的速度大小为v，求它在B点的速度大小。
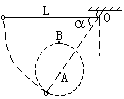22、（13分）长L的轻绳一端固定在O点，另一端栓一个小球。把绳拉成水平伸直，由静止释放小球。绳转过a角时，碰到在A点的固定长钉。小球将以A为圆心继续在竖直平面内做圆周运动。求若要使小球能经过最高点B，OA之间的距离d应满足什么条件。
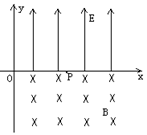
23、（14分）如图所示，在x轴的正上方有匀强电场。电场强度为E，方向沿+y方向。在x轴的下方有匀强磁场，磁感应强度为B，方向垂直于纸面向里。在x轴上有一点P（b，0）（b>0）。在第一象限有一个带电质点，电量为-q，质量为m。质点在某处由静止释放后，能经过P点。不计重力的影响，试讨论释放点的坐标x，y应满足什么关系。（有多种可能）
参考答案
一、选择正确答案。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A BCD | A BCD | ABCD | ABCD | AB C D | A BC D | AB CD | A BCD | A BC D | AB C D |
每小题选对得4分。选不全，该小题得2分。有错选的，该小题得零分。
二、填空题（共35分）
11、
（5分）
12、0至12V（3分）4、8V(2分)
13、100N·s（3分）竖直向上(2分) 14、
（3分）向左（2分）
15、变阻器断路（3分）两灯全短路（2分）
16、16.5（3分） 4900N或4886N（2分）
17、5：4（5分）
三、计算题（75分） 不同解法，只要正确都可相应得分。
18、（11分）作示意图（2分）选时间间隔为T，对应位移
依次为sn，sn+1，sn+2，……。加速度为a。
sn=vAT+
aT2
sn+1=vBT+aT2 （3分）
两式相减sn+1-sn=（vB-vA）T （2分）
而vB-vA=aT （2分）
∴sn+1-sn=aT2 为一个常量 （2分）
19、（12分）木块和木板受力如右图 （1分）
以木块为研究对象 以加速度方向为正
L=at2
（2分）
F-f=ma （2分）
以木板为研究对象f '=-f '' （2分）
根据牛顿第三定律f'=-f （2分）
由各式解得f '=F-
（2分）方向向右（1分）
20、（12分）刚与墙碰撞后，车以原速率反弹，铁块速度方向不变
（1）选v0方向为正，以系统为研究对象：
动量守恒：Mv0+m（-v0）=（M+m）v1 （2分）
功能关系 mMgL=（M+m）v02-（M+m）v12（4分）
解得 共同速度v1=0.6m/s 方向向右 （2分）
铁块在小车上滑动L=1.44m （2分）
（2）小车右端停在墙边 （2分）
21、（13分）研究带电质点从B到C运动的过程：
B、C处于同一等势面上，移动电荷q从B到C，电场力的功
W电=qUBC=0 （3分）
对质点由B到C的过程应用动能定理，只有重力做功
W=mvC2-mvB2 （3分）
W=mg（Rsin30°） （5分）
解得 vB=
（2分）
22、（13）设小圆半径为x，小球在B点速度为v，小球质量为m，受绳拉力为T。
小球在B点：T+mg=m
（2分）
能过B点的条件是T≥0即v≥
……（1） （2分）
设B处为小球势能零点
由机械能守恒mv2=mg[Lsina-x（1+sina）]……（2） （5分）
其中 x=L-d……（3） （2分）
由（1）（2）（3）式解得d≥
（2分）
23、（14分）
（1）当x<b时,由于带电质点进入磁场后,向左偏转,则无论y为何值,均不能到P。 （3分）
（2）当x=b时,由于带电质点在电场中匀加速直线运动,则y取任意值,均可到P。（3分）
（3）当x>b时,设带电质点进入磁场时的速度为v。
由动能定理 qEy=mv2（2分）
进入磁场后 qvB=
（2分）
依题意： x-b=2nr（n=1，2，3……）（2分）
解得 y=
（n=1，2，3……）（2分）