高三物理在解力学题过程中规律的选用
解决动力学问题的方法有三种：一是牛顿定律，二是动量关系，三是能量关系。那么在解题过程中，如何正确选用力学规律呢？下面谈几点看法。
（一）理解规律的适用情况，选取最佳规律。
许多物理习题往往有几种解法，若选用的规律合适，那么解题就非常简单。因而，在解题时不但要强调审清题意，分析物理过程，尽量使已知条件与待求量直接包含在所选规律之中，这就要求不但要熟练掌握规律，而且要透彻理解各规律的适用情况。
①研究某一时刻（或某一位置）的动力学问题应使用牛顿第二定律，研究某一过程的动力学问题，若物体受恒力作用，且又直接涉及物体运动过程中的加速度问题，应采用运动学公式和牛顿第二定律求解。
②对于不涉及物体运动过程中的加速度而涉及运动时间的问题，特别对于打击一类问题，因时间短且冲力随时间变化，则应用动量定理求解。
③对于不涉及物体运动过程中的加速度和时间问题无论是恒力做功还是变力做功，一般都利用动能定理求解。如果物体只有重力和弹力做功而又不涉及运动过程的加速度和时间问题，则采用机械能守恒定律求解。
④对于碰撞、反冲一类的问题，应用动量守恒定律求解。对于相互作用的两物体，若明确两物体相对滑动的距离，应考虑选用能量守恒定律建立方程。
其中要注意：应用动量定理、动能定理、动量守恒定律等规律来解题时，物体的位移和速度都要相对同一个参考系。一般都统一以地球为参考系。
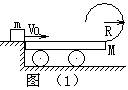【例1】 如图（1）所示，在光滑水平地面上有一质量为M的小车，车上装有一个半径为R的光滑圆环。一个质量为m的小滑块从跟车面等高的平台以初速度V0滑入圆环。试问：小滑块初速度V0满足什么条件时，才能使它运动到圆环最高点时恰好对环顶无压力？
【解析】滑块滑到圆环的最高点恰对环顶无压力时，应有：
……①
式中V是滑块相对圆心O的线速度，方向向左。
设小车此时的速度为V1，并以该速度的方向为正方向，则滑块对地的速度为
，对滑块和小车组成的系统，由于水平方向所受合外力为零，由动量守恒定律得：
……②
由滑块和小车组成的系统机械能守恒得：
……③
由①②③式联立解得：
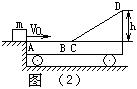【例2】 如图（2）所示，一平板小车静止在光滑的水平地面上，车上固定一倾角为θ，h=0.52米的斜面体，小车与斜面体总质量M=4千克，车上AB面水平、粗糙，长为3.6米，BC是与CD、AB都相切的一小段圆弧面，圆弧BC长可忽略，BCD是光滑的。现有质量m=1千克，长度可不计的小滑块以水平初速度V0滑上小车，若V0=5米/秒，则滑块接触小车后经过1秒钟在AB上的某处相对小车静止。求：
①滑块与小车的动摩擦因数；
②要使滑块滑上小车后不从D处飞出，V0应在什么范围？（g取10米/秒2）
【解析】（1）滑块滑上小车后，滑块与小车组成的系统水平方向不受外力，系统水平方向动量守恒。1秒钟后滑块相对小车静止，说明两者获得了共同速度。选该过程对系统运用动量守恒定律得：
，
再选滑块为研究对象，由动量定理得：
，
两式联立解得：
（2）若要滑块滑上小车后不从D处飞出，则其临界状态为：滑块滑到D点时，与小车获得共同速度，因为系统水平方向动量守恒，则有：
由系统的能量关系可得：
≤
联立解得：
≤7米/秒。
（二）注意过程的整体分析，灵活选用规律
对涉及有多个物理过程的习题，对其物理过程进行整体分析，从而灵活选用物理规律直接用于整体过程，将会使解题步骤大为简化。
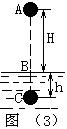
【例3】一钢球从沙坑上方H=5米高处落下，撞入沙中深h=8厘米。假设空气阻力是球重的0.04倍求沙的阻力与钢球重力之比。
【解析】如图（3）所示，选钢球开始下落时（A位置）为初状态，初速度V0=0；钢球停止运动时（C位置）为末状态，末速度Vt=0，触沙前钢球受重力G和空气阻力0.04G，触沙后钢球受重力G和沙的阻力f，对整个过程运用动能定理有：
则可得：
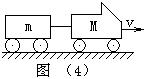
【例4】如图（4）所示，质量为M的汽车，拉着质量为m的拖车，以速度V在平直的道路上匀速前进。后因挂钩脱开，拖车离开汽车，并最后停下来。若汽车的牵引力始终不变，且摩擦力、阻力与车重成正比，而与速度无关。求拖车停止的时刻，汽车的速度是多少？
【解析】以汽车、拖车组成的系统和拖车停止前的全过程为研究对象。在此过程中，牵引力与摩擦阻力始终不变，且始终平衡，即系统受到的合外力为零；而汽车与拖车之间的相互作用力为系统内力，并不改变系统总动量。
设拖车停止时刻汽车的速度为V/，由动量守恒定律可得：
则可知
这里，由于恰当地选取运动过程，使动量守恒的条件得以满足，若以脱钩前后分段处理，必须采用牛顿运动定律和功能关系求解，步骤就繁琐了。
同时必须指出，整体过程分析应建立在各具体过程分析的基础上，而简捷、新颖的解题方法又是以常规解法作基础的。因此，解题切勿不求其解，一味追求简便方法，以免陷入迷途。
E-mail:
电话：0393-