北 京 四 中
年 级：高 三 科 目：物 理 期 数：0129
编 稿：李建宁 审 稿：李建宁 录 入：张艳红
[本周内容]：高三物理复习气体的性质
[重点]：1、气体的状态和状态参量
2、气体三个实验定律。
3、理想气体状态方程及应用。
[讲解]：
1、气体的状态和状态参量。
（1）气体压强P：它是大量分子频繁碰撞器壁产生的，它的大小与单位体积内的气体分子数和分子平均速率有关。
单位：帕斯卡（Pa）
1Pa=1
单位换算：1atm=1.01×105Pa=76cmHg
（2）气体的体积V：是气体所能达到的空间，即容器的容积。
单位：米3（m3）1m3=103cm3（l）=106cm3（ml）
（3）气体的温度T：是反映系统大量分子无规则热运动的剧烈程度，分子平均动能的标志。
摄氏温标：t单位℃，热力学温标：T单位K T=273+t。
（4）三个参量（一定质量的气体）只有一个参量改变是不可能的，至少两个同时改变。
2、气体实验定律。
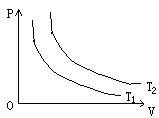（1）等温变化，玻一马定律：一定质量的气体，在温度不变情况下，它的压强跟体积成反比。
P1V1=P2V2=恒量
等温变化过程中理想气体内能不变。 T2>T1
当体积增大时，气体对外做功，吸收热量。
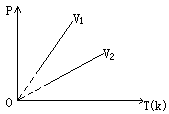（2）等容变化，查理定律：一定质量的气体在体积不变的情况下，它的压强跟热力学温度成正比。或一定质量的气体，在体积不变情况下，温度每升高（或降低）1℃时，所增加（或降低）的压强等于0℃时压强的
。
(V2>V1)
 |
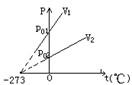Pt=P0（1+
）
等容变化过程气体不做功，吸收或放出的热量等于理想气体内能的增加或减少。
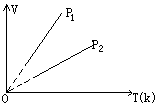（3）等压变化，盖·吕萨克定律：一定质量的气体，在压强不变的情况下，它的体积跟热力学温度成正比。或一定质量的气体，在压强不变的情况下，温度每升高（或降低）1℃时，所增加（或降低）的体积等于在0℃时体积的。
(P1<P2)
 |
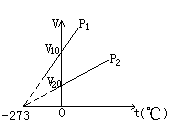Vt=V0（1+）
等压变化过程，当体积增大时，气体对外做功，温度升高内能增加，吸收热量。
3、理想气体的状态方程。
（1）理想气体：能够严格遵守三实验定律的气体。微观上看，分子大小可忽略，分子之间相互作用力可忽略。
（2）表达式：
=恒量
此方程反映一定质量m的理想气体在各个平衡态下，状态参量P、V、T的相互关系，恒量与气体质量，物质的种类有关（与物质的量n有关）
在m不变时，将V=
代入方程（r为气体密度）
可得：
在任意质量的理想气体状态方程——克拉珀龙方程：PV=
RT M为气体摩尔质量，R为摩尔气体恒量
（单位用Pa、m3、k时R=8.31焦/摩开）
此方程反映一定m理想气体在某一平衡态下状态参量P、V、T之间的相互关系。
例题分析：
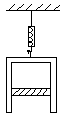1、封有空气的圆型气缸挂在测力计上，测力计的示数为F，已知气缸的质量为M。截面积为S，活塞质量为m，大气压强为P0，活塞与气缸壁摩擦不计，则气缸内气体压强为：
A、P0-
B、P0-
C、P0-
D、P0-
分析：I、研究活塞，画受力图
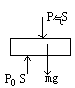SF=0
P气S+mg=P0S
则P气=P0-
故B选项是正确的。
II、研究气缸，画受力图
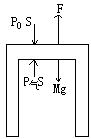SF=0
F+P气S=P0S+Mg
P气=P0+-
又F=（M+m）g代入则
P气=P0+-
=P0-
故B选项是正确的。
2、气缸A和容器B由一细管经阀门K相连，气缸A、B的壁都是透热的，A放在27℃1个标准大气压中，B浸在127℃的恒温槽内。开始阀门k是关断的，B内没有气体，体积VB=2.4升，A装有气体体积 4.8升。打开K使气体由A进入B等活塞停止移动A缸中气体体积VA'=？（活塞与壁摩擦不计，细管容积不计）
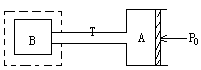分析：方法I：
阀门K打开后气体由A进入B一部分，当活塞不再移动时，A、B中压强不变为PA'=PB'=1atm，B中温度TB=273+127=400k，A中剩余气体V A'仍为300k。
研究B中气体：在原A容器中体积VB'多大？
则VB=1.8升
又VA=VA'+VB' VA'=VA-VB'=4.8-1.8=3L
即气缸A中剩余气体体积为3升。
方法II、
设A气缸中气体质量为mA，剩余质量为mA'，而B缸中气体质量为mB。有：
mA=mA'+mB
根据PV=RT m=
代入上式
已知：PA=PA'=PB=1atm TA=TA'=300k
TB=400k VA=4.8L VB=2.4L
则：
则VA'=3L
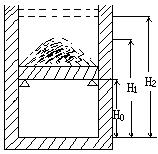
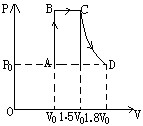3、一个质量可不计的活塞将一定质量的理想气体封闭在上端开口的直立圆筒气缸内，活塞上堆放着铁砂，最初活塞搁置在气缸内壁的固定卡环上，气柱的高度为H0，压强等于大气压强r0，现对气体缓慢加热，当气体温度升高了ΔT=60k时，活塞及铁砂开始离开卡环面上升，继续加热直到气柱高度为H1=1.5H0，此后在保持温度不变的条件下逐渐取走铁砂，直到铁砂全部取走气柱高度变为H2=1.8H0，求此时气体的温度，不计活塞与气缸之间的磨擦。
分析：首先分析气体的状态及状态变化过程，并粗略画出状态变化曲线：
PA=P0
PB=PC
状态A VA=H0S 状态B VB=H0S
TA= TB=TA+ΔT=TA+60K
PC=PB
PD=P0
状态C VC=1.5H0S
状态D VD=1.8H0S
TC=TD TD=TC
A、D两个状态：m不变
即
，
则得TD=1.8TA……（1）
B、C两个状态：m不变
即
则得TD=1.5TA+90……（2）
由（1）和（2）可得TA=300k TD=540k
最后状态D气体的温度为540升。
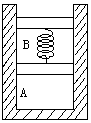
4、如图所示，底面积为20cm2的圆柱形气缸开口向上直立于水平面上，缸内有两个重力均为10N，可沿缸内无摩擦滑动的活塞，封闭着两部分气体，A、B两活塞之间连着一根倔强系数为1000N/m的轻弹簧。当气温为27℃时，两部分气柱长度均等于弹簧的自由长度12cm，当气体的温度升高到多高时，才能使B气柱长度变为16cm？此时气柱A的长度为多少厘米？（已知大气压为1.0×105Pa,气缸足够长,弹簧始终在弹性限度之内。）
分析：当气体温度升高时，B气柱体积将增大，使弹簧处于拉伸状态，B气体压强增大，当温度升至某一数值时弹簧长度变为16cm伸长4厘米。设伸长x=L'-L=16-12=4cm
研究B气柱：对上方活塞进行升温前后的受力分析：
 |
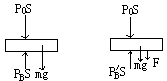（升温前） （升温后）
升温前：PBS=P0S+mg
PB=P0+=1.0×105+
=10.5×104Pa
升温后：PB'S=P0S+mg+F F=kx
PB=P0++=P0++
=1.0×105++
=12.5×104Pa
即初：PB=10.5×104Pa 末：PB'=12.5×104Pa
VB=12×20cm3 VB'=16×20cm3
TB=273+27=300k TB'=？
质量m不变：
代入：
得：TB'=476k
即气体需升至476k，B气柱长度变为16cm，
B气体的体积增大，弹簧的伸长是否影响A气体的压强变化？
将上、下活塞及B气体整体为研究对象可看出，当气体温度增加时，不影响A气柱压强的变化，即A气柱是一个等压膨胀的过程。
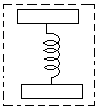
PAS
升温前后相同
PAS
2mg
研究A气柱：
VA=12×20cm3 VA'=L'×20cm3
TA=273+27=300k TA'=476k
M不变，P不变：
VA'=
·VA
L'×20=
×12×20 L'=19cm