子弹射木块问题中的物理规律及其应用

教学目标

引导学生分析并总结子弹射木块中的物理规律，以便于触类旁通处理类似的问题。

教学过程

子弹射木块类问题是一个常见的并且典型的问题，它涉及的物理规律比较广泛，今天这一节课我们要讨论的就是子弹射木块问题中的物理规律及其应用”

放投影：

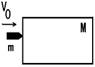
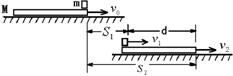
设一质量为M的木块放在光滑的水平面上，另一质量为m的子弹以速度水平射进木块内（如图所示）。假设子弹进入木块深度为d时，子弹与木块具有共同速度，此时木块位移为，子弹位移为，假设子弹所受木块阻力f恒定不变。则在该过程中，子弹、木块或系统可能遵循哪些物理规律呢？请写出相应的表达式。（设取向右方向为正方向）

讨论画什么样的子弹射木块的运动示意图比较好。

讨论总结以下内容：

1、几何关系：

2、对系统应用动量守恒定律：

3、用动量定理：

对子弹：

对木块：

4、用动能定理：

对子弹：

对木块：

5、对系统应用能量转化和守恒定律:

6、应用牛顿第二定律：对子弹:；

对木块：

7、应用匀变速运动公式：

对子弹：作匀减运动，，…

对木块：作匀加速运动，，…

思考题：

1、通常情况下，可不可以认为=0，=0，为什么？

（由于子弹射木块时间极短，如果题目不要求考虑木块的长度，则可认为子弹和木块的位移均为0，射过之后，可认为子弹和木块仍在原来的位置。）

2、如果平面不光滑，木块受摩擦力作用，这种情况还可以认为系统动量守恒吗？

（外力虽不为0，但只要外力远小于内力，可以为动量是守恒。）

3、假设木块厚度为L，子弹射穿木块的条件是什么？

①假设木块足够长，子弹与木块最终速度相同，子弹射穿木块的条件是子弹与木块速度相等时，d≥L；

或：

②假设子弹能够到达木块另一端，子弹射穿木块的条件是d=L时，子弹速度≥木块速度。

小结：

解子弹射穿木块的方法：

1、对子弹射木块问题可从七个方面进行分析；

2、子弹能够射出木块或物块能从木板上滑出的条件可从两方面考虑：

①假设木块足够长，子弹与木块最终速度相同，子弹射穿木块的条件是子弹与木块速度相等时，d≥L；

②假设子弹能够到达木块另一端，子弹射穿木块的条件是d=L时，子弹速度≥木块速度。

3、由于子弹射木块时间极短，如果题目不要求考虑木块的长度，则可认为子弹和木块的位移均为0，射过之后，可认为子弹和木块仍在原来的位置；

例　题：

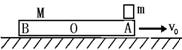
如图所示，质量为M，长为L的木板以速度沿光滑的水平面向右运动，某时刻将一可视为质点的质量为m的铁块轻放到木板的右端。

（1）从两个角度画出运动示意图，并写出相应的铁块从木板左端滑出的条件式；

（2）如果铁块与木板间的滑动摩擦系数为μ，则要使铁块从木板左端滑出，要多大？请写出可能的表达式，并考虑选用哪几个表达式解题比较方便；

（3）如果水平面不光滑，木板与水平面的滑动摩擦系数也为μ，则要使铁块从木板左端滑出，要多大？请写出可能的表达式，并考虑选用哪几个表达式解题比较方便。

分析画出两运动示意图如下：

　　　　

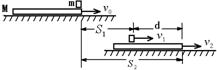
写出相应的滑出条件式：当时，d≥L；或当d=L时，≤。

请两名学生在黑板上分别板书有关问题（2）、（3）的内容（如下），老师巡视学生情况，学生板书结束后，老师作点评 。

解析：（1）

①对系统应用动量守恒定律：

②用动量定理：

对铁块：

对木板：

③用动能定理：

对铁块：

对木板：

④对系统应用能量转化和守恒定律:

⑤应用牛顿第二定律：对铁块:；

　　　　　　　　　　 对木板：

⑥应用运动学知识：

对铁块：作匀减运动，，…

对木板：作匀速运动，，…

⑦几何关系：

⑧滑出的条件：当时，d≥L；或当d=L时，≤。

（2）

①用动量定理：

对铁块：

对木板：

②用动能定理：

对铁块：

对木板：

③对系统应用能量转化和守恒定律:

④应用牛顿第二定律：对铁块:；

　　　　　　　　　　 对木板：

⑤应用运动学知识：

对铁块：作匀减运动，，…

对木板：作匀速运动，，…

⑥几何关系：

⑦滑出的条件：当时，d≥L；或当d=L时，≤。

作业：

子弹射木块类问题练习一：

1、一质量为M的闭合金属螺线管放在光滑水平面上（如图），一条质量为m的条形磁铁以水平速度穿入螺线管并留在其中，求产生的内能为多少。

2、一质量为M的平板在光滑小平面上以速度匀速前进，若在平板前缘轻轻地放上一质量为m的小木块（设它对地初速为零），如图所示，已知木块与木板间的縻擦力恒为f，为使小木块不掉下来，木板的长度最短为多少?

3、如图所示，质量为M，长为L的木板，端点为A、B，中点为O，置于光滑水平面上。现使木板M以的水平初速向右运动；同时把质量为m的长度可忽略的木块置于B端（它对地初速为零），它与木板间摩擦系数为μ。问在什么范围内才能使小木块M滑动到OA之间停下来（即相对木板静止）？

4、在光滑的水平面轨道上有两个半径 都是r的小球A和B质量分别为m和2m，当两球心间距离大于L（L比2r大得多）时，两球心之间无相互作用力，当两球心间的距离等于或小于L时，两球存在相互作用的恒定斥力F，设A球从远离B球处以速度沿两连心线向原来静止的B球运动，如图所示，要使两球不发生接触，必须满足什么条件？

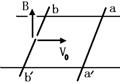
5、如图所示,两根光滑的金属导轨互相平行，处在竖直向上的匀强磁场中。质量为的金属棒aa^/静止在水平导轨上，给质量为的金属棒bb^/一个水平向右的初速度，设运动过程中没有与aa^/相碰，则aa^/能达到的最大速度为多少？

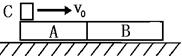
6、如图所示，在光滑水平面上有木块A和B，=0.5kg；=0.4kg，它们的上表面是粗糙的，今有一铁块C，=0.1kg，以初速度=10m/S沿两木块表面滑过，最后停留在B上，此时B、C以共同速度υ=1.5m/s运动，求：（1）A运动的速度υ多大？（2）C刚离开A时的速度υ^/_C多大？

7、在光滑的水平面上，有一质量=20kg的小车，通过一根几乎不可伸长的轻绳与 另一个质量为=20kg的拖车相连接，一质量=16kg的物体放在拖车的平板（足够长）上，物体与平板间的滑动摩擦系数μ=0.20，开始时，拖车静止，绳未拉紧（如图），小车以=3m/s的速度向前运动。求(1) ，，，以同一速度前进时的速度大小。(2)物体在拖车平板上移动的距离，g取10。

8、如图所示，一质量为M，长为L的长方形木板B放在光滑的水平地面上，在其右端放一质量为M的小木快A，m<M， 现以地面为参照系，给A和B以大小相等，方向相反的初速度，使A开始向左运动，B开始向右运动，但最后A刚好没有滑离B板，以地面为参照系，（1）若已知A和B的初速大小为υ，求它们最后的速度大小和方向；（2）若初速度大小末知求小木块A向左运动到达的最远处（从地面上看）离出发点的距离。

9、置于光滑水平面的小车A，B的质量分别为=3kg，=1/2kg，带电量q=C可视为质点的物体C位于光滑小车B的最左端，其质量为=1/10kg，在A，B，C所在的空间有一垂直于纸面（纸面所在平面为竖直平面）向里的匀强磁场，磁感应强度B=10特斯拉，现小车B静止，小车A以速度=10m/s向右运动与小车B碰撞碰后，物体C在小车A上滑动，已知碰后小车B的速度为9m/s，物体C和小车A之间有摩擦，其他摩擦均不计，小车A足够长，求物体C运动的最大速率和小车A运动的最小速度。（g=10）

10、如图所示，质量为2m，长为L的木块置于光滑水平台面上，质量m的子弹以初速度水平向右射向木块，穿出木块时速度为 /2。设木块对子弹的阻力恒定，（1）若木块固定在传送带上，使木块随传送带始终以恒定速度u水平向左运动，子弹仍以初速向右射向木块（u<），求子弹最终速度υ；（2）求在（1）的情况下，子弹在木块中行进的过程中，木块移动的距离S。

11、如图所示，放在光滑水平面上的长木板A的左端叠放着小铁板B，它们一起以=2m/s的速度向右运动。A，B的质量分别为=1kg，=2kg。A与竖直墙壁碰撞后几乎以相同的速度反方向弹回。若A板足够长，在整个运动过程中B没有与墙相碰也不落到地面。A，B间的滑动摩擦系数μ=0.5(g取10)。求：

(1)、与墙第一次碰撞后返回运动过程中，A与墙的最大距离及此时铁块B的速度。

(2)、在整个运动过程中，B相对A所能滑动的最大距离。

(3)、A与墙第一次碰撞后，A运动的总路程。