物理 综合复习(二) 复习中值得关注的几种题型
一、能量的转化问题：
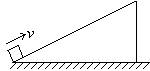
1、小滑块沿固定在水平地面的斜面底端以100J的动能冲上斜面，滑至某一点时，动能减少了80J，重力势能增加了60J，继续上滑一段距离后又返回底端，求返回时的动能。
分析和计算：
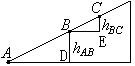
设A到B动能减少了80J，重力势能增加了△EPAB=60J，由此可知这一过程中，滑块克服摩擦力做功WfAB=fSAB=20J，滑块运动到C点速度为0。由右图可知，直角三角形△ABD和△BCE相似，则
。
上式分子和分母分别乘以f和mg有：
。
经B点时滑块还有动能20J，故它从B运动到C的过程中以按1：3的比例转化能量，即增加势能
△EPBC=
EKB=15J，故滑块上升过程中需克服摩擦力做功WfAC=25J，返回A的过程中，滑块受到的摩擦力大小不变，方向沿斜面向上，仍需克服摩擦力做功25J，因此由A到C再返回A的全过程，Wf总=50J，返回A点滑块还有动能50J。
2、如图，光滑的水平地面放置A、B两个木块，mA=3kg，mB=2kg，中间用弹簧相连。A置于墙角，现用力推B，当弹簧具有8J弹性势能时突然撤去外力，将B由静止释放，求：（1）B能达到的最大速度多大？（2）A离开墙壁后，弹簧具有的弹性势能的最大值。
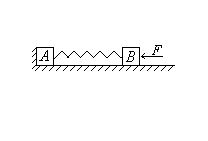
分析和计算：
撤去F后B开始在弹簧弹力作用下加速运动，直到A恰离开墙时速度达到最大，这一过程中，弹簧逐渐恢复原长，弹性势能在A开始运动时全部转化为B的动能。
故有：EP=
mBvB2，所以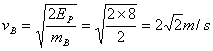
。
A离开墙后，在弹力作用下开始加速，B则减速，这一过程中弹簧不断伸长，直到A、B速度大小相等时，弹簧有最大的伸长，弹性势能达到最大。这是动量守恒的过程。
故有mBvB=(mA+mB)vAB，
此时弹簧的最大弹性势能等于系统动能的减少量，
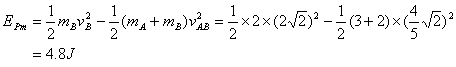
二、电路的分析和计算：
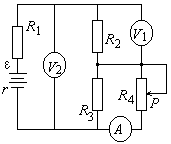
1、如右图所示，当滑动变阻器R4的滑片P向下滑动过程中，电压表v1和v2及电流表A的示数如何变化？
分析：
滑片P向下滑动，滑动变阻器接入电路的电阻减小，因此电路中的总电阻减小，干路电流I1、I2增大，故I2R2增大，V1表的示数增大。电池两端电压U=ε-I1·r，随I1增大U减小，V2表的示数U2=U-I1R1，则U2减小。通过R2流入R3、R4并联电路的总电流I2增大，并联部分的电压U并=U2-I2R2，U并减小，故R3中的电流I3减小。电流表A中示数I4=I2-I3，I4增大。
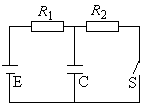
2、如图所示电路，由电阻R1、R2和电容器C组成电路，电池内阻不计，电动势E=10V，R1=4Ω，R2=6Ω，C=30μF，求：
（1）闭合开关S，求稳定后R1中的电流强度。
（2）断开开关S，求这以后通过R1的总电量ΔQ。
分析和计算：
（1）闭合开关S且稳定后电容器极板电量不再变化，电流依次通过R1和R2，则
。
（2）断开S之前，电容器两极板电压UC=IR2=6V，断开S后达到稳定状态，电容器两极板电压等于电源电动势。故在达到稳定状态之前，电源要通过电阻R1向电容器C充电，因此ΔQ=ΔU·C=(10-6)×30×10-6=1.2×10-4C
三、静电场中的几个问题：
1、匀强电场中有a、b、c三点，这三点的电势Ua=16V，Ub=4V，Uc=-2V，画出这三点所在的等势面和电场线的分布情况。
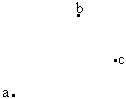
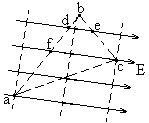
分析及作图：
由题目条件可知Uab=12V，Ubc =6V，故将ab的虚线连接，并将ab四等分，每份长度对应了3V电势差，Ud=7V，Uf=10V，将bc以虚线连接，并将bc平分，则Ue=1V。分别以实线连接de、fc，并做出它们的平行线表示电场线，方向为斜向下，沿电场线是电势降落最快的方向。再分别过a、b、c三点做出电场线的垂线表示等势面。
2、水平向左的匀强电场中，有垂直于纸面向里的匀强磁场，电场强度为E，磁感应强度为B，场中有一固定的竖直放置的绝缘杆，杆上穿过一个质量为m，带有负电q的小球。小球与绝缘杆间的动摩擦因数为μ。若小球由静止下落，且杆足够长，求它沿杆加速滑动达到的最终速度多大？
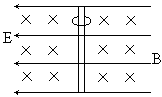
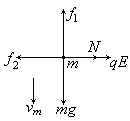
分析和计算：
右图为小球向下运动过程中的受力情况，竖直向下的重力mg，竖直向上的摩擦力f1，水平向右的电场力qE，水平向左的洛仑兹力f2。
这里需要注意的是杆对小球的压力N的大小和方向的变化，当小球速度不太大时，即f2<qE，压力N水平向左，速度不断增大，洛仑兹力不断增大，使得压力N减小，故摩擦力f1在减小，N=0时，f1=0，小球再加速，f2>qE，这时N水平向右，且随速度增大而增大。f1也不断增大。当f1=mg时，小球达到最大速度vm，这时小球开始匀速下落。
由以上分析可知：f1=mg
f1=μN
N=f2-qE
f2=Bqvm
通过以上各式可求得
。