物体平衡问题的求解方法

闫俊仁

（忻州第一中学　 山西　忻州　034000）

物体处于静止或匀速运动状态，称之为平衡状态。平衡状态下的物体是是物理中重要的模型，解平衡问题的基础是对物体进行受力分析。物体的平衡在物理学中有着广泛的应用，在高考中，直接出现或间接出现的概率非常大。本文结合近年来的高考试题探讨物体平衡问题的求解策略。

1．整体法和隔离法

对于连接体的平衡问题，在不涉及物体间相互作用的内力时，应道德考虑整体法，其次再考虑隔离法。有时一道题目的求解要整体法、隔离法交叉运用。

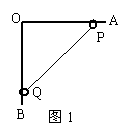[例1]　（1998年上海高考题）有一个直角支架AOB，AO水平放置，表面粗糙，OB竖直向下，表面光滑，AO上套有小环P，OB上套有小环P，两环质量均为m，两环间由一根质量可忽略、不可伸长的细绳相连，并在某一位置平衡，如图1。现将P环向左移一小段距离，两环再次达到平衡，那么将移动后的平衡状态和原来的平衡状态比较，AO杆对P环的支持力N和细绳上的拉力T的变化情况是（　　　　　　　）

A．N不变，T变大　　　　　　　　　　　　　 B．N不变，T变小

C．N变大，T变大　　　　　　　　　　　　　 D．N变大，T变小

解析　用整体法分析，支持力不变。再隔离Q环，设PQ与OB夹角为θ，则不，θ角变小，cosθ变大，从上式看出T将变小。故本题正确选项为B。

2．正交分解法

物体受到3个或3个以上的力作用时，常用正交分解法列平衡方程，形式为，。为简化解题步骤，坐标系的建立应达到尽量少分解力的要求。

[例2]　（1997年全国高考题）如图2所示，重物的质量为m，轻细绳AO与BO的A端、B端是固定的，平衡时AO是水平的，BO与水平面夹角为θ，AO的拉力F₁和BO的拉力F₂的大小是（　　　　　　 ）

A．　　　　　　 B．

C．　　　　　　 D．

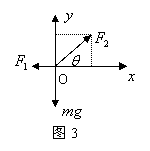
解析　选O点为研究对象，O点受3个力的作用。沿水平方向和竖直方向建立坐标系，如图3所示。由物体的平衡条件；

解得　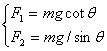 　 　 因此选项BD正确。

3．力的合成法

物体在受到3个共点力的作用下处于平衡状态，则任意2个力的合力必定与第3个力大小相等，方向相反。力的合成法是解决三力平衡的基本方法。

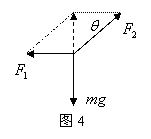
[例3]　上例中，根据三力平衡特点——任意2个力的合力与第3个力等大反向，作出如图4所示和矢量图，由三角形知识可得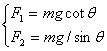　

4．力的三角形法

对受三力作用而平衡的物体，将力平移后，这3个力便组成一个首尾依次相接的封闭的力三角形。力三角形在处理静态平衡和动态平衡问题中时常用到。

[例4]　（1998年广东高考题）如图5细绳AO，BO等长，A点固定不动，在手持B点沿圆弧向C点缓慢运动过程中，绳BO的张力将（　　　　）

A．不断变大　　　　　　　　　　　　　　 B．不断变小

C．先变小再变大　　　　　　　　　　　D．先变大再变小

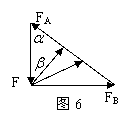
解析　选O点为研究对象，O点受F、F_A、F_B三力作用而平衡。此三力构成一封闭的动态三角形如图6所示。很容易看出，当F_B与F_A垂直时，即时，F_B取最小值。因此，选项C正确。

5．拉密定理法

3个共点力平衡时，每一个力与其所对角的正弦成正比。如图7所示，有（证略）

[例5]　（2003年全国理综高考题）如图8所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的。一根细线跨在碗口上，线的两端分别系有质量为和的小球，当它们处于平衡状态时，质量为的小球与O点的连线与水平面的夹角为。两小球的质量比为（　　　　　　　）

A．　　　　　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

解析　选m₁小球为研究对象，分析受力如图9所示，它受重力G、碗的支持力F_N、线的拉车T（大小等于m₂g）3个共点力作用而平衡。应用拉密定理，有

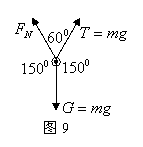所以　　　 　　　　　　故选项A正确。

6．相似三角形法

物理上的矢量可用有向线段表示，矢量的合成与分解又遵守平行四边形法则或三角形法则，这样就构成了一个矢量三角形（平行四边形可分为两个三角形），如果能找到一个由已知量构成的三角形与之相似，那么“相似三角形的对应线段分别成比例”，这一知识就可用于处理物理问题。

[例6]　绳子一端拴着一小球，另一端绕在钉子上，小球放在一光滑的大半球上静止，如图10所示。由于某种原因，小球缓慢地沿球面向下移动，在此过程中，球面的支持力和绳子的拉力如何变化？

解析　本题中小球缓慢移动能看成平衡状态。如图10所示，小球受到3个共点力G、F_N、T作用而处于平衡状态，由G、F_N、T三力组成的力矢量三角形与三角形OAB相似。

设球重为G，大半球半径为R，钉子到球面最高点之距为h，此时绳子长为L，则有　　　　　　

所以　

其中，G、R、h均不变，当L增加时，F_N不变，T增大，所以，本题结论为支持力不变，拉力增大。

7．假设法

假设法解决物体受力平衡问题，常用在判别相互接触物体间的静摩擦力方向。可先假设物体间接触面光滑即不受静摩擦力时，看物体会发生怎样的相对运动，再依据“静摩擦力方向与物体相对运动的趋势方向相反”并结合平衡条件进行判断、求解。

[例7]　（1992年全国高考题）如图11所示，位于斜面上的物块的质量为M，在沿斜面向上的力F作用下，处于静止状态，斜面作用于物块的静摩擦力的（　　　　　 ）

A．方向可能沿斜面向上　　　　　　B．方向可能沿斜面向下

C．大小可能等于零　　　　　　　　　 D．大小可能等于F

解析　除斜面可能作用于物块的静摩擦力f年，物块在沿斜面方向，受到重力的下滑分力和沿斜面方向向上的力F这两个力的作用。

若，则f=0；若，则f≠0且沿斜面向下；若，则f≠0且沿斜面向上，此时有，当时，。

本题的正确选项为A、B、C、D。

8．力矩平衡法

有固定转动轴物体的平衡条件，其合力矩为零，即利用列、解方程。

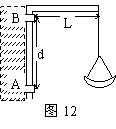[例8]　（2001年津晋理综高考题）图12是轮船上悬挂救生艇的装置的简化示意图。A、B是船舷上的固定箍，以N₁、N₂分别表示固定箍A、B作用于吊杆的水平力的大小，已知救生艇所受的重力G=1500N，d=1m，L=0.8m。如吊杆的质量忽略不计，则（　　　　　　　）

A．N₁=1200N，N₂=0　　　　　　　　　　　　B．N₁=0，N₂=1200N

C．N₁=750N，N₂=750N　　　　　　　　　　D．N₁=1200N，N₂=1200N

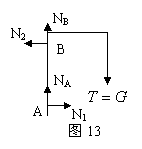解析　隔离吊杆如图13，分析受力有：绳向下的拉力T，箍A对杆的水平作用力N₁和竖直作用力N_A，箍B对杆的水平作用力N₂和竖直作用力N_B。

选B为转动轴，由力矩平衡可得 …………（1）

选A为转动轴，由力矩平衡可得 …………（2）

联立（1）（2）解得 N₁=1200N，N₂=1200N

因此，本题的正确选项为D。

上述处理平衡问题的8种方法，在处理具体问题时各有特点，针对具体总是灵活地选择恰当的方法，会使问题处理变得简捷明子。