高三物理竞赛练习题

　　(例一)如图1所示，两个截面相同的圆柱形容器，右边容器高为H，上端封闭，左边容器上端是一个可以在容器内无摩擦滑动的活塞。两容器由装由阀门的极细管道相连通，容器、活塞和细管都是绝热的。开始时，阀门关闭，左边容器中装有热力学温度为T₀的单原子理想气体，平衡时活塞到容器底的距离为H，右边容器内为真空，现将阀门缓慢打开，活塞便缓慢下降，直至系统达到平衡，求此时左边容器中活塞的高度和缸内气体的温度。

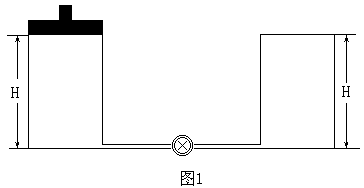
　　提示：一摩尔单原子理想气体的内能为

，其中R为摩尔气体常量，T为气体的热力学温度。

　　(例二)位于竖直平面内的矩形平面导线框abcd，ab长为l₁，是水平的，bc长为l₂，线框的质量为m，电阻为R，其下方有一匀强磁场区域，该区域的上、下边界PP'和'均与ab平行，两边界间的距离为H，H>l₂，磁场的磁感强度为B，方向与线框平面垂直，如图2所示，令线框的dc边从离磁场区域上边界PP'的距离为h处自由下落，已知在线框的dc边进入磁场以后，ab边到达边界PP'之前的某一时刻线框的速度已达到这一阶段的最大值。问从线框开始下落到dc边刚刚到达磁场区域下边界'的过程中，磁场作用于线框的安培力作的总功为多少？

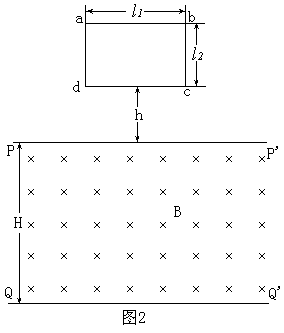
　　例题解答

　　一、设容器的截面积为A，封闭在容器中的气体为v摩尔，阀门打开前，气体的压强为p₀，由理想气体状态方程有

　　p₀AH=vRT₀ (1)

　　打开阀门后，气体通过细管进入右边容器，活塞缓慢向下移动，气体作用于活塞的压强仍为p₀，活塞对气体的压强也是p₀，设达到平衡时活塞的高度为x，气体的温度为T，则有

p₀(H+x)A=vRT

(2)　　根据热力学第一定律，活塞对气体所做的功等于气体内能的增量，即

　　p₀(H－x)A=　　　　　　　　　　　　 vR(T－T₀) (3)

　　由(1)、(2)、(3)式解得　　x＝H　　T＝T₀

二、设线框得dc边刚达到磁场区域上边界PP'时得速度为v₁，则由　　mv₁²=mgh(1)

　　dc边进入磁场后，按题意线框虽然受安培力阻力作用，但依然加速下落，设dc边下落到PP'得距离为△h₁，速度达到最大值，以v₀表示这最大速度，这时线框中得感应电动势为　　ε=Bl₁v₀　　线框中的电流

　　作用于线框的安培力为　　f=Bl₁I= (2)

　　速度达到最大的条件时安培力　　f=mg

　　由此得

　　v₀＝(3)

　　在dc边向下运动距离△h₁的过程中，重力做功A₁=mg△h₁，安培力做功A₂，由动能定理得

　　A₁+A₂=

　　将(1)、(3)式代入得安培力作的功

　　 (4)

　　线框速度达到v₀后，作匀速运动，当dc边匀速向下运动的距离为△h₂=l₂－△h₁时，ab边到达磁场的边界PP'，整个线框进入磁场，在线框的dc边向下移动△h₂的过程中，重力做功A₁^'，安培力做功A₂^'，但线框速度未变化，由动能定理

　　A₁^'+A₂^'=0

　　A₂^'=－A₁^'=－mg△h₂=－mg(l₂－△h₁) (5)

　　整个线框进入磁场后，直至dc边达到磁场区的下边界'，作用于整个线框的安培力为零，安培力作的功也为零，线框只在重力作用下作加速运动。

　　所以，整个过程中安培力作的总功

　　A＝A₂+A₂^'＝－mg(l₂+h)+

　一平凸透镜焦距为f，其平面上镀了银，现在其凸面一侧距它2f处，垂直于主轴放置一

高为H的物，其下端在透镜的主轴上（如图）。

　　1、用作图法画出物经镀银透镜所成的像，并标明该像是虚、是实；

　　2、用计算法求出此像的位置和大小。

　　【例题二】　　一个大容器中装有互不相溶的两种液体，它们的密度分别为ρ₁和ρ₂（ρ₁<ρ₂）。现让一长为L、密度为(ρ₁+ρ₂)／2的均匀木棍，竖直地放在上面液体内，其下端离两液体分界面的距离为3L／4，由静止开始下落。试计算木棍到达最低处所需的时间。假定由于木棍运动而产生的液体阻力可以忽略不计，且两液体都足够深，保证木棍始终都在液体内部运动，既未露出液面，也未与容器相碰。

【例题解答】

　　例题一

　　1、用作图法求得物AP的像A'P'及所用各条光线的光路如图预解所示。　　说明：平凸薄透镜平面上镀银后构成一

个由会聚透镜L和与它密接的平面镜M组合LM。如图预解所示，图中O为L的光心，

AOF'为主轴，F和F'为L的两个焦点，AP为物，作图时利用了下列三条特征光线。　　（1）由P射向O的入射光线，它通过O后方向不变，沿原方向射向平面镜M，然后被M反射，反射光线与主轴的夹角等于入射角，均为α，反射线射入透镜时通过光心O，故由透镜射出时方向与上述反射线相同，即图中OP'。

　　（2）由P发出且通过L左方焦点F的入射光线PFR，它经过L折射后的出射线与主轴平行，垂直射向平面镜M，然后被M反射，反射光线平行于L的主轴，并向左射入L，经L折射后的出射线通过焦点F，即为图中的RFP。

　　（3）由P发出的平行于主轴的入射光线PQ，它经过L折射后的出射线将射向L焦点F'，即沿图中QF'方向射向平面镜，然后被M反射，反射线指向与F'对称的F点，即沿QF方向。此反射线经L折射后的出射线可用下法画出；通过O作平行于QF的辅助线S'OS，S'OS通过光心，其方向保持不变，与焦面相交于T点。由于入射平行光线经透镜后相交于焦面上的同一点，故QF经L折射后的出射线也通过T点，图中的QT即为QF经L折射后的出射光线。

　　上列三条出射光线的交点P'即为LM组合所成的P点的像，对应的A'即A的像点。由图可判明，像A'P'是倒立实像，只要采取此三条光线中的任意两条即可得A'P'，即为正确解答。

　　2、按陆续成像计算物AP经LM组合所成像的位置、大小，物AP经透镜L成的像为第一像，取u₁=2f，由成像公式可得像距v₁=2f，即像在平面镜后距离2f处，像的大小H'与原物相同，H'=H。　　第一像作为物经反射镜M成的像为第二像，第一像在反射镜M后2f处，对M来说是虚物，成实像于M前2f处，像的大小H"也与原物相同，H"=H'=H。　　第二像作为物，再经透镜L而成的像为第三像，这时因为光线由L右方入射，且物（第二像）位于L左方，故为虚物，取物距u₂=-2f，由透镜公式

　　可得像距

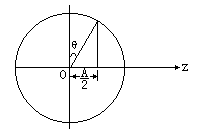
上述结果表明，第三像，即本题所求的像的位置在透镜左方距离2f／3处，像的大小

可由求得，　　像高为物高的

　　例题二

　　1、用S表示木棍的横截面积，从静止开始到其下端到达两液体交界面为止，在这过程中，木棍受向下的重力

和向上的浮力ρ₁LSg。由牛顿第二定律可知，其下落的加速度　　①

　　用t₁表示所需的时间，则　　　　②

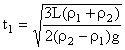　　由此解得 ③

　　2、木棍下端开始进入下面液体后，用L'表示木棍在上面液体中的长度，这时木棍所受重力不变，仍为，但浮力变为ρ₁L'Sg+ρ₂(L-L')Sg。当L=L'时，浮力小于重力；当L'=0时，浮力大于重力，可见有一个合力为零的平衡位置。用L₀'表示在此平衡位置时，木棍在上面液体中的长度，则此时有

　　④　　由此可得 L₀'=L／2 ⑤

　　即木棍的中点处于两液体交界处时，木棍处于平衡状态，取一坐标系，其原点位于交

界面上，竖直方向为z轴，向上为正，则当木棍中点的坐标z=0时，木棍所受合力为零，当中点坐标为z时，所受合力为

　　式中 k=(ρ₂-ρ₁)Sg ⑥

　　这时木棍的运动方程为

　　a_Z为沿z方向的加速度

　　⑦

　　由此可知为简谐振动，其周期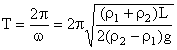⑧

　　为了求同时在两种液体中运动的时间，先求振动的振幅A。木棍下端刚进入下面液体时，其速度　　v=a₁t₁ ⑨

　　由机械能守恒可知⑩　　式中

为此时木棍中心距坐标原点的距离，由①、③、⑨式可求得v，再将v

和⑥式中的k代入⑩式得　　A=L　

　　由此可知，从木棍下端开始进入下面液体到棍中心到达坐标原点所走的距离是振幅的一半，从参考圆（见图）上可知，对应的θ为30⁰，对应的时间为T／12。因此木棍从下端开始进入下面液体到上端进入下面液体所用的时间，即棍中心从

到

所用的时间为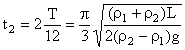　　

　　3、从木棍全部浸入下面液体开始，受力情况的分析和1中类似，只是浮力大于重力，

所以做匀减速运动，加速度的数值与a₁一样，其过程和1中情况相反地对称，所用时间　　t₃=t₁ 　　4、总时间为