高考物理复习：磁场综合面面观(一)
磁场是高考中的一个重点，每年总有大量的分数集中在这个地方，最重要的是，那些相对难度比较大的题，往往出在这里，并且大多数情况下，不会单独出磁场的大题（也没有什么可考的），而往往是磁场与运动学，动力学的结合，磁场与电学的结合，磁场与原子核部分的结合，甚至与化学的结合。很多考生拿不到分数，并不是因为知识点没有掌握好，而是综合能力，也就是各知识点之间融会贯通的能力不足，我们就对磁场与其它知识点的综合题做一个总结。
一． 磁场与运动学动力学的综合
这种题近几年经常出现，在做这种题的时候，一定要按照做运动学动力学做题的过程来研究问题，先进行过程分析，在进行受力分析，再根据上面分析来研究条件结论，来解题。
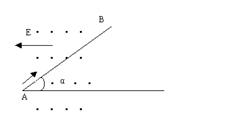例1：如图所示，足够长的绝缘斜面与水平面间的夹角为α（sinα=0.6），放在水平方向的匀强磁场和匀强电场中，电场强度E=50V/m，方向水平向左，磁场方向垂直于纸面向外。一个带电量q = +4.0×10-2C，质量m = 0.40kg的光滑小球，以初速v0 = 20 m/s从斜面底端A冲上斜面，经过3 s离开斜面，求磁场的磁感应强度。（取g =10m/s2）。
1） 运动分析：
有初速度运动滑上去，减速运动某一时刻，该时刻小球离开斜面。
2） 受力分析：
受重力，支持力，磁场力，电场力。
3） 综合分析：
由于小球受到的磁场力必定与它的运动速度方向垂直，由一开始小球在斜面上运动而3s后离开斜面，则可以判定小球初始时受的磁场力的方向为垂直于斜面向下，当然，也可以由左手定则直接判断，也就是说，题中如果不给出小球带的电荷类型，也可以判断出来。
小球沿斜面向下的加速度由电场力F=Eq=2N和重力G=mg=4唯一决定，为 ma=Fsinα+mgcosα=4，所以a =10m/s2，
则3秒小球的速度为v =20-10×3 = -10，方向为沿斜面向下，这时，小球受的磁场力为沿与斜面垂直方向向上，大小为T=qvB。
小球刚好离开斜面意味着此时小球刚好受斜面的弹力为0。于是由沿斜面垂直方向上的受力平衡不难得出T+F sinα = G cosα，
解之即可得B =5T
这个题中，磁场与电场运动学动力学联系到了一起。
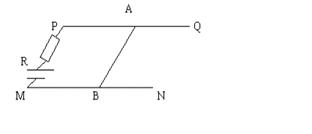例2：如图所示，水平放置的平行的两条光滑金属导轨PQ和MN，放在竖直方向的匀强磁场中。一端和电池、电阻R相连，电池的电动势E = 3.0V，内阻r = 0.50Ω，电阻 R = 3.5Ω。金属棒AB跨接在导轨上，金属棒AB的电阻R1 = 1.0Ω。当金属棒AB的电阻以3.0m/s的速度向右匀速运动时，金属导轨中的电流恰为零。当金属棒AB在水平力F作用下向左匀速运动时，水平力总共的功率是2.0W。求水平力F的大小和方向。
上面我们提到要进行运动分析受力分析，其实就是要同学们做到逢题要先把题完整的分析透，不要盲目下手，一定要把解题过程烂熟于心，方可下手解题，万不可操之过急。
在这个题中，3.0m/s的速度向右匀速运动时，金属导轨中的电流恰为零，所以这时候AB运动产生的电动势应该等于电源电压BLv=E 得到BL=1Vs/m。
当金属棒AB在水平力F作用下向左匀速运动时,设电流为I，受力分析：BIL=F，再根据Fv'=P，而 I=(BLv'-E) /(R+r+R1)
联立可以求出F
这个题用到了磁场，力和电压电流的知识点，是一个多知识点综合的好题。
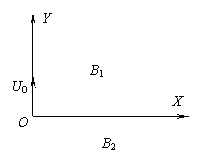例3：地球周围有磁场，由太空射来的带电粒子在此磁场中的运动称为漂移。以下描述的是一种假设的磁漂移运动，一带正电的粒子在x = 0， y = 0处沿y方向一某一速度v0运动，空间存在垂直于图中纸面向外的匀强磁场，在y>0的区域中，磁场强度为B1，在y<0的区域中，磁场强度为B2，B2>B1,如图所示。
（1）把粒子出发点x=0处作为第0次过x轴，试求至第n次过x轴的整个过程中，在x轴方向的平均速度v与v0之比，n只取奇数。
（2）若B2：B1=4，当n很大时，v：v0趋于何值？
无论第几次通过x轴，速度大小都是V0，可以这样解答：
（1） 第一次穿过x轴，沿x轴方向的位移是：S1＝2R1，其中：R1＝mV0/（B1q）
mV0/（B1q），平均速度：V1＝2R1/t1，其中：t1＝T1/2＝πm/（B1q）
第三次穿过，沿x轴方向的路程是：S2＝（4R1－2R2） 取它的绝对值，其中 ：R2＝mV0/（B2q），平均速度：V2＝S2/t2，其中：t2＝T1－T2/2＝2πm/（B1q）－πm/（B2q）
依此类推：
第n次穿过x轴（n取奇数），沿x轴方向的路程是：Sn＝2[nR1－（n－1）R2]
经过时间：tn＝1/2[nT1－（n－1）T2]，速度：V＝Sn/tn
（2） 若B2：B1＝4：1，那么带入上面可得：Vn＝Sn/tn的值，可得这个式子当n趋向无穷大时的极限。
信息给与题是最近几年的热点，平时联系的时候要多加注意。
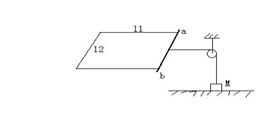例4：金属杆ab放在光滑的水平金属导轨上，与导轨组成闭合举行电路，长l1＝0.8m,宽l2=0.5m,回路总电阻R＝0.2欧姆，回路处在数值方向的匀强磁场中，金属杆用水平绳通过定滑轮连接质量M＝0.04kg的木块，随时间均匀增强，5s末木块将离开水平面，不计一切摩擦，g取10m/s2,求回路中的电流强度。
这道题是典型的动力学与磁场的结合，根据受力分析磁场，再根据磁场还原到力，解题过程如下：
设磁场强度b(t) = b0 + kt，,k是常数，于是回路电动势是e=s△b/△t=ks,s是矩形面积l1× l2，回路电流i=e/r，杆受力f(t) = bi l=(b0+kt)il，5秒末有f(5)=(b0+5t)kl1l22/r=Mg，可以得到k值，于是就可以得到i=ks/r
练习题：如图所示，光滑的水平金属框架固定在方向竖直向下的匀强磁场中，框架左端连接一个R = 0.4Ω的电阻，框架上面置一电阻r = 0.1Ω的金属导体ab，金属导体长为0.5m。两端恰与框架接触，且接触良好。金属导体在F = 0.4N的水平恒力作用下由静止开始向右运动，电阻R上消耗的最大电功率为P = 0.45W。（设水平金属框架足够长，电阻不计。）
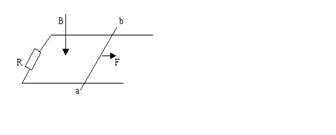1．试判断金属导体a, b两端电势高低。
2．金属导体ab的最大速度。
3．求匀强磁场的磁感应强度。