高考物理复习力学综合专题

————力学方法

　　谈谈如何安排第二轮的物理复习？

  1. 认真学习最新高考说明，对照物理知识点认真学习、思考。思考本知识的内容，知识的应用，知识间的联系。

  2. 对于知识表中自己还没有掌握的知识，特别是在自己头脑的知识库中还没有储存和提取不出来的知识，应该认真学习教材——有针对的复习。

  3. 认真学习过去笔记，这是你在学校学习过程中的宝贵资料。从中提取已经忘却的知识、方法、经验。

  4. 经常翻看已经完成的物理综合练习，看你会的，看你不会的但是经过老师分析试卷后已经会的。如果你的物理学习成绩一般，那么你可以不去花费太多的精力去抠特别的难题。对于物理学习已经达到成熟程度的同学，在巩固基础的条件下，可以看看高能力要求的题目。

  5. 每天一定要安排一定量的练习，要动笔，比如完成四个左右选择题，一个实验题，一到两个计算题。如果你物理成绩一般，可以选择中档题。

  6. 不断总结知识、方法，形成科学知识网络，使能力不断提高。

  7. 在适当的时间，安排理科综合模拟练习——在150分钟内完成。

　　在完成综合试卷的过程中，应该扬长避短，处理好舍和得的关系，——少舍多得，才能够抓住成功的机会。

　　力学知识要点结构网络：

I：力学

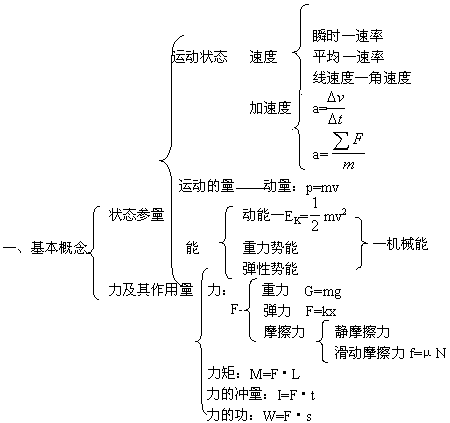
二. 基本规律

  1. 对质点——三条核心规律：

　　·t=mv₂-mv₁(动量定理，矢量式)

　　t↑　　 ↑t

　　=　ma（牛顿运动定律矢量式）　　　　

　　S↓　　 ↓S

　　（动能定理：标量式）

　　万有引力定律：F=G

　　动能定理是标量关系式，功的正负决定能量的具体转化过程，并不表示方向，功和能都是标量。解决复杂运动过程和复杂的力作用过程，动能定理常常是首选的方法。

　　动量定理主要用于解决打击、碰撞、短时间内力变化情况很复杂的过程。动量定理还可以解决在不同时间内受力不同的情况，这时可以不追究作用的细节，只关注初末状态的动量，初末状态的确定依所研究的问题而确定。在实际生活生产中，在物体运动状态的变化一定时，可以用减小作用时间的方法而增加作用力，也可以用延长作用时间的方法而减小作用力。

  2. 对系统——守恒定律：

　　若合外力为零（不受外力），系统动量守恒

　　

　　若只有重力或弹力做功，系统机械能守恒

　　

　　能的转化和守恒定律，能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为别的形式，或者由一个物体转移到别的物体，而在这种转化和转移中保持能的总量不变。

　　通过典型例题分析巩固力学基本方法

【典型例题】

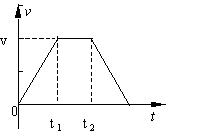
  例1. 在水平地面上有一质量为4kg的物体，物体在水平拉力F的作用下由静止开始运动。10s后拉力减为。该物体的v—t图象如图所示。求：

　　（1）物体受到的水平拉力F的大小。

　　（2）物体与地面间动摩擦因数。（g=10m/s²）

　　类型：已知状态力（μ）

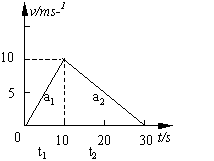
　　解析：方法1，牛顿定律结合运动规律

　　0－10s：F－μmg=ma₁如图：

　　10—30s内：μmg－=ma₂如图：

　　由图像：a₁=　 a₂=

　　联立解得：F＝9N

　　f=5N　　f=μmg

　　μ＝

　　方法2：以动量定理为核心规律：

　　则0—30s：Ft₁+－μmg(t₁+t₂)=0

　　0－10s: Ft₁－μmgt₁=mv_m

　　解得：F＝9N，μ＝

　　方法3：以动能定理为核心规律（能法）

　　由图像信息：

　　

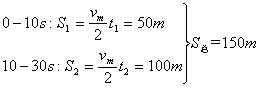
　　0－30s：FS₁+－μmgS_总＝0

　　0－10s：FS₁－μmgS₁=

　　解得：F＝9N，μ＝

　　总结：此外还有许多三种方法结合的解法。

　　对于匀变速运动，三种方法一般均行得通，当直接涉及状态、时间、力时，以动量定理应用最简单。

  例2. 一位同学的家住在一座25层的高楼内，他每天乘电梯上楼，经过多次仔细观察和反复测量，他发现电梯启动后的运动速度符合如图所示的规律，他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度。他将台秤放在电梯内，将重物放在台秤的托盘上，电梯从第一层开始启动，经过不间断的运行，最后停在最高层。在整个过程中，他记录了台秤不同时间段内的示数。记录的数据如下表所示。

　　

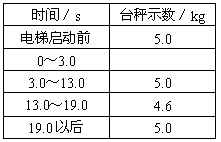
　　但由于0～3.0s段的时间太短，他没来得及将台秤的示数记录下来。假设在每个时间段内台秤示数都是稳定的。重力加速度g取10m/s²。

　　（1）电梯在0～3.0s时间段内台秤的示数应该是多少？

　　（2）根据测量的数据，计算该座楼房每一层的平均高度。

　　解：力法（逆向思维——从“13.0～19.0s”入手）

　　Δt₃=6s，

　　在13.0～19.0s内，如图所示

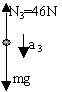
　　mg-N₃=ma₃

　　a₃=

　　a₁=

　　则0～3.0s内，N₁－mg=ma₁（如图）

　　N₁ =ma₁+mg=58N　　m₁=5.8kg

　　0～19.0s内的位移

　　S_总＝

　　其中v=a₁t₁

　　解得：S_总＝69.6m

　　

　　解2：以动量定理为核心规律，则：

　　0～19.0s内（t₁=3s Δt₂=10s Δt₃=6s）

　　N₁t₁+N₂Δt₂＋N₃Δt₃－mgΔt_总＝0

　　（N₂=50N　 t_总＝19s）

　　解得：N₁=58N=5.8千克力

　　在0～t₁内：N₁t₁-mgt₁=mv

　　得：v=4.8m/s

　　S_总为v～t图线下的面积

　　S_总＝m

　　

　　总结：本题同样可由能法处理。

　  请思考：

　  （1）W_G＝？

　  （2）重力势能变化ΔEp=?

　  （3）机械能变化ΔE=?

　  （4）动能变化及总功为多少？

　  （5）总弹力功为多少？

　　应该认识以下结论：

　　（1）重力功及重力势能的变化与路径无关。

　　（2）过程不同，弹力不同，弹力为应变力。

　　（3）过程不同机械能的变化及力的总功等不同。

　　量度ΔE_K的是∑W

　　量度ΔE的是除重力、弹力之外其他力所做的功。

　　涉及相互作用系统问题。

  例3. 在光滑水平面上有质量M＝16kg的长木板A，板上有质量m＝4kg的滑块B。某时刻长木板速度向右、滑块速度向左，且两者的动能都为2J。经过一段时间，长木板和滑块以相同的速度向同一方向运动（滑块仍在长木板上）。求：长木板和滑块共同运动时的速度的大小和方向。

　　涉及相互作用系统应首选“守恒”规律，判断动量或机械能是否守恒。

　　解1：对A、B系统∑F_外＝0，动量守恒

　　依题意：E_KA= E_KB=2J(=E_K)

　　

　　

　　

　　

　　以向右为正，有=(M+m)V

　　（向右）

　　以上注意矢量合成。

　　解2：力法

　　依题意：分别求得v _A=0.5m/s(右)　　v _B=1m/s（左）

　　运动图像如图所示

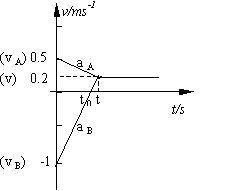
　　　 ①

　　＝　　 ②

　　（注意对应关系）

　　联立可得v

　　展开讨论：

  1. 系统机械能是否守恒？机械能不守恒！

　　转化的内能Q＝？

　　解：

  2. 相互摩擦的长度Δl=?(设μ＝0.5)（g=10m/s²）

　　解：μmgΔl=Q

　　

  3. A至少多长，才能保证B不滑落。

　　（设B从A的右端开始滑起，且不计B的大小）

　　L_min=Δl

　　注意：不是在v _B=0时，就相对静止了，看v—t图，在v _B=0时，v _A>0，此后，B仍相对于A向后滑，在v _B=0时，是相对于地面，B向左滑行的最远点。

  4. 相互滑动的时间有多长？

　　解： 对A：由动量定理

　　μmgt=Mv_A-Mv　（关注M与m的对应）

　　得

  5. 在t内，A的位移有多远？

　　解：对A：由动能定理：

　　

　　

　　问题：B对地的位移？

　　方法总结：应用牛顿运动定律处理问题，把握力与运动的关系

　　

　　

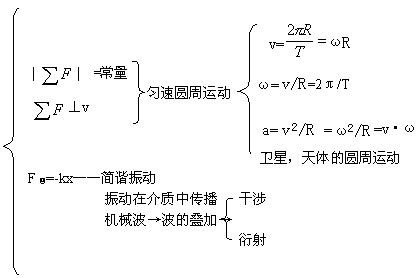
　　应用动能定理解决问题的基本方法：

　1. 明确研究对象，对研究对象做受力分析

　2. 确定物理过程，研究在所确定的物理过程中，哪些力做功，做正功还是负功，求外力对物体做的总功即功的代数和。包括物体受到的所有的力所做的功，包括重力的功，弹力的功。对做功的力的性质没有任何限制，可以是重力、弹力、摩擦力做功，也可以是电场力、磁场力、分子力做功。对力的变化情况没有任何限制，可以是恒力，可以是变力，也可以是不连续的力作用过程。

　3. 确定研究过程的初末状态的动能。

　4. 列动能定理方程，结合其它有关规律分析求解。

　　应用动量定理分析解决问题的基本程序是

　1. 明确研究对象

　2. 确定所研究的物理过程及初、末状态——动量

　3. 分析对象在所研究过程中受力情况——冲量

　4. 规定正方向，列方程分析推理

　　比较力学三个核心定律

　　牛顿定律 ΣF=ma　(矢量式、瞬时式)

　　动量定理 ΣFt=mV-mVo (矢量式、过程式)

　　动能定理 ΣW=mv²/2-mv_o²/2 (标量式、过程式)

　　这是研究质点运动的三条核心规律,它们的意义分别为:力是改变质点运动状态的原因;力在时间上的累积作用——ΣFt量度质点动量的变化;力在空间上的累积作用——W量度质点动能的变化.三条规律为我们解决力学问题提供了三条途径。

　　在研究对象受恒力作用时，三种方法都可以应用；当问题直接涉及状态与空间位移时，用动能定理解决问题来得直接；当问题直接涉及状态和时间时，用动量定理解决问题比较简单；当物体在变力作用下，特别是复杂的曲线运动时，一般首选能法解决问题；当研究对象是一个相互作用的系统时，应首选守恒规律解决。

　　可见，同一问题方法不同，难易程度不同。若涉及状态、空间位移、力，用动能定理更方便。对复杂的变速、曲线运动，能法常常是首选的，有时是唯一的方法。

【模拟试题】

　1. 对运动的合成以下说法正确的是

　　A. 两直线运动的合成一定是直线运动

　　B. 两匀速运动的合成可能是曲线运动

　　C. 两初速度为零的匀变速直线运动的合成一定是直线运动

　　D. 物体受到不在同一方向上的两个力作用一定做曲线运动

  2. 火车在东西方向的水平轨道上行使，已知火车具有向东的恒定加速度，某时刻由火车上的窗口落下一个小球。不计空气阻力，则站在地面上的静止观察者看到小球的运动是

　　A. 只能是向东的平抛运动

　　B. 只能是向西的平抛运动

　　C. 只能是自由落体运动

　　D. 可能是向东可能是向西的平抛运动

  3. 在抗洪抢险中，战士驾驶摩托艇救人。假设江岸是平直的，洪水沿江向下游流去，水流速度为v₁，摩托艇在静水中的航速为v₂，战士救人的地点A离岸边最近处O的距离为d。如战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O点的距离为　

　　A. 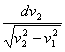　　　　B. 0　　　  C. 　　　　D.

  4. 卫星A、B、C在相隔不远的不同轨道上，以地球为中心做匀速圆周运动，且运动方向相同（A离地球最近，C离地球最远），若在某个时刻恰好与地心在同一直线上，则当卫星A转过一个周期时，下列关于三个卫星的说法正确的是

　　A. 三卫星的位置仍然在一直线上

　　B. 卫星A的位置超前于B,卫星C位置滞后于B

　　C. 卫星A的位置滞后于B,卫星C位置超前于B

　　D. 卫星A的位置滞后于B、C　

  5. 惯性制导系统已广泛应用与弹道式导弹工程中，这个系统的重要元件之一是加速度计。加速度计的构造原理的示意图如图所示：沿导弹长度方向安装的固定光滑杆上套一质量为m的滑块，滑块两侧分别与劲度系数均为k的弹簧相连．两弹簧的另一端与固定壁相连．滑块原来静止，弹簧处于自然长度．滑块上有指针，可通过标尺测出滑块的位移，然后通过控制系统进行制导．设某段时间内导弹沿水平方向飞行，指针向左偏离O点的距离为s，则这段时间内导弹的加速度

　　A. 方向向左，大小为1ks/m　

　　B. 方向向右，大小为1ks/m　

　　C. 方向向左，大小为2ks/m　　

　　D. 方向向右，大小为2ks/m　

　6. 为训练宇航员习惯失重，需要创造失重环境.在地球表面附近，可以在飞行器的座舱内短时间地完成失重.设某一飞机可作多种模拟飞行，令飞机于速率500m/s时进入试验状态，而速率为1000m/s时退出试验，则可以实现试验目的且有效训练时间最长的飞行是

　　A. 飞机在水平面内做变速圆周运动，速度由500m/s增加到1000m/s

　　B. 飞机在坚直面内沿圆孤俯冲，速度由500m/s增加到1000m/s( 在最低点)

　　C. 飞机以500m/s作竖直上抛运动（关闭发动机）,当它竖直下落速度增加到1000m/s时，开动发动机退出实验状态

　　D. 飞机以500m/s沿某一方向作斜抛或平抛运动（关闭发动机）,当速度达到1000m/s时开动发动机退出实验状态。

　7. 已知下面的哪组数据，可以计算出地球的质量（万有引力常数已知）：

　　A. 月球绕地球运行的周期及月球到地球中心的距离

　　B. 地球“同步卫星”离地面的高度

　　C. 地球绕太阳运行的周期及地球到太阳中心的距离

　　D. 人造地球卫星在地面附近的运行速度　　　　　　　　　　 

  8. 正在运转的机械，当其飞轮以角速度ω_o匀速转动时，机械的振动不强烈，切断电源，飞轮的转动逐渐慢下来，在某一小段时间内机器却发生了强烈的振动.此后飞轮转速继续变慢，机器的振动也随之减弱。在机器停下来之后重新启动机器,使飞轮转动的角速度从零较缓慢地增加，在这个过程中

　  A. 机器不一定还会发生强烈的振动

　  B. 机器一定还会发生强烈的振动

　　C. 若机器发生强烈的振动，强烈振动可能发生在飞轮的角速度为ω_o时

　　D. 若机器发生强烈的振动，强烈振动时的飞轮的角速度可能大于ω_o

  9. 一个小孩站在船头，如图所示，两种情况用同样大小的拉力拉绳子，经过相同的时间t（船未碰）则

　　A. 小孩对绳子拉力的冲量I₁<I₂

　　B. 小孩与船A整体经过时间t后的动量p₁<p₂

　　C. 小孩所做的功W₁=W₂

　　D. 在时刻t小孩拉绳的即时功率P₁<P₂

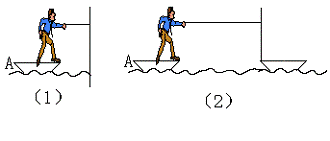
  10. 一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B。支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内摩擦转动，如图所示，开始时OA边处于水平位置，由静止释放，则以下说法错误的是

　　A. A球的最大速度为

　　B. A球速度最大时，两小球的总重力势能最小

　　C. A球速度最大时，两直角边与竖直方向的夹角为45°

　　D. A、B两球的最大速度之比

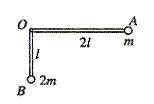
  11. 如图所示，有四列简谐波同时沿x轴正方向传播，波速分别是 v、2 v、3 v和 4 v，a、b是x轴上所给定的两点，且ab＝l。在t时刻a、b两点间四列波的波形分别如图所示，则由该时刻起a点出现波峰的先后顺序依次是图　　　　　　　 ；频率由高到低的先后顺序依次是图　　　　　　　 。

　　 A　　　　　　 B　　　　　　　 C　　　　　　　 D

  12. 飞行员从俯冲状态往上拉时,会发生黑视,第一是因为血压降低,导致视网膜缺血；第二是因为大脑缺血,回答问题

　　（1）血压为什么会降低?

　　（2）血液在人体循环中所起的作用是什么?

　　（3）为了使飞行员适应这种情况,要对飞行员进行训练,飞行员坐在一个垂直水平面做匀速圆周运动的舱内,要使飞行员的加速度达到6g,则转动速度需为多少?(设旋转半径为R=20m)

  13. 利用打点计时器研究一个约1. 4高的商店卷帘窗的运动。将纸带粘在卷帘底部，纸带通过打点计时器随帘在竖直面内向上运动。打印后的纸带如图所示，数据如表格所示。纸带中AB、BC、CD……每两点之间的时间间隔为0.10s，根据各间距的长度，可计算出卷帘窗在各间距内的平均速度V_平均。可以将V_平均近似地作为该间距中间时刻的即时速度V。

　　（1）请根据所提供的纸带和数据，绘出卷帘窗运动的V-t图线。

　　（2）AD段的加速度为　　　 ，AK段的平均速度为　　  。

　

　14. 宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L，若抛出时的初速增大到2倍，则抛出点与落地点之间的距离为L，已知两落地R，万有引力常数为G，求该星球的质量M。

【试题答案】

  1. C　2. D　3. C　4. B　5. D　6. C　7. A　8. B　9. D　10. A

  11. BDCA，DBCA

　12. (1)当飞行员往上加速时,血液处于超重状态,心脏无法像平常一样运输血液,导致血压降低.(2)血液循环的作用是提供氧气、营养，带走代谢产生的废物.(3) 34.29m/s. (4)10⁶N

　13. 答案：（l）如图所示，

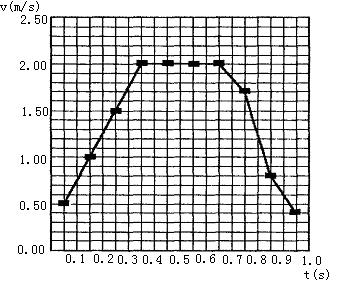
　　（2）5m/s²，1.39m/s

　14. 分析：根据平抛运动信息及规律，可得在该星球上物体的重力加速度，由重力与万有引力的关系可确定星球质量。

　　解答：设抛出点的高度为h，第一次平抛的水平射程为x

　　则x²+h²=L²

　　由平抛运动规律得知，当初速度增大到2v₀时，其水平射程也增大到2x，（h一定，t一定，）可得：

　　(2x) ²+h²=(L) ²　 (2)

　　由（1）、（2）解得h=

　　设该星球上的重力加速度为g，由平抛运动规律：h=gt²

　　有　（3）

　　由万有引力定律与牛顿第二定律，得：

　　

　　联立各式解得：

　　M=