● 郭文教

洛伦兹力做功特点应用浅议

一、洛伦兹力做功特点

洛伦兹力每时每该都与速度方向垂直，所以洛伦兹力对带电粒子不做功，它只起到改变带粒子运动方向的作用，不改变粒子的速率，也即不改变粒子的动能。

二、根据洛伦兹力做功的特点，用能的观点解决问题

带电粒子在复合场中做复杂的曲线运动时，如果不涉及求时间的问题，往往可以从能的角度出发去解决问题比较方便。

例1　如图1所示，质量为m，带电量为+q的粒子，从两平行电极板正中央垂直电场和磁场的方向以速度V飞入，已知两板间距为d，磁感应强度为B，这时粒子恰能直线穿过电场和磁场区域（不计重力），今将磁感应强度增大到某值。则粒子将落到极板上，求粒子落到极板上的动能。

解析：题中有两个物理情景，开始是粒子选择器模型，当粒子所受洛伦兹力等于电场力时，即，粒子不偏转，将磁感应强度增大后，洛伦兹力大于电场力，粒子向下偏，但不是类平抛运动，因为洛伦兹力方向时刻改变，不能用运动的合成与分解处理，又不是圆周运动，从力和运动的角度处理有困难，可抓住洛伦兹力不做功的特点，用能量观点处理。在整个过程中，电场力做负功为，设末动能为，用动能定理列方程可得：

解得：

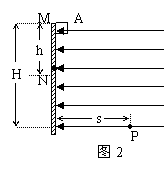
例2　如图2所示，匀强电场的场强，方向水平向左，匀强磁场的磁感应强度B=2T，方向垂直纸面向里，一个质量m=1g，带正电的小物块A从M点沿绝缘粗糙的竖直壁无初速下滑，当它滑行h=0.8m到N点时就离开壁做曲线运动.当A运动到P点时,恰好处于平衡状态,此时速度方向与水平方向成45⁰角，设P与M的高度差H=1.6m，求（1）A沿壁下滑时摩擦力做的功；（2）P与M的水平距离（g取10m/s²）。

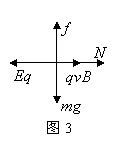
解析：分析A物体所做的运动可知，物体有三个运动过程：第一过程（MN）对粒子进行受力分析，如图3所示。列方程：

水平方向 …………①

竖直方向　…………②

当V增大N增大f增大a减小，所以MN物体A做a减小的加速运动，当物体到达N点时弹力N=0，物体离开竖直壁，这一阶段摩擦力做功，且摩擦力是变力，属于变力做功，以后离开壁后无摩擦力，所以只要求这一阶段就可以了，用能量观点处理。设摩擦做功为，到N点速度为V₁，重力做功，由动能定理得：…………③

在N点，当N=0时，有：…………④

解方程③④可得：

第二过程（NP）粒子做曲线运动，用能量观点处理，设到达P点后的速度V₂，物体A由NP过程中，只有重力做功和电场力做功，洛伦兹力不做功，由动能定理列方程：

…………⑤

第三过程（过P点后）是匀速直线运动，受力分析如图4所示，列平衡方程：

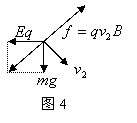
…………⑥

解方程可得，

三、洛伦兹力不做功应用时易引发的两种错误分析

1．洛伦兹力不做功，但洛伦兹力可引起其它力做功的变化

例3　如图所示，一个带正电荷的物体从粗糙斜面顶端滑到斜面底端时的速度为V，若再加上一个垂直纸面指向读者的磁场，则物体滑到底端时的速度将（　　　 ）

A．大于V　　　　　　　　　 B．小于V

C．等于V　　　　　　　　　 D．不能确定

错解：选C

解析：错解原因是部分同学认为洛伦兹力不做功就直接得出C，事实上，虽然洛伦兹力不做功，但随着物体垂直磁场向下滑，一旦加上磁场，就引起弹力比未加磁场时小，滑动摩擦力减小，滑到底端摩擦力做功减小，则滑到底端时的动能增大，速率增大，应该选A。

2．洛伦兹力不做功并非是不改变物体的运动状态

例4　如图6所示，在竖直绝缘的平台上，一个带正电的小球以水平速度V₀抛出，落到在地面上的A点，若加一垂直纸面向里的匀强磁场，则小球的落点（　　　　　 ）

A．仍在A点 　　　　　　　B．在A点左侧

C．在A点右侧　　　　　　D．无法确定

错解：选A，理由是洛伦兹力不做功，不改变小球的运动状态，故仍落在A点。

解析：事实上洛伦兹力虽不做功，俣可以改变小球的运动状态，可以改变速度的方向，小球做曲线运动，在运动中任一位置受力如图7所示，小球此时受到了斜向上的洛伦兹力的作用，小球在竖直方向的加速度，故小球平抛的时间将增加，落点应在A点的右侧。

浙江省金华市汤溪中学（321075）