高三物理第一次模拟题精编

1、[苏、锡、常、镇 16] 在广场游玩时，一个小孩将一充有氢气的气球用细绳系于一个小石块上，并将小石块放置于水平地面上．已知小石块的质量为m₁，气球（含球内氢气）的质量为m₂，气球体积为V，空气密度为ρ（V和ρ均视作不变量），风沿水平方向吹，风速为v．已知风对气球的作用力f＝ku（式中k为一已知系数，u为气球相对空气的速度）．开始时，小石块静止在地面上，如图所示．

　 （1）若风速v在逐渐增大，小孩担心气球会连同小石块一起被吹离地面，试判断是否会出现这一情况，并说明理由．

　 （2）若细绳突然断开，已知气球飞上天空后，在气球所经过的空间中的风速v保持不变量，求气球能达到的最大速度的大小．

[解答] （1）小石块不会被风吹离地面．以气球和小石块组成的系统为研究对象：地面对小石块支持力的大小为恒定，跟风速v无关．

　　（2）气球的最大水平速度等于风速，即v_xm＝v．

当竖直方向的合力为零时，竖直分速度最大，即

则

气球能达到的最大速度的大小为

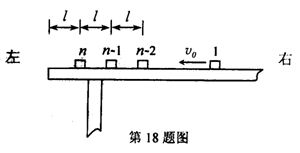
2、[苏、锡、常、镇 18]如图所示，n个相同的木块（可视为质点），每块的质量都是m，从右向左沿同一直线排列在水平桌面上，相邻木块间的距离均为l，第n个木块到桌边的距离也是l，木块与桌面间的动摩擦因数为µ．开始时，第1个木块以初速度v₀向左滑行，其余所有木块都静止，在每次碰撞后，发生碰撞的木块都粘在一起运动．最后第n个木块刚好滑到桌边而没有掉下．

　 （1）求在整个过程中因碰撞而损失的总动能．

　 （2）求第i次（i≤n－1）碰撞中损失的动能与碰撞前动能之比．

　 （3）若n＝４，l＝0.10m，v_0­＝3.0m/s，重力加速度g＝10m/s²，求µ的数值．

[解答] （1）整个过程中系统克服摩擦力做的总功为

W_f＝µmgl（1＋2＋3＋…＋n）＝

整个过程中因碰撞而损失的总动能为

（2）设第i次（i≤n－1）碰撞前瞬间，前i个木块粘合在一起的速度为v_i，动能为

　　

与第i＋１个（i≤n－1）木块碰撞粘合在一起后瞬间的速度为v_i＇，由动量守恒定律

　　

则

第i次（i≤n－1）碰撞中损失的动能为

　　

则第i次（i≤n－1）碰撞中损失的动能与碰撞前动能之比为

　　　　（i≤n－1）

（3）（常规解法）n＝４时，共发生了i＝3次碰撞．

第1次碰前瞬间的速度为，碰撞中动量守恒：

第1次碰后瞬间的速度为

第2次碰前瞬间的速度为

碰撞中动量守恒：

第2次碰后瞬间的速度为

第3次碰前瞬间的速度为

碰撞中动量守恒：

第3次碰后瞬间的速度为

最后滑行到桌边，速度恰好为零，则

即

整理后得，代入数据解得

3、[苏、锡、常、镇 17]在某一真空空间内建立xoy坐标系，从原点O处向第一象限发射一比荷的带正电的粒子（重力不计），速度大小v_0­＝10³m/s、方向与x轴正方向成30°角．

　 （1）若在坐标系y轴右侧加有匀强磁场区域，在第Ⅰ象限，磁场方向垂直xoy平面向外；在第Ⅳ象限，磁场方向垂直xoy平面向里；磁感应强度均为B＝1T，如图（a）所示．求粒子从O点射出后，第2次经过x轴时的坐标x₁．

　 （2）若将上述磁场改为如图（b）所示的匀强磁场．在t＝0到时，磁场方向垂直于xoy平面向外；在到时，磁场方向垂直于xoy平面向里，此后该空间不存在磁场．在t＝0时刻，粒子仍从O点以与原来相同的速度v₀射入，求粒子从O点射出后第2次经过x轴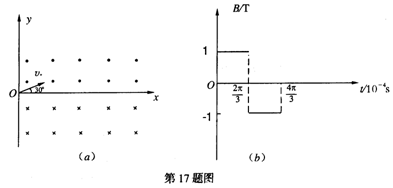时的坐标x₂．

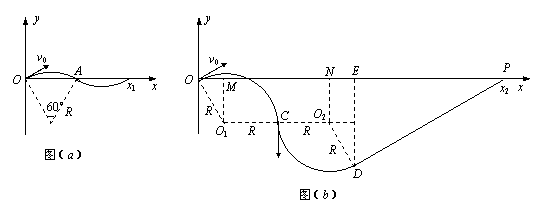
[解答] （1）轨迹如图（a）所示．轨迹半径，OA弧所对圆心角为60°，则OA＝R＝0.1ｍ，x₁＝2OA＝0.2m

（2）轨迹半径，周期，磁场变化的半周期为，轨迹如图（b）所示，由几何关系知∠OO₁C＝∠CO₂D＝120°，且O₁O₂平行于x轴，DE垂直于x轴．OE＝2（R＋Rsin30°）＝3R＝0.3ｍ．

rtΔEDP中，∠EDP＝60°，DE＝2Rsin60°，EP＝DEtan60°＝3R＝0.3ｍ．

则x₂＝OE＋EP＝0.6m

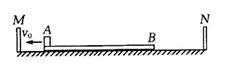
4、[徐州 18] 如图所示，质量为2kg的物块A(可看作质点)，开始放在长木板B的左端，B的质量为1kg，可在水平面上无摩擦滑动，两端各有一竖直挡板M N,现A、B以相同 的速度v₀=6m／s向左运动并与挡板M发生碰撞．B 与M碰后速度立即变为零，但不与M粘接；A与M碰撞没有能量损失，碰后接着返向N板运动，且在与N板碰撞之前，A、B均能达到共同速度并且立即被锁定，与N板碰撞后A、B一并原速反向，并且立刻解除锁定．A、B之间的动摩擦因数=0．1．通过计算求下列问题：

(1)A与挡板M能否发生第二次碰撞?

(2)A和最终停在何处?

(3)A在B上一共通过了多少路程?

[解答] (1)第一次碰撞后A以v_O=6 m／s速度向右运动，B的初速度为0，与N板碰前达共同速度v₁，则m_A v₀=(m_A+m_B)v₁　v₁=4m/s

系统克服阻力做功损失动能

　因与N板的碰撞没有能量损失，A、B与N板碰后返回向左运动，此时A的动能因此，当B先与M板碰撞停住后，A还有足够能量克服阻力做功，并与M板发生第二次碰撞．所以A可以与挡板M发生第二次碰撞。

　 (2)设第i次碰后A的速度为v_i，动能为E_Ai，达到共同速度后A的速度为v_i′动能为E_Ai′　同理可求

单程克服阻力做功

因此每次都可以返回到M板，景终停靠在M板前。

(3)由(2)的讨论可知，在每完成一个碰撞周期中损失的总能量均能满足

(即剩余能量为)

其中用以克服阻力做功占损失总能量之比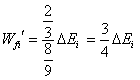

碰撞中能量损失所占的比例

因此，当初始A的总动能损失完时，克服摩擦力做的总功为

所以S＝27/2＝13.5m

5、[徐州 18]某同学在实验室先后完成下面二个实验：①测定一节干电池的电动势和内电阻；②描绘小灯泡的伏安特性曲线．

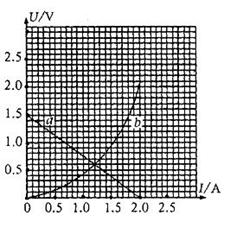　　(1)用①实验测量得到数据作出U一I图线如图中a线，实验所测干电池的电动势为　1.50　V，内电阻为　0.75　。

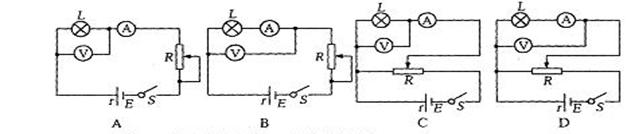
　  (2)在描绘小灯泡伏安特性曲线的实验中，为减小实验误差，方便调节，请在给定的四个电路图和三个滑动变阻器中选取适当的电路或器材，并将它们的编号填在横线上。应选取的电路是　C　，滑动变阻器应选取　E  。

E．总阻值15，最大允许电流2A的滑动变阻器

F．总阻值200，最大允许电流2A的滑动变阻器

G．总阻值1000，最大允许电流1A的滑动变阻器

(3)将实验②中得到的数据在实验①中同一U一I坐标系内描点作图，得到如图所示的图线乙，如果将实验①中的电池与实验②中的小灯泡组成闭合回路，此时小灯泡的实际功率为　0.72（±0.02）W，若将两节与实验①中相同的干电池串联后与该小灯泡组成闭合回路，则此时小灯泡的电压为0.85（0.85～0.88）V，实际功率为1.2W1.2～1.3W。

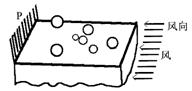
6、[江苏省常州中学 14] 如图所示，桌面上有许多大小不同的塑料球，它们的密度均为ρ，有水平向左恒定的风作用在球上；使它们做匀加速运动（摩擦不计），已知风对球的作用力与球的最大截面面积成正比，即F=kS(k为一常量).

(1)　对塑料球来说，空间存在一个风力场，请定义风力场强度及其表达式.

(2)　在该风力场中风力对球做功与路径无关，可引入风力势能和风力势的概念，若以栅栏P零风力势能参考平面，写出风力势能E_P和风力势U的表达式。

(3)写出风力场中机械能守恒定律的表达式.（球半径用r表示；第一状态速度为v₁，位置为x₁；第二状态速度为v₂，位置为x₂）

[解答] (1)风力场强度：风对小球的作用力与对小球最大截面积之比，即E=F/S=k

(2)距P为x处，E_P=Fx=kSx　　U=E_P/S=kS

(3)2ρrv₁²/3+kx₁=2ρrv₂²/3+kx₂

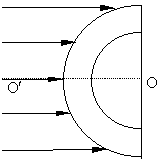7、 [江苏省常州中学 15]如图所示，用折射率的玻璃做成内径为R、外径为的半球形空心球壳，一束平行光射向此半球的外表面，与中心对称轴平行，试求：(1)球壳内部有光线射出的区域； (2)要使球壳内部没有光线射出，至少用多大的遮光板，如何放置才行?　

[解答] (1)设光线射入外球面，沿ab方向射向内球面，刚好发生全反射，则

∴　

在中，，

∴ 　，　

即 （1分），则

又 ，由 　　，得

∴ 　即

当射向外球面的入射光线的入射角小于时，这些光线都会射出内球面．因此，以为中心线，上、下（左、右）各的圆锥球壳内有光线射出．

（2）由图中可知，，所以，至少用一个半径为R的遮光板，圆心过轴并垂直该轴放置，才可以挡住射出球壳的全部光线，这时球壳内部将没有光线射出．