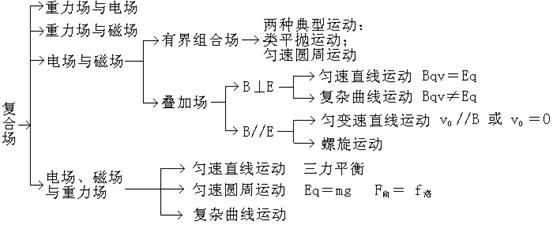
带电粒子在复合场中的运动-高中三年级物理试题练习、期中期末试卷、测验题、复习资料-高中物理试卷-试卷试题下载

专题复习：带电粒子在复合场中的运动

【一】备考目标

1．知识目标

（1）掌握带电粒子在各种场力作用下的运动特点的分析方法。

（2）理解速度选择器、质谱仪、回旋加速器、电磁流量计和等离子体发电机等的工作原理。

2．能力目标

（1）通过对带电粒子在电场、磁场、重力场中的受力分析、运动分析和能量分析比较，培养综合分析问题的能力。

（2）通过回旋加速器、质谱仪、速度选择器、电磁流量计和等离子体发电机等实际应用问题的分析，培养理论联系实际的能力。

【二】教学内容（本专题分为两节课讲解：①带电粒子在复合场中的受力分析、运动分析和能量分析；②带电粒子在复合场中的运动在生产、生活中的应用）

本专题复习内容是带电粒子在复合场中的运动，这类问题的显著特点是粒子的运动情况和轨迹较为复杂、抽象、多变，因而这部分习题最能考查学生综合分析问题的能力。在高考试题中多以带计算因素的选择题出现，在Ⅱ卷中的计算题中也时有出现，高考中对该考点的考查率接近100％，可见对该专题的复习在高考备考中尤为重要。

※复合场指电场、磁场和重力场三者或三者之二并存于同一空间时的场。

研究带电粒子在复合场中的运动所根据的规律、思路和方法一般与力学相同，故研究带电粒子的运动应先分析在复合场中的受力情况。

【问题1】对带电粒子的重力是否考虑，你是如何理解和判定的？

一般情况下，微观带电粒子（如：电子、质子、α粒子等）的重力不计；宏观带电粒子（如：带电的小球、带电的液滴等）的重力不能忽略；有些带电粒子的重力是否考虑，要根据题设条件进行判定。

【问题2】请根据你对三种场力的认识和理解，完成三种场力的比较

力种类比较量	电场力	洛伦兹力	重力
力的大小	① ②与电荷的运动状态无关，在匀强电场中，电场力为恒量	①电荷静止或运动方向与磁场方向平行，不受洛伦兹力 ②电荷运动方向与磁场方向垂直，洛伦兹力最大，	①G=mg ②与物体的运动状态无关
力的方向	正电荷受力方向与E方向相同负电荷受力方向与E方向相反	方向垂直于B、v所决定的平面，分清正负电荷后应用左手定则确定的指向	总是竖直向下
力做功特点	做功多少与电场中两点间电势差有关电场力做正功（负功），电荷电势能减少（增加）	洛伦兹力对电荷不做功，不能改变电荷速度的大小	做功多少路径无关，只取决于始、末位置的高度差 W＝mgh 重力做正功（负功），重力势能减少（增加）

启示：因重力和电场力做功与路径无关，洛仑滋力永不做功，所以可以利用动能定理求解

※几种典型的复合场的分析：

（一）电场与磁场

一、电场和磁场的有界组合场　

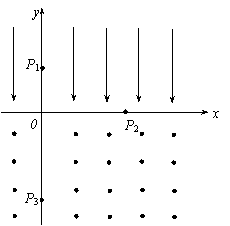例1、（04年高考物理·湖北理综卷·24）如图所示，在y＞0的空间中存在匀强电场，场强沿y轴负方向；在y＜0的空间中，存在匀强磁场，磁场方向垂直xy平面（纸面）向外。一电量为q、质量为m的带正电的运动粒子，经过y轴上y＝h处的点P₁时速率为v₀，方向沿x轴正方向；然后，经过x轴上x＝2h处的 P₂点进入磁场，并经过y轴上y＝处的P₃点。不计重力。求

（l）电场强度的大小。

（2）粒子到达P₂时速度的大小和方向。

（3）磁感应强度的大小。

参考答案：

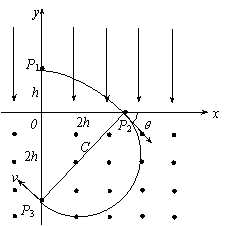
解：粒子在电场、磁场中运动的轨迹如图所示。设粒子从P₁到P₂的时间为t，电场强度的大小为E，粒子在电场中的加速度为a，由牛顿第二定律及运动学公式有：

qE ＝ ma　　　　　　 ①

v₀t ＝ 2h　　　　　　 ②

　　　　　　 ③

由①、②、③式解得：

　　　　　　 ④

（2）粒子到达P₂时速度沿x方向的分量仍为v₀，以v₁表示速度沿y方向分量的大小，v表示速度的大小，θ表示速度和x轴的夹角，则有：

　　　　　　　　　　　　　 ⑤

　　　　　　　　　　　　　 ⑥

　　　　　　　　　　　　 ⑦

由②、③、⑤式得：

v₁＝v₀　　　　　　　　　　　　　　 ⑧

由⑥、⑦、⑧式得：

　　　　　　　　　　　　　　　　⑨

　　　　　　　　　　　　　　　　　 ⑩

（3）设磁场的磁感应强度为B，在洛仑兹力作用下粒子做匀速圆周运动，由牛顿第二定律得：

　　　　　　　　　　　 ⑾

r是圆周的半径。此圆周与x轴和y轴的交点分别为P₂、P₃。因为OP₂＝OP₃，θ＝45°，由几何关系可知，连线P₂P₃为圆轨道的直径，由此可求得：

r＝　　　　　　　　　　　　　 ⑿

由⑨、⑾、⑿可得：

　　　　　　　　　　　　　　 ⒀

解题思路：若复合场是由电场和磁场组合而成，带电粒子则分别在两个区域中做类平抛运动和匀速圆周运动，通过连接点的速度将两种运动联系起来。一般可用类平抛运动和匀速圆周运动的运动规律求解。另外，准确画好运动轨迹图是解题的关键。

二、电场和磁场叠加

（1）B⊥E

① 匀速直线运动

速度选择器原理：Bqv＝Eq　 v＝E/B

② 复杂曲线运动

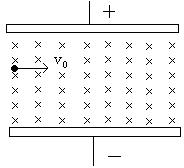
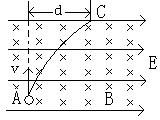例2、如图所示，场强为E的匀强电场和磁感应强度为B的匀强磁场相互正交，一个质子以速度v沿跟E、B都垂直的方向从A点射入，质子的电荷量为e，质量为m，当质子运动到C点时，偏离射入方向的距离为d，则质子在C点的动能为多少？

参考答案：

解：由动能定理可得：

质子在C点的动能为：

解题思路：若复合场是由电场和磁场叠加而成，B⊥E时，分两种情况：①当Eq＝Bqv时，带电粒子做匀速直线运动；②当Eq≠Bqv时，带电粒子做复杂的曲线运动，一般可用动能定理求解

（2）B//E

① 匀变速直线运动（匀加速或匀减速）

v₀//B 或 v₀＝0

② 螺旋运动

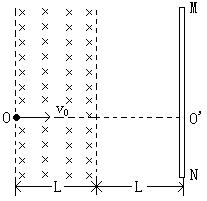例3、( 04年江苏南通市高三第二次调研·物理卷·17)如图所示，MN为一竖直放置足够大的荧光屏，距荧光屏左边的空间存在着一宽度也为、方向垂直纸面向里的匀强磁场。O’为荧光屏上的一点，OO’与荧光屏垂直，一质量为m、电荷量为q的带正电的粒子（重力不计）以初速度v₀从O点沿OO’方向射入磁场区域。粒子离开磁场后打到荧光屏上时，速度方向与竖直方向成30°角。

（1）求匀强磁场磁感应强度的大小和粒子打到荧光屏上时偏离O’点的距离；

（2）若开始时在磁场区域再加上与磁场方向相反的匀强电场（图中未画出），场强大小为E，则该粒子打到荧光屏上时的动能为多少？

参考答案：

（1）粒子从O点射入，P点射出，沿直线运动到荧光屏上的S点，如图所示，由几何关系可知，粒子在磁场中做匀速圆周运动转过的圆心角θ＝60°①

　　运动轨道半径为：R＝　　②

　　而qvB＝　③

　　由②③解得：B＝　④

　　根据几何关系可知：SQ＝°　⑤

　　O’O＝R－Rcos 60°　　　　 ⑥

由②⑤⑥解得：O’S＝O’Q＋SQ＝

（2）再加电场后，根据运动的独立性，带电粒子沿电场方向匀加速运动，运动速度

粒子在复合场中运动时间为：

则粒子离开复合场时沿电场方向运动的速度为

粒子打在荧光屏上的动能为：

【方法二：粒子离开复合场时沿电场方向运动的位移为

由动能定理可得：

粒子打到荧光屏上时的动能为：　】

解题思路：若复合场是由电场和磁场叠加而成，B//E时，分两种情况：①当v₀//B 或 v₀＝0时，带电粒子做匀变速直线运动；②当v₀⊥B时，带电粒子做螺旋运动（由匀变速直线运动和匀速圆周合成），一般可用运动的合成与分解求解（也可用动能定理求解）

（二）重力场、电场和磁场的复合场

若带电粒子同时受重力、电场力和洛仑滋力作用，请思考下面两个问题：

【问题3】带电粒子能否做直线运动？该直线运动一定是匀速直线运动吗？

答案：能　　一定。

【问题4】带电粒子能否做匀速圆周运动？若能，请你说明条件；若不能，请你说明理由。

答案：能，当重力与电场力平衡时，带电粒子可在洛伦兹力作用下做匀速圆周运动。

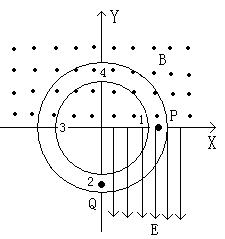例4、如图所示，用绝缘管做成的圆形轨道竖直放置，圆心与坐标原点重合，在Ⅰ、Ⅱ象限有垂直于纸面向外的匀强磁场，在第Ⅳ象限有竖直向下的匀强电场。一个带电荷量为＋q、质量为m的小球Q放在管中的最低点，另一个带电荷量也是＋q、质量也是m的小球P，从图中位置由静止释放开始运动，球P在最低点处与Q相碰并粘在一起向上滑，刚好能通过最高点。不计一切摩擦，电荷量保持不变，轨道半径为R，R远大于管道的内径，小球直径略小于管道内径，小球可看成质点，试求：（1）电场强度E；（2）若小球第二次到最高点时，刚好对轨道无压力，求磁感应强度B。