上学期高三同步测控优化训练物理：光的传播B卷-高中三年级物理试题练习、期中期末试卷、测验题、复习资料-高中物理试卷-试卷试题下载

高中同步测控优化训练(二)

第十九章　光的传播(B卷)

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.

第Ⅰ卷(选择题　共40分)

一、本题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的，请把它填在括号内.

1.假设在地球表面不存在大气层，那么白昼时间将会

A.变长　　　　　　　　　　　　　　　　　　　　　　　　　 B.变短

C.不变　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.无法确定

解析：本题考查太阳光线在大气层中的折射.由于地球大气层对太阳光线的折射，当人们看到太阳位于地平线上时，太阳的实际位置在地平线以下，因此假设地球表面不存在大气层时，白昼时间将会变短.故正确选项为B.

答案：B

2.目前，一种用于摧毁人造卫星或空间站的激光武器正在研制中.如图所示，某空间站位于地平线上方，现准备用一束激光射向该空间站，则应把激光器

A.沿视线对着空间站瞄高一些

B.沿视线对着空间站瞄低一些

C.沿视线对着空间站直接瞄准

D.条件不足，无法判断

解析：本题考查在光的折射现象中光路可逆.由于大气层对光线的折射，空间站的实际位置应在所看到的位置的下方，所以本题易错选B；但在折射现象中，由于光路可逆，所以应把激光器沿视线对着空间站直接瞄准.故正确选项为C.

答案：C

3.对下列自然现象描述正确的是

A.在海面上，向远方望去，有时能看到远方的景物悬在空中.同样，在沙漠中也能观察到同样的现象

B.在沙漠中，向远方望去，有时能看到远方景物的倒影.同样，在海面上也能观察到同样的现象

C.在海面上，向远方望去，有时能看到远方的景物悬在空中.在沙漠中，向远方望去，有时能看到远方景物的倒影

D.在海面上，向远方望去，有时能看到远方景物的倒影.在沙漠中，向远方望去，有时能看到远方的景物悬在空中

解析：本题考查两种不同的全反射现象.

夏天海面上的下层空气温度比上层低，密度比上层大，折射率也大，远处景物发出的光线射向空中时，由于不断被折射，越来越偏离法线方向，进入上层空气的入射角不断增大，以至于发生全反射.人们逆着光线看去，就会看到远处景物悬在空中.夏天沙漠里接近沙面的空气温度高，因而密度比上层的小，折射率也小，远处景物射向地面的光线进入折射率小的下层热空气层时被折射，入射角不断增大，也可能发生全反射.人们逆着反射的光线看去就会看到远处景物的倒影.

故C正确.

答案：C

4.如图所示，一细束红光与一细束蓝光平行射到同一个三棱镜上，经折射后交于光屏上的同一点M.若用n₁和n₂分别表示三棱镜对红光和蓝光的折射率，下列说法中正确的是

A.n₁＜n₂，a为红光，b为蓝光

B.n₁＜n₂，a为蓝光，b为红光

C.n₁＞n₂，a为红光，b为蓝光

D.n₁＞n₂，a为蓝光，b为红光

解析：本题考查光的折射.由图可知，b光线经过三棱镜后的偏折角较小，因此折射率较小，是红光.故正确选项为B.

答案：B

5.如图所示，一束白光以较大的入射角射到三棱镜的一侧面上，从三棱镜的另一侧面射出，在屏上形成从红到紫的彩色光带.当白光的入射角逐渐减小时

A.红光最先消失

B.紫光最先消失

C.红光和紫光同时消失

D.红光和紫光都不会消失

解析：本题考查色散及全反射.一束白光射入三棱镜后，从另一侧面折射时，可能发生全反射，而红光的临界角大，紫光的临界角小，当白光入射角减小，从另一侧面出射时，入射角逐渐增大，紫光先全反射.故正确选项为B.

答案：B

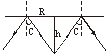
6.潜水员在折射率为的海水下h米深处，向上观察水面，能看到的天穹和周围的景物都出现在水面上的一个圆形面积为S的区域内.关于圆面积S和深度h的关系，正确的叙述是

A.S与水深h成正比

B.S与水深h成反比

C.S与水深h的平方成正比

D.S与水深h的平方成反比

解析：本题考查光的全反射.首先由题意可知最大入射角为90°，即折射角等于临界角，

sinC==则∠C=45°

如图所示，可知R=h

所以S=πR²=πh².

由上式可知正确选项为C.

答案：C

7.两井口大小和深度相同的井，一口是枯井，一口是水井(水面在井口之下)，两井底各有一只青蛙，则

A.枯井中青蛙觉得天比较小，水井中青蛙看到井外的范围比较大

B.枯井中青蛙觉得天比较大，水井中青蛙看到井外的范围比较小

C.枯井中青蛙觉得天比较大，水井中青蛙看到井外的范围比较大

D.两只青蛙觉得井口一样大，水井中青蛙看到井外的范围比较大

解析：本题考查折射现象.

光路图如图，青蛙在井底中央时，看到外界范围最大.由光路图可以看出，有水时，射入蛙眼的擦着井边的两条边缘光线夹角变小，即水中青蛙的视角变小，因而水中青蛙觉得井口小，觉得天较小；但进入水中青蛙眼睛的光线范围变大了，因而看到井外的范围比较大.故C正确.

答案：C

8.公园里灯光喷泉的水池中有处于同一深度的若干彩灯.在晚上观察不同颜色的彩灯的深度和水面上被照亮的面积，下列说法正确的是

A.红灯看起来较浅，红灯照亮的水面面积较小

B.红灯看起来较深，红灯照亮的水面面积较小

C.红灯看起来较浅，红灯照亮的水面面积较大

D.红灯看起来较深，红灯照亮的水面面积较大

解析：本题考查视深及光的全反射.设彩灯深度为h，色光折射率为n，则视深为h′=,由于红光折射率最小，所以红灯看起来较深.恰好发生全反射时的光路如图所示，由sinC=知，红光的临界角C最大，则红灯照亮的水面半径R=htanC最大，所以红灯照亮的水面面积S=πR²也最大.故正确选项为D.

答案：D

9.如图所示，两块同样的玻璃直角三棱镜ABC，两者的AC面是平行放置的，在它们之间是分布均匀的透明介质.一单色细光束O垂直于AB面入射，在图示的出射光线中

A.1、2、3(彼此平行)中的任一条都有可能

B.4、5、6(彼此平行)中的任一条都有可能

C.7、8、9(彼此平行)中的任一条都有可能

D.只能是4、6中的一条

解析：本题考查的是光折射及光通过平行板时，方向不变，只发生侧移.从整体上看，它像平行玻璃砖，但是它内部的光路又不同于整块玻璃砖.但从左边AB面射入的光和从右边AB面射出的光应该平行，选项A、C不正确.由中间介质的折射率知，B正确.所以正确选项为B.

答案：B

10.如图所示，用透明材料做成一长方体形的光学器材，要求从上表面射入的光线能从右侧面射出，那么所选的材料的折射率应满足

A.折射率必须大于

B.折射率必须小于

C.折射率可取大于1的任意值

D.无论折射率是多大都不可能

解析：本题考查光的折射及全反射.光路图如图所示，从图中可以看出，为使上表面射入的光线经两次折射后从右侧面射出，θ₁和θ₂都必须小于临界角C，即θ₁＜C,θ₂＜C,而θ₁+θ₂=90°，故C＞45°，则折射率n=1/sinC＜.故正确选项为B.

答案：B

第Ⅱ卷(非选择题　共60分)

二、本题共5小题,每小题4分，共20分.把答案填在题中的横线上或按题目要求作图.

11.若某介质的折射率为n，则从空气中射向该介质的光线，只有当入射角为_______时，反射光线才会与折射光线恰好垂直.

解析：本题考查光的折射和反射.

光路如图所示.

由题意知θ₁+θ₂=90°

由折射定律得

n===tanθ₁

则θ₁=arctann.

答案：arctann

12.如图所示是一块用折射率n=2的玻璃制成的透明体的横截面，ab是半径为R的圆弧，ac边与bc边垂直，∠aOc=60°.当一束平行黄色光垂直照到ac上时，ab部分的外表面只有一部分是黄亮的，其余是暗的.那么黄亮部分的弧长为_______.

解析：假定光线MN射到ab界面上时恰好发生全反射，则MN上方的光线一定在界面ab上发生全反射，因此只有射到界面Nb上的光线才能射出玻璃，界面Nb部分是亮的.由sinC=1/n得∠C=30°

由几何关系知θ=30°，所以弧Nb的长度：

s=30°/360°×2πR=πR/6

所以黄亮部分的弧长是πR/6.

答案：

13.一半圆形玻璃砖，玻璃的折射率为，AB为其直径，长度为D，O为圆心，一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖，其中心光线P通过O点，如图所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为_______.

解析：本题考查光的折射.光路如图所示.

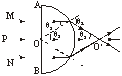
由几何关系知,边界光线在界面上的入射角θ₂=30°，由折射定律

得sinθ₁=nsinθ₂=

则折射角θ₁=60°

则OO′=2×cotθ₂=D.

答案：D

14.在日落很久以后，常能在高空中看到明亮的人造卫星.有一颗在地球赤道上方飞行的人造卫星，日落2 h后仍能在正上方看到它，它的最低高度(地球半径为6.38×10⁶ m)为_______.

解析：本题考查光的直线传播.若在地球北极上俯视，将看到地球做逆时针方向转动.如图所示，把人造地球卫星画在地球背光一侧上方，使它恰好被掠过地球表面的阳光照亮.从图可见，α角即为日落后地球转过的角度，h为最低高度

α=×360°=30°

h=R(-1)=6.38×10⁶×(-1) m=9.9×10⁵ m.

答案：9.9×10⁵ m

15.某同学在测一厚度均匀的圆形玻璃的折射率时，先在白纸上画一与圆形玻璃同半径的圆，圆心为O，将圆形玻璃平放在白纸上，使其边界与所画的圆重合.在玻璃一侧竖直插两枚大头针P₁和P₂,在另一侧按正确方法再插两枚大头针P₃和P₄，移去大头针和圆形玻璃后，得图如下：

(1)从P₃和P₄一侧观察时，P₁、P₂、P₃、P₄应满足的关系为__________________________；

(2)完成光路图，并标明入射光线、玻璃内传播的光线、出射光线；

(3)用α和β表示出光线从玻璃射出空气时的入射角和折射角，并用它们表示出玻璃的折射率为_______.

解析：(1)从P₃和P₄一侧观察，P₃、P₄和P₁、P₂的像应在一条直线上.

(2)连接P₁、P₂作为入射光线，延长至玻璃界面为入射点M；连接P₃、P₄作为出射光线，反向延长至玻璃界面为出射点N；连接M、N即为玻璃内传播的光线.

(3)连接O、N所作的直线是过出射点N点的界面法线，则入射角α和折射角β如图所示.由折射定律得：n=.

答案：(1)P₃、P₄和P₁、P₂的像在一条直线上

(2)略　(3)

三、本题共4小题，共40分.解答应写出必要的文字说明、方程式和重要演算步骤，只写出最后答案的不能得分.有数值计算的题，答案中必须明确写出数值和单位.

16.(8分)水对空气的折射率为.当在水面下放一强点光源时，可在水面上见到一个圆形透光平面.若光源在水面下2 m处，看到的透光平面的直径是多少？

解析：如图所示，光源为P，水面上见到的光即光源发出的光能从水中折射到空气中的部分.设该部分半径为r，直径为d，边缘光的入射角应等于临界角，即

sinC==　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (3分)

有tanC=1.134　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2分)

故r=htanC=2×1.134 m=2.27 m　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(2分)

则d=2r=2×2.27 m=4.54 m.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(1分)

答案：4.54 m

17.(10分)湖边有一高塔，两同学想不登塔而估测塔高.他们有两只小船、几只浮标和长卷尺.请简述他们的测量原理、步骤和需要测量的物理量，并用所测的物理量表示塔高.

解析：本题考查学生利用知识解决实际问题的能力.利用平面镜成像原理，甲同学划到湖内适当位置，立于船内目观湖内塔的倒影，并通知乙同学在塔影顶端水面位置放置一浮标.两同学协作测出甲同学的眼睛到水面的距离h₁、甲同学到浮标的距离s₁、浮标到塔底的距离s₂.设塔高为h₂(光路图如图)，由几何关系得：h₂/h₁=s₂/s₁，h₂=h₁s₂/s₁.故塔高为：h₁s₂/s₁.