高中物理定理、定律、公式表
一、质点的运动（1）------直线运动
1）匀变速直线运动
1.平均速度V平＝______（定义式） 2.有用推论__________
3.中间时刻速度Vt/2＝____＝__________ 4.末速度Vt＝__________
5.中间位置速度Vs/2＝___________ 6.位移s＝______＝__________＝________
7.加速度a＝________ ｛以Vo为正方向，a与Vo同向(a > 0)做_____运动；反向(a < 0)做_____运动｝
8.实验用推论Δs＝____ ｛Δs为连续相邻相等时间(T)内位移之差｝
9.主要物理量及单位:初速度(Vo):m/s； 加速度(a):m/s2； 末速度(Vt):m/s； 时间(t):秒(s)；
位移(s):米（m）； 路程:米； 速度单位换算：1m/s=3.6km/h。
注：(1)平均速度是矢量;
(2)物体速度大,加速度不一定大;
(3)a=(Vt-Vo)/t只是量度式，不是决定式;
(4)其它相关内容：质点、位移和路程、参考系、时间与时刻 / s--t图、v--t图 / 速度与速率、瞬时速度。
2)自由落体运动
1.初速度Vo＝___ 2.末速度Vt＝______
3.下落高度h＝________（从Vo位置向下计算） 4.推论Vt2＝______
注:(1)自由落体运动是初速度为___的________直线运动，遵循匀变速直线运动规律；
(2)a＝g＝9.8m/s2≈10m/s2（重力加速度在赤道附近较___,在高山处比平地___，方向__________）。
3)竖直上抛运动
1.位移s＝__________ 2.末速度Vt＝________ （g=9.8m/s2≈10m/s2）
3.有用推论Vt2-Vo2＝-2gs 4.上升最大高度Hm＝________ (抛出点算起）
5.往返时间t＝______ （从抛出落回原位置的时间）
注:(1)全过程处理:是________直线运动，以向上为正方向，加速度取___值；
(2)分段处理：向上为________直线运动，向下为__________运动，具有对称性；
(3)上升与下落过程具有对称性,如在同点速度等值反向等。
二、质点的运动（2）----曲线运动、万有引力
1)平抛运动
1.水平方向速度：Vx＝___ 2.竖直方向速度：Vy＝____
3.水平方向位移：x＝____ 4.竖直方向位移：y＝______
5.运动时间t＝________(通常又表示为(2h/g)1/2)
6.合速度Vt＝__________＝___________
合速度方向与水平夹角β:tgβ＝______＝______
7.合位移：s＝________,
位移方向与水平夹角α:tgα＝______＝________
8.水平方向加速度：ax=___；竖直方向加速度：ay＝___
注：(1)平抛运动是匀变速曲线运动，加速度为g，通常可看作是水平方向的________运动与竖直方向的__________运动的合成；
(2)运动时间由下落高度h(y)决定与水平抛出速度___关；
(3)θ与β的关系为tgβ＝___tgα；
(4)在平抛运动中时间t是解题关键；
(5)做曲线运动的物体必有加速度，当速度方向与所受合力(加速度)方向不在同一直线上时，物体做曲线运动。
2）匀速圆周运动
1.线速度V＝____＝______ 2.角速度ω＝____＝____＝____
3.向心加速度a＝____＝____＝_______ 4.向心力F心＝______＝______＝______＝______
5.周期与频率：T＝1/f 6.角速度与线速度的关系：V＝ωr
7.角速度ω与转速n的关系ω＝2πn(此处频率与转速意义相同)
8.主要物理量及单位：弧长(s):米(m)；角度(Φ)：弧度（rad）；频率（f）：赫（Hz）；周期（T）：秒（s）；转速（n）：r/s；半径(r):米（m）；线速度（V）：m/s；角速度（ω）：rad/s；向心加速度：m/s2。
注：（1）向心力可以由某个具体力提供，也可以由合力提供，还可以由分力提供，方向始终与速度方向____，指向______；
（2）做匀速圆周运动的物体，其向心力等于合力，并且向心力只改变速度的______，不改变速度的______，因此物体的动能保持不变，向心力不做功，但动量不断改变。
3)万有引力
1.开普勒第三定律：________＝K(＝4π2/GM)
｛R:轨道半径，T:周期，K:常量(与行星质量无关，取决于中心天体的质量)｝
2.万有引力定律：F＝_________ （G＝6.67×10-11N·m2/kg2，方向在它们的连线上）
3.天体上的重力和重力加速度：GMm/R2＝mg；g＝______ ｛R:天体半径(m)，M：天体质量（kg）｝
4.卫星绕行速度、角速度、周期：V＝________；ω＝________；T＝__________ ｛M：中心天体质量｝
5.第一(二、三)宇宙速度V1＝(g地r地)1/2＝(GM/r地)1/2＝_____km/s；V2＝_____km/s；V3＝______km/s
6.地球同步卫星GMm/(r地+h)2＝m4π2(r地+h)/T2 ｛h≈36000km，h:距地球表面的高度，r地:地球的半径｝
注:(1)天体运动所需的向心力由__________提供,F向＝____；
(2)应用万有引力定律可估算天体的质量、密度等；
(3)地球同步卫星只能运行于__________，运行周期和地球自转周期______；
(4)卫星轨道半径变小时,势能变___、动能变___、速度变___、周期变___、角速度变___、加速度变___；
(5)地球卫星的最大环绕速度和最小发射速度均为____km/s。
三、力（常见的力、力的合成与分解）
1）常见的力
1.重力G＝_____ （方向________，g＝9.8m/s2≈10m/s2，作用点在____，适用于地球表面附近）
2.胡克定律F＝____ ｛方向沿恢复形变方向，k：劲度系数(N/m)，x：形变量(m)｝
3.滑动摩擦力F＝______ ｛与物体相对运动方向______，μ：摩擦因数，FN：正压力(N)｝
4.静摩擦力0≤f静≤fm （与物体相对运动趋势方向______，fm为最大静摩擦力）
5.万有引力F＝______ （G＝6.67×10-11N·m2/kg2,方向在它们的连线上）
6.静电力F＝______ （k＝9.0×109N·m2/C2,方向在它们的连线上）
7.电场力F＝____ （E：场强N/C，q：电量C，正电荷受的电场力与场强方向相___）
8.安培力F＝________ （θ为B与L的夹角，当L⊥B时:F＝____，B//L时:F＝__）
9.洛仑兹力f＝_________ （θ为B与V的夹角，当V⊥B时：f＝____，V//B时:f＝__）
注:(1)劲度系数k由弹簧自身决定;
(2)摩擦因数μ与压力大小及接触面积大小无关，由接触面材料特性与表面状况等决定;
(3)fm略大于μFN，一般视为fm≈μFN;
(4)其它相关内容：静摩擦力（大小、方向）；
(5)物理量符号及单位：B：磁感强度(T)，L：有效长度(m)，I:电流强度(A)，V：带电粒子速度(m/s),
q:带电粒子（带电体）电量(C);
(6)安培力与洛仑兹力方向均用___手定则判定。
2）力的合成与分解
1.同一直线上力的合成 同向:F＝______， 反向：F＝______ (F1>F2)
2.互成角度力的合成：
F＝_______________ （余弦定理） F1⊥F2时:F＝__________
 |  | ||
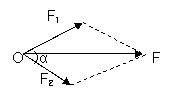3.合力大小范围：________≤F≤________
4.力的正交分解：Fx＝______，Fy＝______（β为合力与x轴之间的夹角tgβ＝______）
注：(1)力(矢量)的合成与分解遵循__________定则;
(2)合力与分力的关系是等效替代关系,可用合力替代分力的共同作用,反之也成立;
(3)除公式法外，也可用作图法求解,此时要选择标度,严格作图;
(4)F1与F2的值一定时,F1与F2的夹角(α角)越大，合力越___;
(5)同一直线上力的合成，可沿直线取正方向，用正负号表示力的方向，化简为代数运算。
四、动力学（运动和力）
1.牛顿第一运动定律(惯性定律）：物体具有惯性，总保持匀速直线运动状态或静止状态,直到有外力迫使它改变这种状态为止
2.牛顿第二运动定律： F合＝______ 或 a＝______ {由合外力决定,与合外力方向______}
3.牛顿第三运动定律：F＝-F´
{负号表示方向相反,F、F´各自作用在对方，平衡力与作用力反作用力区别，实际应用：反冲运动}
4.共点力的平衡F合＝0，推广
｛正交分解法、三力汇交原理｝
5.超重： FN ___ G， 失重：FN ___G { 加速度方向向___，均失重，加速度方向向___，均超重 }
6.牛顿运动定律的适用条件：
适用于解决低速运动问题，适用于宏观物体，不适用于处理高速问题，不适用于微观粒子
注:平衡状态是指物体处于______或__________状态。
五、振动和波（机械振动与机械振动的传播）
1.简谐振动F＝_____ {F:回复力，k:比例系数，x:位移，负号表示F的方向与x始终反向}
2.单摆周期T＝__________ ｛l:摆长(m)，g:当地重力加速度值，成立条件:摆角θ<100;l>>r｝
3.受迫振动频率特点：f＝________
4.发生共振条件:f驱动力___f固，A＝max， 共振的防止和应用
5.机械波、横波、纵波
6.波速v＝____＝____＝____ {波传播过程中，一个周期向前传播一个波长；波速大小由__________所决定}
7.声波的波速(在空气中）0℃：332m/s；20℃:344m/s；30℃:349m/s；声波是___波
8.波发生明显衍射（波绕过障碍物或孔继续传播）条件：障碍物或孔的尺寸比波长___，或者相差不大
9.波的干涉条件：两列波频率______(相差恒定、振幅相近、振动方向相同)
10.多普勒效应:由于波源与观测者间的相互运动，导致波源发射频率与接收频率不同
｛相互接近，接收频率______，反之，______｝
注：(1)物体的固有频率与振幅、驱动力频率无关，取决于振动系统本身；
(2)加强区是_____________或____________相遇处，减弱区则是____________相遇处；
(3)波只是传播了振动，介质本身不随波发生迁移,是传递能量的一种方式；
(4)干涉与衍射是波特有的；
(5)振动图象与波动图象；
(6)其它相关内容：超声波及其应用 / 振动中的能量转化。
六、冲量与动量(物体的受力与动量的变化）
1.动量：p＝____ ｛p:动量(kg/s)，m:质量(kg)，v:速度(m/s)，方向与速度方向相同｝
3.冲量：I＝____ ｛I:冲量(N·s)，F:恒力(N)，t:力的作用时间(s)，方向由F决定｝
4.动量定理：I＝Δp或____＝____ - ____o {Δp:动量变化Δp＝mvt–mvo，是矢量式}
5.动量守恒定律：p前总＝p后总或p＝p´也可以是______+______＝______+______
6.弹性碰撞：Δp＝0；ΔEK＝0 {即系统的动量和动能均守恒}
7.非弹性碰撞Δp＝0；0<ΔEK<ΔEKm {ΔEK：损失的动能，EKm：损失的最大动能}
8.完全非弹性碰撞Δp＝0；ΔEK＝ΔEKm {碰后连在一起成一整体}
9.物体m1以v1初速度与静止的物体m2发生弹性正碰:
v1´＝(m1-m2)v1/(m1+m2) v2´＝2m1v1/(m1+m2)
10.由9得的推论-----等质量弹性正碰时二者交换速度(动能守恒、动量守恒)
11.子弹m水平速度vo射入静止置于水平光滑地面的长木块M，并嵌入其中一起运动时的机械能损失
E损=mvo2/2-(M+m)vt2/2＝fs相对 {vt:共同速度，f:阻力，s相对子弹相对长木块的位移}
注：(1)正碰又叫对心碰撞，速度方向在它们“中心”的连线上;
(2)以上表达式除动能外均为矢量运算,在一维情况下可取正方向化为代数运算;
(3)系统动量守恒的条件:合外力为零或系统不受外力，则系统动量守恒（碰撞问题、爆炸问题、反冲问题等）;
(4)碰撞过程(时间极短，发生碰撞的物体构成的系统)视为动量守恒,原子核衰变时动量守恒;
(5)爆炸过程视为动量守恒，这时化学能转化为动能，动能增加；
(6)其它相关内容：反冲运动、火箭、航天技术的发展和宇宙航行。
七、功和能（功是能量转化的量度）
1.功：W＝________（定义式） ｛W:功(J)，F:恒力(N)，s:位移(m)，α:F、s间的夹角｝
2.重力做功：Wab＝________ {m:物体的质量，g＝9.8m/s2≈10m/s2，hab：a与b高度差(hab＝ha-hb)}
3.电场力做功：Wab＝______ ｛q:电量（C），Uab:a与b之间电势差(V)即Uab＝___－___｝
4.电功：W＝______ （普适式） ｛U：电压（V），I:电流(A)，t:通电时间(s)｝
5.功率：P＝____(定义式) ｛P:功率[瓦(W)]，W:t时间内所做的功(J)，t:做功所用时间(s)｝
6.汽车牵引力的功率：P＝____；P平均＝______ {P:瞬时功率，P平均:平均功率}
7.汽车以恒定功率启动、以恒定加速度启动、汽车最大行驶速度(vmax＝P额/f)
8.电功率：P＝____(普适式) ｛U：电路电压(V)，I：电路电流(A)｝
9.焦耳定律：Q＝______ ｛Q:电热(J)，I:电流强度(A)，R:电阻值(Ω)，t:通电时间(s)｝
10.纯电阻电路中I＝____；P＝______＝______＝______；Q＝___＝______＝_______＝______
11.动能：Ek＝______ ｛Ek:动能(J)，m：物体质量(kg)，v:物体瞬时速度(m/s)｝
12.重力势能：EP＝_____ ｛EP :重力势能(J)，g:重力加速度，h:竖直高度(m)(从零势能面起)｝
*13.电势能：EA＝qφA ｛EA:带电体在A点的电势能(J)，q:电量(C)，φA:A点的电势(V)(从零势能面起)｝
14.动能定理(对物体做正功,物体的动能______)：W合＝______ - ______或W合＝ΔEK
｛W合:外力对物体做的总功，ΔEK:动能变化ΔEK＝(mvt2/2-mvo2/2)｝
15.机械能守恒定律：ΔE＝0 或 ___ + ___＝___ + ___也可以是______ + ______＝______ + ______
16.重力做功与重力势能的变化(重力做功等于物体重力势能增量的负值) WG＝-ΔEP
注:(1)功率大小表示做功______,做功多少表示能量转化______；
(2)O0≤α<90O 做___功；90O<α≤180O做___功；α＝90o不做功(力的方向与位移（速度）方向垂直时该力不做功)；
(3)重力（弹力、电场力、分子力）做正功，则重力（弹性、电、分子）势能________；
(4)重力做功和电场力做功均与路径___关（见2、3两式）；
(5)机械能守恒成立条件：除重力（弹力）外其它力不做功，只是动能和势能之间的转化；
(6)能的其它单位换算:1kWh(度)＝__________ J，1eV＝__________ J；
*(7)弹簧弹性势能E＝kx2/2，与劲度系数和形变量有关。
八、分子动理论、能量守恒定律
1.阿伏加德罗常数NA＝______________ ；分子直径数量级____米
2.油膜法测分子直径d＝______ ｛V:单分子油膜的体积(m3)，S:油膜表面积(m2)｝
3.分子动理论内容：物质是由大量分子组成的；大量分子做无规则的热运动；分子间存在相互作用力。
4.分子间的引力和斥力(1)r<r0，f引___f斥，F分子力表现为___力
(2)r＝r0，f引___f斥，F分子力＝___，E分子势能＝Emin(最小值)
(3)r>r0，f引___f斥，F分子力表现为___力
(4)r>10r0，f引＝f斥≈0，F分子力≈0，E分子势能≈0
5.热力学第一定律：ΔU＝________
｛(做功和热传递，这两种改变物体内能的方式，在效果上是等效的)，W > 0:外界对物体做的___功(J)，Q > 0:物体______热量(J)，ΔU > 0:内能______(J)，涉及到第一类永动机不可造出｝
6.热力学第二定律
克氏表述：不可能使热量由低温物体传递到高温物体，而不引起其它变化（热传导的方向性）；
开氏表述：不可能从单一热源吸收热量并把它全部用来做功，而不引起其它变化（机械能与内能转化的方向性）｛涉及到第二类永动机不可造出｝
7.热力学第三定律：热力学零度不可达到｛宇宙温度下限：－273.15摄氏度（热力学零度）｝
注:(1)布朗粒子不是分子,布朗颗粒越____，布朗运动越明显,温度越____越剧烈；
(2)温度是分子__________的标志；
(3)分子间的引力和斥力同时存在,随分子间距离的增大而______ ,但斥力减小得比引力____；
(4)分子力做正功，分子势能________ ,在r0处F引___F斥且分子势能最_____；
(5)气体膨胀,外界对气体做___功 W___0；温度升高，内能______ΔU___0；吸收热量，Q___0；
(6)物体的内能是指物体内所有分子的__________和__________的总和，对于理想气体分子间作用力为零，分子势能为____；
(7)r0为分子处于平衡状态时，分子间的距离；
(8)其它相关内容：能的转化和定恒定律/能源的开发与利用、环保/物体的内能、分子的动能、分子势能。
九、气体的性质
1.气体的状态参量：
温度：宏观上，物体的冷热程度；微观上，物体内部分子无规则运动的剧烈程度的标志，
热力学温度与摄氏温度关系：T＝t+273 K ｛T:热力学温度(K)，t:摄氏温度(℃)｝
体积V：气体分子所能占据的空间的体积，单位换算：1m3＝____ L＝____ mL
压强p：单位面积上，大量气体分子频繁撞击器壁而产生持续、均匀的压力，
标准大气压：1atm ＝1.013×105 Pa ＝76cmHg ( 1Pa ＝1N/m2 )
2.气体分子运动的特点：分子间空隙大；除了碰撞的瞬间外，相互作用力微弱；分子运动速率很大
*3.理想气体的状态方程： p1V1/T1＝p2V2/T2 ｛PV/T＝恒量，T为热力学温度(K)｝
注:(1)理想气体的内能与理想气体的体积无关,与温度和物质的量有关；
(2)公式3成立条件均为一定质量的理想气体，使用公式时要注意温度的单位，t为摄氏温度(℃)，而T为热力学温度(K)。
十、电场
1.两种电荷、电荷守恒定律、元电荷：(e＝1.60×10-19C）；带电体电荷量等于元电荷的_________
2.库仑定律：F＝________ （在真空中）
｛F:点电荷间的作用力(N)，k:静电力常量k＝9.0×109N·m2/C2，Q1、Q2:两点电荷的电量(C)，r:两点电荷间的距离(m)，方向在它们的______上，作用力与反作用力，同种电荷互相______，异种电荷互相______｝
3.电场强度：E＝______（定义式、计算式)
｛E:电场强度(N/C)，是矢量（电场的叠加原理），q：检验电荷的电量(C)｝
4.真空点（源）电荷形成的电场E＝______ ｛r：源电荷到该位置的距离（m），Q：源电荷的电量｝
5.匀强电场的场强E＝______ ｛UAB:AB两点间的电压(V)，d:AB两点在场强方向的距离(m)｝
6.电场力：F＝____ ｛F:电场力(N)，q:受到电场力的电荷的电量(C)，E:电场强度(N/C)｝
7.电势与电势差：UAB＝___-___，UAB＝______＝-ΔEAB/q
8.电场力做功：WAB＝______＝______
｛WAB:带电体由A到B时电场力所做的功(J)，q:带电量(C)，UAB:电场中A、B两点间的电势差(V)(电场力做功与路径无关),E:匀强电场强度,d:两点沿场强方向的距离(m)｝
*9.电势能： EA＝qφA ｛EA:带电体在A点的电势能(J)，q:电量(C)，φA:A点的电势(V)｝
10.电势能的变化ΔEAB＝EB-EA ｛带电体在电场中从A位置到B位置时电势能的差值｝
11.电场力做功与电势能变化ΔEAB＝-WAB＝-qUAB (电势能的增量等于电场力做功的负值)
12.电容C＝_____(定义式,计算式) ｛C:电容(F)，Q:电量(C)，U:电压(两极板电势差)(V)｝
13.平行板电容器的电容C＝__________ （S:两极板正对面积，d:两极板间的垂直距离，ω：介电常数）
常见电容器
14.带电粒子在电场中的加速(Vo＝0)：W＝ΔEK 或 qU＝mVt2/2， Vt＝(2qU/m)1/2
15.带电粒子沿垂直电场方向以速度Vo进入匀强电场时的偏转(不考虑重力作用的情况下)
类平抛 ______电场方向:匀速直线运动L＝Vot(在带等量异种电荷的平行极板中：E＝U/d)
运动 ______电场方向:初速度为零的匀加速直线运动d＝at2/2，a＝F/m＝qE/m
注:(1)两个完全相同的带电金属小球接触时,电量分配规律:原带异种电荷的先_____后_____,原带同种电荷的总量______；
(2)电场线从___电荷出发终止于___电荷,电场线不相交,切线方向为场强方向,电场线密处场强___,顺着电场线电势越来越___,电场线与等势线______；
(3)常见电场的电场线分布要求熟记；
(4)电场强度（矢量）与电势（标量）均由________决定,而电场力与电势能还与带电体带的电量多少和电荷正负有关；
(5)处于静电平衡导体是个_____,表面是个______,导体外表面附近的电场线______导体表面，导体内部合场强为___,导体______没有净电荷,净电荷只分布于导体____表面；
(6)电容单位换算：1F＝____μF＝_____pF；
(7）电子伏(eV)是能量的单位,1eV＝__________J；
(8)其它相关内容：静电屏蔽 / 示波管、示波器及其应用 / 等势面。
十一、恒定电流
1.电流强度：I＝______ ｛I:电流强度(A），q:在时间t内通过导体横载面的电量(C），t:时间(s）｝
2.欧姆定律：I＝______ ｛I:导体电流强度(A)，U:导体两端电压(V)，R:导体阻值(Ω)｝
3.电阻、电阻定律：R＝________ ｛ρ:电阻率(Ω·m)，L:导体的长度(m)，S:导体横截面积(m2)｝
4.闭合电路欧姆定律：I ＝________ 或 E＝________ 也可以是E ＝________
｛I:电路中的总电流(A)，E:电源电动势(V)，R:外电路电阻(Ω)，r:电源内阻(Ω)｝
5.电功与电功率：W＝______，P＝______ ｛W:电功(J)，U:电压(V)，I:电流(A)，t:时间(s)，P:电功率(W)｝
6.焦耳定律：Q＝______ ｛Q:电热(J)，I:通过导体的电流(A)，R:导体的电阻值(Ω)，t:通电时间(s)｝
7.纯电阻电路中: 由于I＝U/R , W＝Q，因此W＝Q＝________＝_________＝_________
8.电源总动率、电源输出功率、电源效率：P总＝______，P出＝______，η＝______=______
｛I:电路总电流(A)，E:电源电动势(V)，U:路端电压(V)，η：电源效率｝
9.电路的串/并联 串联电路(P、U与R成___比) 并联电路(P、I与R成___比)
电阻关系 R串＝R1+R2+R3+ 1/R并＝1/R1+1/R2+1/R3+
电流关系 I总＝I1＝I2＝I3 I并＝I1+I2+I3+
电压关系 U总＝U1+U2+U3+ U总＝U1＝U2＝U3
功率分配 P总＝P1+P2+P3+ P总＝P1+P2+P3+
10.欧姆表测电阻
(1)电路组成 (2)测量原理
两表笔短接后,调节Ro使电表指针满偏，得
Ig＝E /(r + Rg + Ro)
接入被测电阻Rx后通过电表的电流为
Ix＝E /(r+Rg+Ro+Rx)＝E/(R中+Rx)
由于Ix与Rx对应，因此可指示被测电阻大小
(3)使用方法:机械调零、选择量程、短接欧姆调零、测量读数
｛注意挡位(倍率)｝、拨off挡。
(4)注意:测量电阻时，要与原电路断开,选择量程使指针在中
央附近,每次换挡要重新短接欧姆调零。
11.伏安法测电阻
电流表___接法： 电流表___接法：
 | |||
 | |||
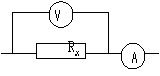电压表示数：U＝UR+UA 电流表示数：I＝IR+IV
Rx的测量值＝U/I＝(UA+UR)/IR＝RA+Rx___R真 Rx的测量值＝U/I＝UR/(IR+IV)＝RVRx/(RV+R)___R真
选用电路条件Rx___RA [或Rx___(RARV)1/2] 选用电路条件Rx___RV [或Rx___(RARV)1/2]
12.滑动变阻器在电路中的限流接法与分压接法
限流接法
 |
电压调节范围___,电路简单,功耗小 电压调节范围___,电路复杂,功耗较大
便于调节电压的选择条件Rp > Rx 便于调节电压的选择条件Rp < Rx
注:(1)单位换算：1A＝103mA＝106μA； 1kV＝103V＝106mA； 1MΩ＝103kΩ＝106Ω
(2)各种材料的电阻率都随温度的变化而变化,金属电阻率随温度升高而______；
(3)串联总电阻大于任何一个分电阻,并联总电阻小于任何一个分电阻；
(4)当电源有内阻时,外电路电阻增大时,总电流______,路端电压______；
(5)当外电路电阻等于电源电阻时,电源输出功率______,此时的输出功率为________；
(6)其它相关内容：电阻率与温度的关系 / 半导体及其应用 / 超导及其应用。
十二、磁场
1.磁感应强度是用来表示磁场的______和______的物理量,是___量，单位:(T),1T＝1N/A·m
2.安培力F＝______ (注：L⊥B) {B:磁感应强度(T),F:安培力(F),I:电流强度(A),L:导线长度(m)}
3.洛仑兹力f＝______(注：V⊥B); 质谱仪 ｛f:洛仑兹力(N)，q:带电粒子电量(C)，V:带电粒子速度(m/s)｝
4.在重力忽略不计(不考虑重力)的情况下,带电粒子进入磁场的运动情况(掌握两种)：
(1)带电粒子沿______磁场方向进入磁场:不受洛仑兹力的作用,做匀速直线运动V＝V0
(2)带电粒子沿______磁场方向进入磁场:做匀速圆周运动,规律如下:
(a)F向＝f洛＝mV2/r＝mω2r＝m (2π/T)2r＝qVB；r＝________；T＝________；
(b)运动周期与圆周运动的半径和线速度___关,洛仑兹力对带电粒子不做功(任何情况下)；
(c)解题关键:画轨迹、找圆心、定半径、圆心角（＝二倍弦切角）。
注：(1)安培力和洛仑兹力的方向均可由___手定则判定，只是洛仑兹力要注意带电粒子的正负；
(2)磁感线的特点及其常见磁场的磁感线分布要掌握〔见图〕；
(3)其它相关内容：地磁场 / 磁电式电表原理 / 回旋加速器 / 磁性材料分子电流假说。
十三、电磁感应
1.感应电动势的大小计算公式
1)E＝__________（普适公式）
｛法拉第电磁感应定律，E：感应电动势(V)，n：感应线圈匝数，ΔΦ/Δt:磁通量的变化率｝
2)E＝_________ ｛L:有效长度(m)，θ：L 和v的夹角｝
3)Em＝__________（交流发电机最大的感应电动势） ｛Em:感应电动势峰值｝
4)E＝__________（导体一端固定以ω旋转切割） ｛ω:角速度(rad/s)，V:速度(m/s)｝
2.磁通量Φ＝______ {Φ:磁通量(Wb),B:匀强磁场的磁感应强度(T),S:正对面积(m2) , θ：B和S的夹角}
3.感应电动势的正负极可利用感应电流方向判定 ｛电源内部的电流方向：由___极流向___极｝
*4.自感电动势E自＝nΔΦ/Δt＝LΔI/Δt ｛L:自感系数(H)(线圈L有铁芯比无铁芯时要___)，ΔI:变化电流，∆t:所用时间，ΔI/Δt:自感电流变化率(变化的快慢)｝
注：(1)感应电流的方向可用楞次定律或___手定则判定，楞次定律应用要点；
(2)自感电流总是______引起自感电动势的电流的变化；
(3)单位换算：1H＝____mH＝____μH。
(4)其它相关内容：自感 / 日光灯。
十四、交变电流（正弦式交变电流）
1.电压瞬时值e＝___________ 电流瞬时值i＝___________；(ω＝2πf)
2.电动势峰值Em＝__________＝________ 电流峰值(纯电阻电路中)Im＝______
3.正(余)弦式交变电流有效值：E＝______；U＝______；I＝_______
4.理想变压器原副线圈中的电压与电流及功率关系U1/U2＝______；I1/I2＝_______；P入___P出
5.在远距离输电中,采用高压输送电能可以减少电能在输电线上的损失:P损´＝________；
（P损´:输电线上损失的功率，P:输送电能的总功率，U:输送电压，R:输电线电阻）；
6.公式1、2、3、4中物理量及单位：ω:角频率(rad/s)；t:时间(s)；n:线圈匝数；B:磁感强度(T)；
S:线圈的面积(m2)；U:(输出)电压(V)；I:电流强度(A)；P:功率(W)。
注:(1)交变电流的变化频率与发电机中线圈的转动的频率相同即:ω电＝ω线，f电＝f线；
(2)发电机中,线圈在中性面位置磁通量最___,感应电动势为___,过中性面电流方向就______；
(3)有效值是根据电流________定义的,没有特别说明的交流数值都指______值；
(4)理想变压器的匝数比一定时,输__电压由输__电压决定,输__电流由输__电流决定，输入功率____输出功率,当负载的消耗的功率增大时输入功率也______，即P__决定P__；
(5)其它相关内容：正弦交流电图象 / 电阻、电感和电容对交变电流的作用。
十五、电磁振荡和电磁波
1.LC振荡电路T＝_________；f＝1/T ｛f:频率(Hz)，T:周期(s)，L:电感量(H)，C:电容量(F)｝
2.电磁波在真空中传播的速度c＝3.00×108m/s，λ＝______ ｛λ:电磁波的波长(m)，f:电磁波频率｝
注:(1)在LC振荡过程中,电容器电量最大时，振荡电流_______；电容器电量为零时，振荡电流______；
(2)麦克斯韦电磁场理论:______的电(磁)场产生磁(电)场；
(3)其它相关内容：电磁场 / 电磁波 / 无线电波的发射与接收 / 电视、雷达。
十六、光的反射和折射（几何光学）
1.反射定律α＝i ｛α;反射角，i:入射角｝
2.绝对折射率(光从真空中到介质)n＝______＝________
｛光的色散，可见光中红光折射率___，n:折射率，c:真空中的光速，v:介质中的光速，
:入射角，
:折射角｝
3.全反射：1)光从介质中进入真空或空气中时发生全反射的临界角C：sinC＝______
2)全反射的条件：光___介质射入光___介质；入射角______或______临界角
注:(1)平面镜反射成像规律:成______、______的___像,像与物沿平面镜______；
(2)三棱镜折射成像规律:成___像,出射光线向______偏折,像的位置向______偏移；
(3)光导纤维是光的________的实际应用,放大镜是___透镜,近视眼镜是___透镜；
(4)熟记各种光学仪器的成像规律,利用反射(折射)规律、光路的可逆等作出光路图是解题关键；
(5)白光通过三棱镜发色散规律：紫光靠近______出射。
十七、光的本性（光既有______性,又有______性,称为光的波粒二象性）
1.两种学说:微粒说(牛顿)、波动说(惠更斯)
2．双缝干涉:中间为___条纹；亮条纹位置:
＝nλ；暗条纹位置:＝(2n+1)λ/2（n＝0,1,2,3,、、、）；
条纹间距
｛:路程差(光程差)；λ:光的波长；λ/2:光的半波长；d两条狭缝间的距离；l：挡板与屏间的距离｝
3.光的颜色由光的______决定,光的频率由______决定,与介质___关,光的传播速度与介质___关，光的颜色
按频率从低到高的排列顺序是：___、___、___、___、___、___、___ (助记：___光的频率大，波长小)
4.薄膜干涉:增透膜的厚度是绿光在薄膜中波长的______,即增透膜厚度d＝______
5.光的衍射：光在没有障碍物的均匀介质中是沿直线传播的，在障碍物的尺寸比光的波长___得多的情况下，光的衍射现象不明显可认为沿直线传播，反之，就不能认为光沿直线传播
6.光的偏振：光的偏振现象说明光是___波
7.光的电磁说：光的本质是一种________。电磁波谱(按波长从___到___排列):无线电波、红外线、可见光、
紫外线、伦琴射线、γ射线。 红外线、紫外、线伦琴射线的发现和特性、产生机理、实际应用
8.光子说,一个光子的能量E＝______ ｛h:普朗克常量＝6.63×10-34J.s，ν:光的频率｝
9.爱因斯坦光电效应方程：____________ ｛mVm2/2:光电子初动能，hν:光子能量，W:金属的逸出功｝
注:(1)要会区分光的干涉和衍射产生原理、条件、图样及应用,如双缝干涉、薄膜干涉、单缝衍射、圆孔衍射、圆屏衍射等；
(2)其它相关内容:光的本性学说发展史 / 泊松亮斑 / 发射光谱 / 吸收光谱 / 光谱分析 / 原子特征谱线 / 光电效应的规律 光子说 / 光电管及其应用 / 光的波粒二象性 / 激光 / 物质波。
十八、原子和原子核
1.α粒子散射实验结果:(a)______数的α粒子不发生偏转；
(b)___数α粒子发生了较大角度的偏转；
(c)______数α粒子出现大角度的偏转(甚至反弹回来)
2.原子核的大小：____～____m，原子的半径约____m (原子的核式结构)
3．光子的发射与吸收：原子发生定态跃迁时,要辐射(或吸收)一定频率的光子:hν＝E初-E末｛能级跃迁｝
4.原子核的组成：质子和中子（统称为___子）
｛A＝______数＝______数＋______数，Z=______数＝______数＝__________数＝_________数｝
5.天然放射现象：α射线（α粒子是________）、β射线（____运动的______）、γ射线（波长极__的电磁波）、
α衰变与β衰变、半衰期(有半数的原子核发生了衰变所用的时间)。
γ射线是伴随α射线和β射线产生的
6.爱因斯坦的质能方程:E＝______ ｛E:能量(J)，m:质量(Kg)，c:光在真空中的速度｝
7.核能的计算ΔE＝________
｛当Δm的单位用kg时，ΔE的单位为___；当Δm用原子质量单位u时，算出的ΔE单位为____；
1uc2＝________MeV｝
注:(1)常见的核反应方程(重核裂变、轻核聚变等核反应方程)要求掌握；
(2)熟记常见粒子的质量数和电荷数；
(3)质量数和电荷数守恒,依据实验事实,是正确书写核反应方程的关键；
(4)其它相关内容:氢原子的能级结构 / 氢原子的电子云 / 放射性同位素及其应用、放射性污染和防护 /重核裂变、链式反应、链式反应的条件、核反应堆 / 轻核聚变、可控热核反应 / 人类对物质结构的认识。