高三物理第一次综合练习试卷2006.09
（试卷满分100分，考试时间为100分钟）
一、本题共1６小题；每小题3分，共４８分。在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。全部选对的得3分，选不全的得2分，有选错或不答的得0分。把选出的答案填在答题纸上的相应表格内。
1．如图所示，细绳OA、OB共同吊起质量为m的物体．OA与OB互相垂直．OB与竖直墙成60°角，OA、OB对O点的拉力分别为
、
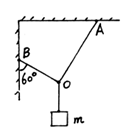A．、的合力大小为mg，方向竖直向上
B．、的合力与物体的重力是一对平衡力
C．
D．
2．从某一高度先后由静止释放两个相同的小球甲和乙，若两球被释放的时间间隔为1s，在不计空气阻力的情况下，它们在空中的运动过程中（ ）
A．甲、乙两球的距离越来越大，甲、乙两球的速度之差越来越大
B．甲、乙两球的距离始终保持不变，甲、乙两球的速度之差保持不变
C．甲、乙两球的距离越来越大，甲、乙两球的速度之差保持不变
D．甲、乙两球的距离越来越小，甲、乙两球的速度之差越来越小
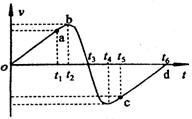3．一个小孩在蹦床上作游戏，他从高处落到蹦床上后又被弹起到原高度．小孩从高处开始下落到弹回的整个过程中，他的运动速度随时间变化的图象如图所示，图中oa段和cd段为直线．则根据此图象可知，小孩和蹦床相接触的时间为
A．t2～t4
B．t1～t4
C．t1～t5
D．t2～t5
4．把物体以一定速度水平抛出。不计空气阻力，g取10
，那么在落地前的任意一秒内
A．物体的末速度大小一定等于初速度大小的10倍
B．物质的末速度大小一定比初速度大10
C．物体的位移比前一秒多10m
D．物体下落的高度一定比前一秒多10m
5．原来做匀速运动的升降机内，具有一定质量的物体A静止在地板上，其与升降机的侧壁间有一被压缩的弹簧，如图所示.现发现A突然被弹簧推向左方．由此可判断，此时升降机的运动可能是
( )
A．加速上升 B．减速上升
C．加速下降 D．减速下降
6．一个做简谐运动的弹簧振子，周期为T，设t1时刻振子不在平衡位置，经过一段时间到t2时刻，振子的速度与t1时刻的速度大小相等、方向相同。若t2-t1<T/2，则
A．t2时刻振子的加速度一定跟t1时刻大小相等、方向相反
B．在（t1+t2）/2时刻，振子处在平衡位置
C．从t1到t2时间内，振子的运动方向不变
D．从t1到t2时间内，振子所受的回复力的方向不变
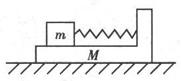7．放在水平地面上的物体M上表面有一物体m，m与M之间有一处于压缩状态的弹簧，整个装置处于静止状态，如图所示，则关于M和m受力情况的判断，正确的是
A．m受到向右的摩擦力
B．M受到m对它向左的摩擦力
C．地面对M的摩擦力方向右
D．地面对M不存在摩擦力作用
8．某物体受到一个－6N·s的冲量作用，则
A．物体的动量增量一定与规定的正方向相反
B．物体原来的动量方向一定与这个冲量的方向相反
C．物体的末动量方向一定与这个冲量的方向相反
D．物体的动量一定在减小
9．地球的两颗人造卫星质量之比m1：m2=1：2，圆运动轨道半径之比r1：r2=1：2，则
A．它们的线速度之比为v1：v 2=
B．它们的运动周期之比为T1：T 2=
C．它们的向心加速度之比为a1：a 2=4：1
D．它们的向心力之比为F1：F 2=4：1
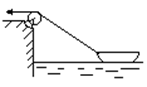
10．如图所示，人在岸上用轻绳拉船，若人匀速行进，则船将做
A．匀速运动 B．匀加速运动
C．变加速运动 D．减速运动
11．如图所示，在水平面上有一固定的U形金属框架，框架上置一金属杆ab，在垂直纸面方向有一匀强磁场，下面情况可能的是
A．若磁场方向垂直纸面向外，并且磁感应强度增大时，杆ab将向右移动
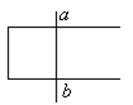B．若磁场方向垂直纸面向外，并且磁感应强度减小时，杆ab将向右移动
C．若磁场方向垂直纸面向里，并且磁感应强度增大时，杆ab将向右移动
D．若磁场方向垂直纸面向里，并且磁感应强度减小时，杆ab将向右移动
12．一辆汽车以恒定的功率沿倾角为30°的斜坡行驶，汽车所受的摩擦阻力等于车重的2倍，若车匀速上坡时速度为v，则它匀速下坡时的速率为
A．v B．
C．
v D．2v
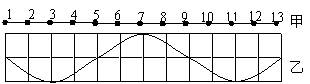13．在均匀介质中，各质点的平衡位置在同一直线上，相邻两质点的距离均为s，如图所示。振动从质点1开始向右传播，质点1开始运动时的速度方向竖直向上。经过时间t，前13个质点第一次形成如图乙所示的波形。关于这列波的周期和波速有如下说法
①这列波的周期T= 2t/3
②这亿波的周期T = t/2
③这列波的传播速度v = 12s/t
④这列波的传播速度v = 16s/t
上述说法正确的是
A．①③ B．①④ C．②③ D．②④
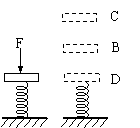14．如图所示,一原长为L0的轻质弹簧下端固定在水平地面上，其上端与一质量为m的重物相连接，当重物静止时，弹簧保持竖直方向，长度为L1。现用力缓慢竖直向下将重物压至D点，此时弹簧长度为L2，外力大小为F。然后撤去外力，重物将从静止开始沿竖直方向在D、C之间做简谐振动，B点是D、C的中点。已知重物运动到D点时弹簧的弹性势能为EP0，运动到B点时的物体的动能为EKB。则外力开始将重物压至D点的过程中所做的功为
A. EKB B. EP0 C. F(L0－L2) D. F(L1－L2)
15．如图所示，a、b是两个带有同种电荷的小球，用绝缘细线拴于同一点，两球静止时，它们离水平地面的高度相等，绳与竖直方向夹角为α、β，且α＜β。同时剪断细线，不计空气阻力，两球带电量不变，下列判断正确的是
A．两球质量相等
B． a、b同时落地
C．在空中飞行过程中，a、b都做平抛运动
D．落地时a球水平飞行的距离比b球小
16．如图所示，A、B是一对平行的金属板，在两板间加上一周期为T的交变电压u，A板的电势UA=0，B板的电势UB随时间变化规律为：在0到T/2的时间内，UB=U0(正的常数)；在T/2到T的时间内，UB=-U0；在T到3T/2的时间内，UB=U0；在3T/2到2T的时间内，UB=-U0……，现有一电子从A板上的小孔进入两板间的电场区内，设电子的初速度和重力的影响均可忽略，则
A．若电子是在t=0时刻进入的，它将一直向B板运动
B．若电子是在t=T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上
C．若电子是在t=3T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上
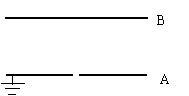D．若电子是在t=T/2时刻进入的，它可能时而向B板，时而向A板运动
二．本题共5小题，52分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题，答案中必须明确写出数值和单位。
17.(8分)有一星球其半径为地球半径的2倍，平均密度与地球相同，今把一台在地球表面走时准确的摆钟移到该星球表面，求摆钟的秒针走一圈的实际时间。
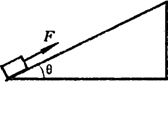18.(10分)如图所示，在倾角θ=370的足够长的固定的斜面底端有一质量m=1．0kg的物体，物体与斜面间动摩擦因数μ＝0.25。现用轻细绳将物体由静止沿斜面向上拉动，拉力F=10.ON，方向平行斜面向上。经时间t＝4．0s绳子突然断了，求：(1)绳断时物体的速度大小。(2)从绳子断了开始到物体再返回到斜面底端的运动时间。(sin37°=O.60，cos37°=O.80，g=10m/s2)
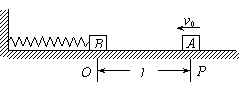19．（10分）如图，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上的O点，此时弹簧处于原长。另一质量与B相同的滑块A从导轨上的P点以初速度v0向B滑行，当A滑过距离l时，与B相碰。碰撞时间极短，碰后A、B粘在一起运动。设滑块A和B均可视为质点，与导轨的动摩擦因数均为μ。重力加速度为g。求：
（1）碰后瞬间，A、B共同的速度大小；
（2）若A、B压缩弹簧后恰能返回到O
点并停止，求弹簧的最大压缩量。
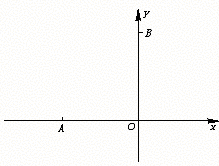20.(10分)如图所示，在xoy平面内有垂直坐标平面的范围足够大的匀强磁场，磁感强度为B，一带正电荷量Q的粒子，质量为ｍ，从Ｏ点以某一初速度垂直射入磁场，其轨迹与x、y轴的交点A、B到O点的距离分别为ａ、ｂ，试求：
(1)初速度方向与ｘ轴夹角θ．
(2)初速度的大小.
21.(14分)如图所示，在光滑水平面上有一质量为M，长为L的长木板，另一小物块质量为m，它与长木板间的动摩擦因数为μ，开始时，木板与小物块均靠在与水平面垂直的固定挡板处，以共同的速度v0向右运动，当长板与右边固定竖直挡板碰撞后，速度反向，大小不变，且左右挡板之间距离足够长。
(1)试求物块不从长木板上落下的条件。
(2)若上述条件满足，且M=2kg，m=1kg,v0=10m/s。试计算整个系统在第五次碰撞前损失的所有机械能。
参考答案：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | AC | C | C | D | BC | ABC | ABD | A | ABC | C |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| |||
| 答案 | BD | B | D | A | BD | AB |
| |||
17.地球质量为M0,地球半径为R0,地球的平均密度为
,地球表面的重力加速度为
.星球质量为M,星球半径为R,星球的平均密度为
,星球表面的重力加速度为
.
质量为m的物体在地球表面受到的重力
………………(1)
…………….(2)
摆长为L的单摆在地球表面时的周期为
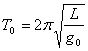…………………(3)
质量为
的物体在地球表面受到的重力
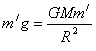………………(4)
…………….(5)
摆长为L的单摆在地球表面时的周期为
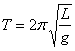…………………(6)
由题意
……………………..(7)
由以上各式得 
所以该星球表面摆钟的秒针走一圈的实际时间为
分
18. (1)物体受拉力向上运动过程中，受拉力F，重力mg摩擦力f，设物体向上运动的
加速度为a1，根据牛顿第二定律有
……………………………………………………(1)
因
…………………………………………………(2)
解得：
所以t=4.0s时物体的速度大小为v1=a1t=8.Om/s
(2)绳断时物体距斜面底端的位移
绳断后物体沿斜面向上做匀减速直线运动，设运动的加速度大小为
，则根据牛顿第二定律，对物体沿斜面向上运动的过程有
……………………………………(3)
解得
物体做减速运动的时间t2=v1/a2＝1.0s，减速运动的位移s2＝v1t2／2=4.Om
此后物体将沿斜面匀加速下滑，设物体下滑的加速度为a3，根据牛顿第二定律对物体
加速下滑的过程有mgsinθ—mgcos=ma3………………………(4)
解a3=4.0m/s2
设物体由最高点到斜面底端的时间为t3，所以物体向下匀加速运动的位移
所以物体返回到斜面底端的时间为t总=t2＋t3=4.2s
19.（1）设A、B质量均为m，A刚接触B时的速度为v1，碰后瞬间共同的速度为v2
以A为研究对象，从P到O，由功能关系
……………(1)
以A、B为研究对象，碰撞瞬间，由动量守恒定律
mv1 = 2mv2 ..................................(2)
解得 
……………….(3)
（2）碰后A、B由O点向左运动，又返回到O点，设弹簧的最大压缩量为x
由功能关系 μ ( 2mg )·2x = 
………….(4)
解得 
20．带电粒子运动的轨迹经过O、A、B三点，由几何关系可知，粒子做圆周运动轨迹的圆心坐标为（－a/2，b/2），初速度方向与ｘ轴夹角
θ＝arctg（a/b）。……………………………..(1)
由几何关系可知，轨道半径
R＝
……………………………………..(2)
又由
QVB＝mV2/R,………………………………………..(3)
解得 V＝
21.(1)设第一次碰撞后速度为v1，第n次碰撞后速度为vn，每次碰撞后，由于两挡板距离足够长，物块与长木板都能达到相对静止，第一次若不能掉下，往后每次滑动距离越来越短，更不可能掉下。由动量守恒定律和能量守恒定律知
(M-m)v0=(M+m)v1 …………………………….(1)
mgμL=
(m+M)
-(M+m)
………………(2)
由①②解得
当木板长大于L即可，即L≥
(2)第二次碰撞前，有(M-m)v0=(M+m)v1…….(3)
第三次碰撞前，(M-m)v1=(M+m)v2…………….(4)
第n次碰撞前 (M-m)vn-2=(M+m)vn-1………..(5)
vn-1=
………………………..(6)
第五次碰撞前
…………………(7)
故第五次碰撞前损失的总机械能为
代入数据
J