第六章 机械振动和机械波
一、简谐运动的基本概念
1.定义
物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。表达式为:F= -kx
⑴简谐运动的位移必须是指偏离平衡位置的位移。也就是说,在研究简谐运动时所说的位移的起点都必须在平衡位置处。
⑵回复力是一种效果力。是振动物体在沿振动方向上所受的合力。
⑶“平衡位置”不等于“平衡状态”。平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态)
⑷F=-kx是判断一个振动是不是简谐运动的充分必要条件。凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
2.几个重要的物理量间的关系
要熟练掌握做简谐运动的物体在某一时刻(或某一位置)的位移x、回复力F、加速度a、速度v这四个矢量的相互关系。
⑴由定义知:F∝x,方向相反。
⑵由牛顿第二定律知:F∝a,方向相同。
⑶由以上两条可知:a∝x,方向相反。
⑷v和x、F、a之间的关系最复杂:当v、a同向(即 v、 F同向,也就是v、x反向)时v一定增大;当v、a反向(即 v、 F反向,也就是v、x同向)时,v一定减小。
3.从总体上描述简谐运动的物理量
振动的最大特点是往复性或者说是周期性。因此振动物体在空间的运动有一定的范围,用振幅A来描述;在时间上则用周期T来描述完成一次全振动所须的时间。
⑴振幅A是描述振动强弱的物理量。(一定要将振幅跟位移相区别,在简谐运动的振动过程中,振幅是不变的而位移是时刻在改变的)
⑵周期T是描述振动快慢的物理量。(频率f=1/T
也是描述振动快慢的物理量)周期由振动系统本身的因素决定,叫固有周期。任何简谐振动都有共同的周期公式:![]() (其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
(其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
二、典型的简谐运动
1.弹簧振子
⑴周期![]() ,与振幅无关,只由振子质量和弹簧的劲度决定。
,与振幅无关,只由振子质量和弹簧的劲度决定。
⑵可以证明,竖直放置的弹簧振子的振动也是简谐运动,周期公式也是![]() 。这个结论可以直接使用。
。这个结论可以直接使用。
⑶在水平方向上振动的弹簧振子的回复力是弹簧的弹力;在竖直方向上振动的弹簧振子的回复力是弹簧弹力和重力的合力。
![]() 例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
解:该振动的回复力是弹簧弹力和重力的合力。在平衡位置弹力和重力等大反向,合力为零;在平衡位置以下,弹力大于重力,F- mg=ma,越往下弹力越大;在平衡位置以上,弹力小于重力,mg-F=ma,越往上弹力越小。平衡位置和振动的振幅大小无关。因此振幅越大,在最高点处小球所受的弹力越小。极端情况是在最高点处小球刚好未离开弹簧,弹力为零,合力就是重力。这时弹簧恰好为原长。
⑴最大振幅应满足kA=mg, A=![]()
⑵小球在最高点和最低点所受回复力大小相同,所以有:Fm-mg=mg,Fm=2mg
2.单摆。
⑴单摆振动的回复力是重力的切向分力,不能说成是重力和拉力的合力。在平衡位置振子所受回复力是零,但合力是向心力,指向悬点,不为零。
 ⑵当单摆的摆角很小时(小于5°)时,单摆的周期
⑵当单摆的摆角很小时(小于5°)时,单摆的周期![]() ,与摆球质量m、振幅A都无关。其中l为摆长,表示从悬点到摆球质心的距离,要区分摆长和摆线长。
,与摆球质量m、振幅A都无关。其中l为摆长,表示从悬点到摆球质心的距离,要区分摆长和摆线长。
⑶小球在光滑圆弧上的往复滚动,和单摆完全等同。只要摆角足够小,这个振动就是简谐运动。这时周期公式中的l应该是圆弧半径R和小球半径r的差。
⑷摆钟问题。单摆的一个重要应用就是利用单摆振动的等时性制成摆钟。在计算摆钟类的问题时,利用以下方法比较简单:在一定时间内,摆钟走过的格子数n与频率f成正比(n可以是分钟数,也可以是秒数、小时数……),再由频率公式可以得到:
![]()
![]()
例2. 已知单摆摆长为L,悬点正下方3L/4处有一个钉子。让摆球做小角度摆动,其周期将是多大?
 解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,周期分别为
解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,周期分别为![]() 和
和![]() ,因此该摆的周期为 :
,因此该摆的周期为 :![]()
 例3. 固定圆弧轨道弧AB所含度数小于5°,末端切线水平。两个相同的小球a、b分别从轨道的顶端和正中由静止开始下滑,比较它们到达轨道底端所用的时间和动能:ta__tb,Ea__2Eb。
例3. 固定圆弧轨道弧AB所含度数小于5°,末端切线水平。两个相同的小球a、b分别从轨道的顶端和正中由静止开始下滑,比较它们到达轨道底端所用的时间和动能:ta__tb,Ea__2Eb。
解:两小球的运动都可看作简谐运动的一部分,时间都等于四分之一周期,而周期与振幅无关,所以ta= tb;从图中可以看出b小球的下落高度小于a小球下落高度的一半,所以Ea>2Eb。
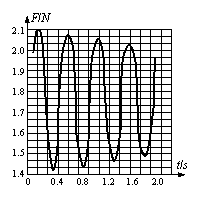
例4. 将一个力电传感器接到计算机上,可以测量快速变化的力。用这种方法测得的某单摆摆动过程中悬线上拉力大小随时间变化的曲线如右图所示。由此图线提供的信息做出下列判断:①t=0.2s时刻摆球正经过最低点;②t=1.1s时摆球正处于最高点;③摆球摆动过程中机械能时而增大时而减小;④摆球摆动的周期约是T=0.6s。上述判断中正确的是
A.①③ B.②④ C.①② D.③④
解:注意这是悬线上的拉力图象,而不是振动图象。当摆球到达最高点时,悬线上的拉力最小;当摆球到达最低点时,悬线上的拉力最大。因此①②正确。从图象中看出摆球到达最低点时的拉力一次比一次小,说明速率一次比一次小,反映出振动过程摆球一定受到阻力作用,因此机械能应该一直减小。在一个周期内,摆球应该经过两次最高点,两次最低点,因此周期应该约是T=1.2s。因此答案③④错误。本题应选C。
三、受迫振动与共振
1.受迫振动
物体在驱动力(既周期性外力)作用下的振动叫受迫振动。
⑴物体做受迫振动的频率等于驱动力的频率,与物体的固有频率无关。
⑵物体做受迫振动的振幅由驱动力频率和物体的固有频率共同决定:两者越接近,受迫振动的振幅越大,两者相差越大受迫振动的振幅越小。
2.共振
当驱动力的频率跟物体的固有频率相等时,受迫振动的振幅最大,这种现象叫共振。
要求会用共振解释现象,知道什么情况下要利用共振,什么情况下要防止共振。
⑴利用共振的有:共振筛、转速计、微波炉、打夯机、跳板跳水、打秋千……
⑵防止共振的有:机床底座、航海、军队过桥、高层建筑、火车车厢……
例5. 把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛。不开电动机让这个筛子自由振动时,完成20次全振动用15s;在某电压下,电动偏心轮的转速是88r/min。已知增大电动偏心轮的电压可以使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。为使共振筛的振幅增大,以下做法正确的是
A.降低输入电压 B.提高输入电压
C.增加筛子质量 D.减小筛子质量
解:筛子的固有频率为f固=4/3Hz,而当时的驱动力频率为f驱=88/60Hz,即f固< f驱。为了达到振幅增大,应该减小这两个频率差,所以应该增大固有频率或减小驱动力频率。本题应选AD。
四、机械波
1.分类
机械波可分为横波和纵波两种。
⑴质点振动方向和波的传播方向垂直的叫横波,如:绳上波、水面波等。
⑵质点振动方向和波的传播方向平行的叫纵波,如:弹簧上的疏密波、声波等。
2.机械波的传播
⑴在同一种均匀介质中机械波的传播是匀速的。波速、波长和频率之间满足公式:v=λžf。
⑵介质质点的运动是在各自的平衡位置附近的简谐运动,是变加速运动,介质质点并不随波迁移。
⑶机械波转播的是振动形式、能量和信息。
⑷机械波的频率由波源决定,而传播速度由介质决定。
3.机械波的反射、折射、干涉、衍射
一切波都能发生反射、折射、干涉、衍射。特别是干涉、衍射,是波特有的性质。
⑴干涉。产生干涉的必要条件是:两列波源的频率必须相同。
需要说明的是:以上是发生干涉的必要条件,而不是充分条件。要发生干涉还要求两列波的振动方向相同(要上下振动就都是上下振动,要左右振动就都是左右振动),还要求相差恒定。我们经常列举的干涉都是相差为零的,也就是同向的。如果两个波源是振动是反向的,那么在干涉区域内振动加强和减弱的位置就正好颠倒过来了。
干涉区域内某点是振动最强点还是振动最弱点的充要条件:
①最强:该点到两个波源的路程之差是波长的整数倍,即δ=nλ
②最弱:该点到两个波源的路程之差是半波长的奇数倍,即![]()
根据以上分析,在稳定的干涉区域内,振动加强点始终加强;振动减弱点始终减弱。
至于“波峰和波峰叠加得到振动加强点”,“波谷和波谷叠加也得到振动加强点”,“波峰和波谷叠加得到振动减弱点”这些都只是充分条件,不是必要条件。
 例6. 如图所示,S1、S2是两个相干波源,它们振动同步且振
例6. 如图所示,S1、S2是两个相干波源,它们振动同步且振
幅相同。实线和虚线分别表示在某一时刻它们所发出的波的
波峰和波谷。关于图中所标的a、b、c、d四点,下列说法
中正确的有
A.该时刻a质点振动最弱,b、c质点振动最强,d质点振
动既不是最强也不是最弱
B.该时刻a质点振动最弱,b、c、d质点振动都最强
C.a质点的振动始终是最弱的, b、c、d质点的振动始终是最强的
D.再过T/4后的时刻a、b、c三个质点都将处于各自的平衡位置,因此振动最弱
解:该时刻a质点振动最弱,b、c质点振动最强,这不难理解。但是d既不是波峰和波峰叠加,又不是波谷和波谷叠加,如何判定其振动强弱?这就要用到充要条件:“到两波源的路程之差是波长的整数倍”时振动最强,从图中可以看出,d是S1、S2连线的中垂线上的一点,到S1、S2的距离相等,所以必然为振动最强点。
描述振动强弱的物理量是振幅,而振幅不是位移。每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的。
本题答案应选B、C
⑵衍射。
发生明显衍射的条件是:障碍物或孔的尺寸和波长可以相比或比波长小。
⑶波的独立传播原理和叠加原理。
独立传播原理:几列波相遇时,能够保持各自的运动状态继续传播,不互相影响。
叠加原理:介质质点的位移、速度、加速度都等于几列波单独转播时引起的位移、速度、加速度的矢量和。
波的独立传播原理和叠加原理并不矛盾。前者是描述波的性质:同时在同一介质中传播的几列波都是独立的。比如一个乐队中各种乐器发出的声波可以在空气中同时向外传播,我们仍然能分清其中各种乐器发出的不同声波。后者是描述介质质点的运动情况:每个介质质点的运动是各列波在该点引起的运动的矢量和。这好比老师给学生留作业:各个老师要留的作业与其他老师无关,是独立的;但每个学生要做的作业却是所有老师留的作业的总和。
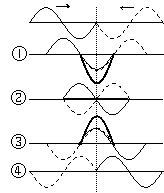 例7. 如图中实线和虚线所示,振幅、周期、起振方向都相同的两列正弦波(都只有一个完整波形)沿同一条直线向相反方向传播,在相遇阶段(一个周期内),试画出每隔T/4后的波形图。并分析相遇后T/2时刻叠加区域内各质点的运动情况。
例7. 如图中实线和虚线所示,振幅、周期、起振方向都相同的两列正弦波(都只有一个完整波形)沿同一条直线向相反方向传播,在相遇阶段(一个周期内),试画出每隔T/4后的波形图。并分析相遇后T/2时刻叠加区域内各质点的运动情况。
解:根据波的独立传播原理和叠加原理可作出每隔T/4后的波形图如①②③④所示。
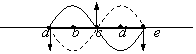 相遇后T/2时刻叠加区域内abcde各质点的位移都是零,但速度各不相同,其中a、c、e三质点速度最大,方向如图所示,而b、d两质点速度为零。这说明在叠加区域内,a、c、e三质点的振动是最强的,b、d两质点振动是最弱的。
相遇后T/2时刻叠加区域内abcde各质点的位移都是零,但速度各不相同,其中a、c、e三质点速度最大,方向如图所示,而b、d两质点速度为零。这说明在叠加区域内,a、c、e三质点的振动是最强的,b、d两质点振动是最弱的。
五、振动图象和波的图象
1.振动图象和波的图象
振动图象和波的图象从图形上看好象没有什么区别,但实际上它们有本质的区别。
⑴物理意义不同:振动图象表示同一质点在不同时刻的位移;波的图象表示介质中的各个质点在同一时刻的位移。
⑵图象的横坐标的单位不同:振动图象的横坐标表示时间;波的图象的横坐标表示距离。
⑶从振动图象上可以读出振幅和周期;从波的图象上可以读出振幅和波长。
2.波的图象的画法
波的图象中,波的图形、波的传播方向、某一介质质点的瞬时速度方向,这三者中已知任意两者,可以判定另一个。(口诀为“上坡下,下坡上” )
3.波的传播是匀速的
在一个周期内,波形匀速向前推进一个波长。n个周期波形向前推进n个波长(n可以是任意正数)。因此在计算中既可以使用v=λžf,也可以使用v=s/t,后者往往更方便。
4.介质质点的运动是简谐运动(是一种变加速运动)
任何一个介质质点在一个周期内经过的路程都是4A,在半个周期内经过的路程都是2A,但在四分之一个周期内经过的路程就不一定是A了。
5.起振方向
 介质中每个质点开始振动的方向都和振源开始振动的方向相同。
介质中每个质点开始振动的方向都和振源开始振动的方向相同。
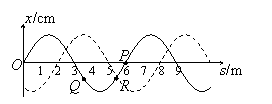
例8. 已知在t1时刻简谐横波的波形如图中实线所示;
在时刻t2该波的波形如图中虚线所示。t2-t1 = 0.02s
求:⑴该波可能的传播速度。⑵若已知T< t2-t1<2T,
且图中P质点在t1时刻的瞬时速度方向向上,求可
能的波速。⑶若0.01s<T<0.02s,且从t1时刻起,图中Q质点比R质点先回到平衡位置,求可能的波速。
解:⑴如果这列简谐横波是向右传播的,在t2-t1内波形向右匀速传播了![]() ,所以波速
,所以波速![]() =100(3n+1)m/s (n=0,1,2,…);同理可得若该波是向左传播的,可能的波速v=100(3n+2)m/s (n=0,1,2,…)
=100(3n+1)m/s (n=0,1,2,…);同理可得若该波是向左传播的,可能的波速v=100(3n+2)m/s (n=0,1,2,…)
⑵P质点速度向上,说明波向左传播,T< t2-t1 <2T,说明这段时间内波只可能是向左传播了5/3个波长,所以速度是唯一的:v=500m/s
⑶“Q比R先回到平衡位置”,说明波只能是向右传播的,而0.01s<T<0.02s,也就是T<0.02s<2T,所以这段时间内波只可能向右传播了4/3个波长,解也是唯一的:v=400m/s
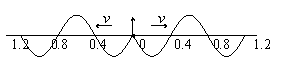
 例9. 在均匀介质中有一个振源S,它以50HZ的频率上下振动,该振动以40m/s的速度沿弹性绳向左、右两边传播。开始时刻S的速度方向向下,试画出在t=0.03s时刻的波形。
例9. 在均匀介质中有一个振源S,它以50HZ的频率上下振动,该振动以40m/s的速度沿弹性绳向左、右两边传播。开始时刻S的速度方向向下,试画出在t=0.03s时刻的波形。
解:从开始计时到t=0.03s经历了1.5个周期,波分别向左、右传播1.5个波长,该时刻波源S的速度方向向上,所以波形如右图所示。
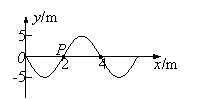 例10. 如图所示是一列简谐横波在t=0时刻的波形图,已知这列波沿x轴正方向传播,波速为20m/s。P是离原点为2m的一个介质质点,则在t=0.17s时刻,质点P的:①速度和加速度都沿-y方向;②速度沿+y方向,加速度沿-y方向;③速度和加速度都正在增大;④速度正在增大,加速度正在减小。
例10. 如图所示是一列简谐横波在t=0时刻的波形图,已知这列波沿x轴正方向传播,波速为20m/s。P是离原点为2m的一个介质质点,则在t=0.17s时刻,质点P的:①速度和加速度都沿-y方向;②速度沿+y方向,加速度沿-y方向;③速度和加速度都正在增大;④速度正在增大,加速度正在减小。
以上四种判断中正确的是
A.只有① B.只有④
C.只有①④ D.只有②③
解:由已知,该波的波长λ=4m,波速v=20m/s,因此周期为T=λ/v=0.2s;因为波向右传播,所以t=0时刻P质点振动方向向下;0.75 T <0.17s< T,所以P质点在其平衡位置上方,正在向平衡位置运动,位移为正,正在减小;速度为负,正在增大;加速度为负,正在减小。①④正确,选C
六、声波
1.声波是纵波。
2.空气中的声速可认为是340m/s,水中的声速是1450m/s,铁中的声速是4900m/s。
3.人耳可以听到的声波的频率范围是20Hz-20000Hz
4.人耳只能区分开相差0.1s以上的两个声音。