蕲春一中高三(9)测试题

一、选择题：1. 若a＞b＞c且a+b+c=0，则下列不等式恒成立的是(　　)

 (A)ab＞bc　　　(B)ac＞bc　　　　(C)ab＞ac　　　 (D)ab＞cb

2. 三棱锥的三条侧棱两两垂直，其长分别是,,1, 则其外接球的面积是

 (A)6p　　　　 (B)10p　　　　  (C)18p　　　　  (D)24p

3. 等差数列a₁,a₂,a₃,…,a_k中，已知a₄+a₇+a₁₀=17,a₄+a₅+a₆+…a₁₄=77且a_k=13，则k的值等于

(A)16　　　　  (B)18　　　　　 (C)20　　　　  (D)22

4. 若集合S={yy=3^x，x∈R}，T={yy=x²-1，x∈R}，则S∩T是

A.S　　　　　　 B.T　　　　　　  C.φ　　　D.有限集.

5. 过抛物线y²=4x焦点作直线交抛物线于A(x₁,y₁)、B(x₂,y₂)两点，若x₁+x₂=6，则AB等于

 (A)10　　　　  (B)8　　　　　  (C)6　　　　　　 (D)4

6. 已知a_n=(nÎN)，S_n是数列{a_n}的前n项和，则等于

 (A)1　　　　  (B)　　　　  (C)　　　　  (D)

7. 集合A={zz-1≤1,zÎC}, B={zarg(1-z)≥}，在复平面内，A∩B所表示的图形的面积为

　 (A) 　　　　　 (B)　　　　　 (C) 　　　　　 (D)p

8. 函数f(x)=ax³+2(a-1)x²+12(a-2)x+b的图象关于原点对称，则f(x)在[-2,2]上的单调性是

(A)增函数　　　 (B)减函数　　　 (C)在[-2,0]上是增函数，在[0，2]上是减函数
(D)在[-2，0]上是减函数，在[0，2]上是增函数

9. 双曲线 - = 1的两焦点为F₁、F₂，点P在双曲线上，且直线PF₁、PF₂倾斜角之差为，则△PF₁F₂的面积为

（A）16　　　（B）32　　　（C）32　　　（D）42翰林汇

10. 任取x₁，x₂∈[a，b]，且x₁≠x₂，若f()>[f(x₁)+ f(x₂)]，则称是[a，b]上的上凸函数，则下列图象中，是上凸函数的图象的是

　　　　

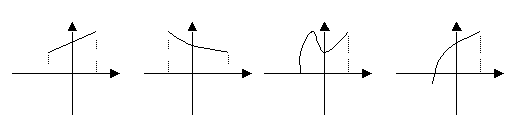
（A）　　　　　 （B）　　　　　　　 （C）　　　　　　  （D）

11. 某种细菌生长很快，长度每天增长一倍，经过20天长度为4m，则生长成要经过

（A）16天　　　　（B）12天　　　（C）10天　　　（D）8天

12. 过圆x²+y²=10x内一点(5，3)有k条弦的长度组成等差数列，且最小弦长为数列的首项a₁，最大弦长为数列的末项a_k，若公差d∈[，]，则k的取值不可能是

（A）4　　　（B）5　　　　（C）6　　　　（D）7

一大题答题卡：

题号	1	2	3	4	5		6	7	8	9	10		11	12
答案

二、填空题：（本大题共4小题，每小题4分，共16分．把答案填在题中横线上．）

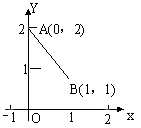13. 根据上海市人大十一届三次会议上的市政府工作报告，1999年上海市完成GDP(GDP是指国内生产总值)4035亿元，2000年上海市GDP预期增长9%，市委、市府提出本市常住人口每年的自然增长率将控制在0.08%，若GDP与人口均按这样的速度增长，则要使本市年人均GDP达到或超过1999年的2倍，至少需　　　 年。（按：1999年本市常住人口总数约1300）

14. 设函数y= f(x)是最小正周期为2的偶函数，它在区间[0，1]上的图象为如图所示的线段，则在区间[1，2]上f(x) =　　　　　　　　 。

15. 在二项式(x-1)¹¹的展开式中，系数最小的项的系数为　　　　　　  　，（结果用数值表示）

16. 定义在R上的偶函数f(x)满足:f(x+1)=-f(x),且在[-1,0]上是增函数，下面是关于f(x)的判断：①f(x)是周期函数；②f(x)的图象关于直线x=1对称；③f(x)在[0,1]上是增函数；④f(x)在[1,2]上是减函数；⑤f(2)=f(0). 其中正确的判断是______________(请把你认为正确的判断都填上)．

三、解答题：（本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．）

17. （1）已知椭圆C的焦点分别为F₁(-2，0)和F₂(2，0)，长轴长为6，设直线y=x+2交椭圆C于A、B两点，求线段AB的中点坐标。

（2）在△ABC中，已知，c=5．求△ABC的内切圆半径．

18. 已知函数f(x)=3x²+bx+1是偶函数，g(x)=5x+c是奇函数，正数数列{a_n}满足a₁=1，f(a_n +a_n－1)-g(a_n+1 a_n+ a_n²)=1，若{a_n}前n项和为S_n，求．

19. 已知等比数列a₁,a₂,a₃,…,a_2n的所有项之和是偶数项之和的3倍，所有项之积为2⁵⁰，且a_n+1=4.　(1)求该数列的项数；　(2)求该数列的通项公式；　(3)设数列{log₂a_n}的前n项和为S_n, 求S_n的最大值．

20. 已知椭圆 + = 1的一条准线是x=2，一倾斜角为的直线交椭圆于A、B两点，且AB的中点坐标为(-1,).  (1)求椭圆的方程；　(2)设P、Q是椭圆上的两点，满足OP、OQ的斜率的乘积k_OP·k_OQ=，求证：OP²+OQ²为定值，并求线段PQ的中点M的轨迹方程．

21. 在XOY平面上有一点列P₁(a₁，b₁)，P₂(a₂，b₂)，P₃(a₃，b₃)，…P_n(a_n，b_n)，…对每个自然数n，点P，位于函数y=2000()²(0<a<10)的图象上，且点P_n，点(n，0)与(n+1，0)构成一个以P_n为顶点的等腰三角形。 （1）求点P_n的纵坐标b_n的表达式。　（2）若对每个自然数n，以b_n，b_n+1，b_n+2为边长能构成一个三角形，求a取值范围。　（3）设B_n= b₁ b₂ b₃…b_n(n∈N)，若A取（2）中确定的范围内的最小整数，求数列{B_n}的最大项的项数。

22. 已知复数z₀=1-mi(m>0)，z=x+yi和w=x¹+y¹i，其中x，y，x¹，y¹均为实数，i为虚数单位，且对于任意复数z，有w=，w=2z.　（1）试求m的值，并分别写出x¹和y¹用x、y表示的关系式；　（2）将(x、x)作为点P的坐标，(x¹、y¹)作为点Q的坐标，上述关系可以看作是坐标平面上点的一个变换：它将平面上的点变到这一平面上的点Q，当点P在直线y=x+1上移动时，试求点P经该变换后得到的点Q的轨迹方程；　（3）是否存在这样的直线：它上面的任一点经上述变换后得到的点仍在该直线上？若存在，试求出所有这些直线；若不存在，则说明理由。