十六、抽屉原则
训练A卷
班级______姓名______得分______
1.画图说明,把4支铅笔放入3个笔盒内,共有______种不同的放法,各种放法中总有______个笔盒内铅笔的支数不少于2支。那么把n+1件物品放入n个抽屉内,总有一个抽屉内的物品不少于______件。
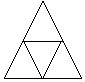
2.把 5个棋子放入下图中四个每条边长为“1”的小三角形内,那么一定有一个小三角形内至少有______个棋子,两棋子的距离一定小于______。
3.在一条1米长的线段上的任意六个点,试证明这六个点中至少有两个点的距离不大于20厘米。
4.学校举行开学典礼,要沿操场的400米跑道插40面彩旗,试证明不管怎样插至少有两面彩旗之间的距离不大于10米。
5.跳绳练习中,一分钟至少跳多少次才能保证某一秒钟内至少跳了两次?
6.一只鱼缸有很多条鱼共有五个品种,问至少捞出多少条鱼,才能保证有五条相同品种的鱼?
7.有甲、乙两种不同的书各若干本,每个同学至少借一本,至多借二本,(同样的书最多借一本)只要有几个同学借书,就可保证有两人借的书完全相同。
8.篮子里有苹果、梨、桃子和桔子,如果每个小朋友都从中任意拿两个水果,问至少有多少个小朋友才能保证至少有两个小朋友拿的水果完全一样?
9.六个小朋友每人至少有一本书,一共有20本书,试证明至少有两个小朋友有相同数量的书。
10.用红、黄两种颜色将2×5的矩形的小方格随意涂色,每个小方格涂一种颜色,证明必有两列它们的小方格中涂的颜色完全相同。
11.10双不同尺码的鞋子堆在一起,若随意地取出鞋来,并使其至少有两只鞋可以配成一双,试问需取出多少双鞋就能保证成功?
12.某次会议有10位代表参加,每位代表至少认识其余9位中的一位,试说明这10位代表中,至少有2位认识人的个数相同?
13.布袋中装有塑料数字1、2、3各若干个,每次任选6个数字相加,至少选多少次才能保证有两个相加的和相等。
训练B卷
班级______姓名______得分______
1.将7支铅笔放入2个笔盒内,共有______种放法,各种放法中总有一个笔盒内铅笔支数不少于______支,因为7=______×2+1。一般来说,把k×n+1件物品放入n个抽屉内,一定有一个抽屉内物品不少于______+1件。
2.把9个点放入边长为1的2×2的小方格内,那么至少有一个小方格内有______个点,并且这一格内的点组成图形的面积一定小于______。
3.夏令营有400个小朋友参加,问在这些小朋友中:
(1)至少有多少人在同一天过生日?
(2)至少有多少人单独过生日?
(3)至少有多少人不单独过生日?
4.在一副扑克牌中,最少要拿多少张,才能保证四种花色都有。
5.证明在任意的37人中,至少有4人的属相相同。
6.一个正方体有六个面,给每个面都涂上红色或白色,证明至少有三个面是同色。
7.学校开办了语文、数学、美术和音乐四个课外学习班,每个学生最多可以参加两个(可以不参加)。至少在多少个学生中,才能保证有两个或两个以上的同学参加学习班的情况完全相同。
8.在边长为1的三角形中,任意放入5个点,证明其中至少有两个点之间的距离小于1/2。
9.证明:任意取12个自然数,至少有两个自然数被11除的余数相同。
10.至少要给出多少个自然数(这些数可以随便写),就能保证其中必有两个数,它们的差是7的倍数。
11.有甲、乙两种不同的书若干本,每个同学至少借1本,至多借2本(同样的书不能借2本),需要多少个同学借书,就可保证其中有10个借的书完全相同?
12.用红、蓝两种颜色将一个 3 × 9的矩形小方格随意涂色,证明:必有两列,它们的小方格中涂的颜色完全相同。

13.从1、2、3、4、5、6、7、8、9、10这10个数中,任意取出6个数,证明,从中至少能找出两个数,其中一个数是另一个数的整数倍。
14.任取10个整数,证明其中至少有两个数的差能被9整除。
15.任意给定的五个整数中,必有三个数的和是3的倍数。
训练C卷
班级______姓名______得分______
1.口袋中有三种颜色的筷子各10根,问:
(1)至少取多少根才能保证三种颜色的筷子都取到?
(2)至少取多少根才能保证有两双不同颜色的筷子?
(3)至少取多少根才能保证有两双颜色相同的筷子?
2.为了丰富暑假生活,学校组织甲、乙两班进行了一次军棋对抗赛,每班各出五人,同时对奕。比赛时天气很热,学校给选手们准备了两种饮料,有可乐,有汽水,每个选手都选用了一种饮料,证明至少有两对选手,不但甲班选手用的饮料相同,而且乙班选手用的饮料也相同。
3.100名少先队员选大队长,候选人是甲、乙、丙三人,选举时每人只能投票选举一人,得票最多的人当选,开票中途累计,前61张选票中,甲得35票,乙得10票,丙得16票。问在尚未统计的选票中,甲至少再得多少票就一定当选?
4.证明:在从1开始的前10个奇数中任取6个,一定有两个数的和为20。
5.任意写一个由数字1、2、3组成的三十位数,从这三十位数中任意截取相邻三位,可得一个三位数,证明从所有不同位置中任意截取的三位数中至少有两个相同。
6.在一个半径为1的圆内,随意放置7个点,证明必有两个点之间距离不超过1。
7.证明:从1、2、3……、19、20这二十个数中,任选12个不同的数,证明其中一定包括两个数,它们的差是10,也一定包括两个数,其差是11。
8.把1到10,这10个自然数摆成一个圆圈,证明一定存在相邻的三个数,它们的和大于 17。
9.从自然数1,2,3,4,……,99,100中,任意取出51个数,求证其中一定有两个数,它们中的某一个数是另一个数的倍数。
10.任意给定的七个不同的自然数,求证其中必有两个数,其和或差是10的倍数。
11.把1到100这100个自然数中,任意取出51个,证明其中必定能找出2个数,它们的差等于50。
12.设x1、x2、……x30是任意给定的30个整数,证明其中一定存在8个整数,把这8个整数用适当的运算符号连接起来,结果正好是1155的倍数。
DAAN
A卷
1.3,1,2
2.2,1
3.将一米长的线段等分成五段,每段20厘米长,作为五个抽屉,按照抽屉原理,一定有一段里有两个点,它们间距离小于20厘米。
4.将跑道分成10米一段,共40段
5.61
6. 21 因为考虑到最坏的情况即捞了20条出现每种4条,捞了第21条一定出现一种鱼有5条。
7.4 因为借一本有两种情况,借二本只有一种情况,将三种情况作为三个抽屉
8.11 四种水果我们用甲、乙、丙、丁表示,拿二个水果情况有如下10种情况:(甲、甲),(乙,乙),(丙,丙),(丁,丁),(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁)
9.因为每人不同的话,那就要有1+2+3+4+5+6=21本,现在只有20本,说明某一人缺一本,此人一定出现出2,3,4,5,6里,所以一定有两个小朋友的数量是相等的。
10.因为用两种颜色涂2×1小方格出现如下四种情况(红红),(黄黄),(红黄),(黄红)
11.11
12.因为认识人数分:1人,2人,……9人,9种情况,这九种情况作为9个抽屉
13.14次 提示数字1,2,3任选六个组成和是从6,7……18共13种情况
B卷
1.4,4,7=3×2+1,1
2.2,1
3.2,0,35
4.42,因为有2张花牌
5.因为属相有12种,而37=3×12+1所以有4人属相相同。
6.以红,白二色为抽屉,而6=3×2,所以至少有三面同色
7.12人 本题同学参加情况共11种,(不参加)(语),(数),(美),(音乐),(语,数),(语,美),(语,音),(数,美),(数,音),(美,音)
![]() 角形为抽屉
角形为抽屉
9.因为11为除数,余数有0、1、2……10,共11种情况,所以12个自然数被11除至少有两个数的余数相同。
10.8,方法同第9题,因为余数相同的两数之差一定能被除数整除。
11.28人,因为借书情况分三类,(甲),(乙),(甲,乙)
所以k×3+1中要k+1=10,k=9,所以总人数为9×3+1=28
12.因为涂色出现八种情况(红红红),(蓝,蓝,蓝),(红,红,蓝),(红,蓝,红),(蓝,红,红),(蓝,蓝,红),(蓝,红,蓝),(红,蓝,蓝),所以九列中一定有两列是相同的。
13.本题设计如下五个抽屈:(1,7),(6,2),(9,3),(8,4),(10,5)
14.仿题9
15.按照被3除所得的余数,即构成三个抽屉,如果5个数中有三个在同一抽屉内,余数的三倍能被3整除,如果每一个抽屉最多只有二个数,那么此时各抽屉里都有,就各抽屉里取一个,它们的余数和为0+1+2=3能被3整除。
C卷
1.(1)21
(2)13
(3)10
2.因为每对选手用饮料有四种情况:(可,可),(汽,汽),(可,汽),(汽,可),用这四种情况作为四个抽屉来解决
3.11
4.构造如下五个抽屉解决:(1,19),(3,17),(5,15),(7,13),(9,11)
5.因为可以截成28节,而用1,2,3组成的三位数有27种(数字可重复)
6.将圆分成如图所示的6份,至少有一份中有2点逐一加以讨论。
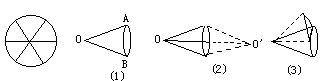
7.构造如下的抽屉:
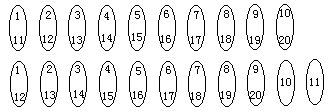
8.将相邻三个数为一个抽屉,这10个抽屉里的数的总和为:1+2+3+2+3+4+3+4+5+……+10+1+2=3×(1+2+3+4+5+6+7+8+9+10)=165=16×10+5用抽屉原理二解决16+1=17
9.本题构造如下50个抽屉:
1, 1×2,1×22, 1×23, 1×24,1×25,1×26
3,3×2,3×22,3×23,3×24,3×25
5,5×2,5×22,5×23,5×24
7,7×2,7×22,7×23
9,9×2,9×22,9×23
11,11×2,11×22,11×23
13,13×2,13×22
15,15×2,15×22
17,17×2,17×22
19,19×2,19×22
21,21×2,21×22
23,23×2,23×22
25,25×2,25×22
27,27×2
29,29×2
49,49×2
51,
53
…
99
10.构造如下6个抽屉,(放个位数为0),(放个位数为13×9)(放个位数为2或8),(放个位数为3或7),(放个位数为4或6)(放个位数为5),显然每个抽屉中的任意两个数和或差是10的倍数
11.构造如下50个抽屉:(1,51),(2,52),(3,53)……(50,100)
12.∵1155=3×5×7×11将30个数分成四组
第一组4个数 能找出二数之差是3的倍数
第二组6个数,能找出二数之差是5的倍数
第三组8个数,能找出二数之差是7的倍数
第四组12个数,能找出二数之差是11的倍数
然后这四个差连乘起来。
