梯形面积的计算

教学目标：

1．　理解梯形面积公式的推导过程，会应用公式正确计算梯形的面积。

2．　培养学生合作的能力。

3．　继续渗透旋转、平移的能力。

教学重点：

理解并掌握梯形面积公式的计算方法。

教学难点：

理解梯形面积公式的推导过程。

教学过程：

一、复习旧知

（一）求出下面图形的面积

　　　　 

　　　　　　　　　　

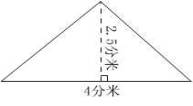
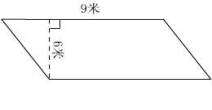
（二）回忆三角形面积公式的推导过程（演示课件：拼摆三角形）

（三）学生讨论：在日常生活中你见过哪些物品是梯形的？

二、设疑引入

车窗的玻璃是梯形的，你能用学过的方法推导出梯形的面积公式吗？

板书课题：梯形的面积

三、指导探索

（一）梯形面积公式的推导。

1．小组合作操作讨论

（1）用两个完全一样的梯形可以拼成一个　　　　　　 形。

（2）这个平行四边形的底等于　　　　　　  ；高等于　　　　　　 。

（3）每一个梯形的面积等于平行四边形面积的　　　　　　  。

（4）梯形的面积等于　　　　　　　 。

2．小组汇报（拼摆教具，叙述推导梯形面积公式的过程）

3．学生概括总结，归纳公式

教师提问：

（1）要求梯形的面积必须知道什么条件？

（2）（上底+下底）×高求的是什么？

（3）为什么要除以2？

教师板书：

梯形面积=（上底+下底）×高÷2

S= ( a + b )×h÷2

(二)教学例1。

例3：我国三峡水电站大坝的横截面的一部分是梯形（如下图），求它的面积。

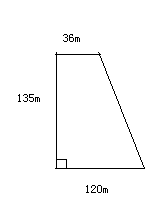
1．　教师提问：已知什么？求什么？怎样解答？

2．　列式解答：　　 S = ( a + b ) h÷2

　　　　　　　　　  =(36+120)×135÷2

　　　　　　　　　  =156×135÷2

　　　　　　　　　　=10530(平方米)

答：它的面积是10530平方米。

四、巩固练习

（一）课本P89,做一做。

（二）计算下面梯形的面积

　　 　　　　

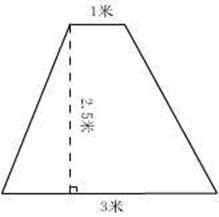
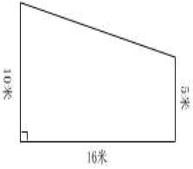
（二）动手测量学具（梯形）的相关数据，并计算梯形学具的面积。

（三）下面是一个水电站拦河坝的横截面图，求它的面积。

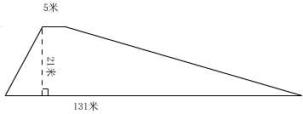
五、质疑总结

师生共同回忆这节课学习的内容。

教师提问：求梯形的面积为什么要除以2？求梯形面积需要知道哪些条件？

（二）引导学生质疑，指导学生解题。

六、板书设计

梯形的面积

梯形的面积=（上底+下底）×高÷2　　　　　　　 S=( a ＋ b ) h÷2

S=( a ＋ b ) h÷2　　　　　　　　　　  =( 36 ＋ 120 ) 135÷2

　　　　　　　　　　　　　　　　　　  =156×135÷2

　　　　　　　　　　　　　　　　　　  =10530(平方米)

　　　　　　　　　　　　　　　　　　 答：它的面积是10530平方米。