空间与图形试题

一、填空题。

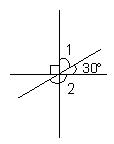
　　1，下左图中，∠1=（　　）°，∠2=（　　）°。

　　 　　　　　 

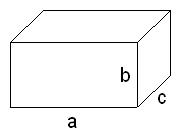
　　2，观察上右图，在括号内填字母，使等式成立。

　　　

　3，用圆规画图，当圆规两脚之间的距离为（　　）厘米时可以画出直径为2厘米的圆，这个圆的面积是（　　）平方厘米。

　　4，一张正方形纸的边长为，从这张纸上剪下一个边长为（＞）的小正方形，用字母表示剩余部分的面积是（　　　　）。

　　5，一个平行四边形的底是5分米，面积是120平方分米，高是（　　）分米，与它等底等高的三角形面积是（　　）平方分米。

　　6，如下图（单位：厘米），三角形的面积是（　　）平方厘米，平行四边形与梯形的面积的最简整数比是（　　　　）。

　　　　　 

　7，把下边的长方形以15厘米长的边为轴旋转一周，会得到一个（　　　），它的表面积是（　　　）平方厘米，体积是（　　　）立方厘米。

　　　　　　　　

　　8，求一个圆柱形铁桶的占地面积是求它的（　　　），求做这个铁桶需要多少铁皮，是求它的（　　　）。

9，用两个相同的正方体木块拼成一个长方体，长方体的表面积比两个正方体的表面积的和少16平方厘米，一个正方体的表面积是（　　　）平方厘米。

　　10，下面形体是由棱长为1厘米的小正方体搭拼成的，它的表面积是（　　　）平方厘米；至少还需要（　　）个这样的小正方体，才能搭拼成一个正方体。

　　　　　　 

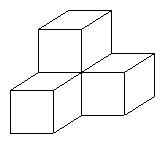
　　11，如下图所示，用棱长分别是1米、2米的两个正方体组成一个物体，那么这个物体的表面积是（　　　）平方米。

　　　

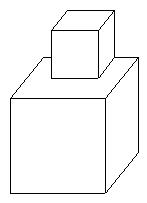
　　12，用边长为1分米的小正方体，拼成一个较大的正方体，至少需要（　　）个这样的小正方体，把这些小正方体排成一行，它的长度是（　　）分米。

　13，把24分米长的铁丝折成一个最大的正方形，它的面积是（　　）平方分米，如果把这根铁丝折成一个最大的正方体，它的体积是（　　）立方分米。

　14，一种圆柱形铁皮油桶的底面直径是40厘米，高是50厘米，这个油桶的容积是（　　　）毫升。

　　15，一个圆柱体和一个圆锥体的体积相等，它们底面积的比是3：5，圆柱的高是8厘米，圆锥的高是（　　）厘米。

二、判断题。

　　1，两条不相交的直线叫做平行线。　　　　　　 （　　）

2，经过平面上的一点可以画无数条直线，经过平面上的两点只能画一条直线。　　　　　　　　　　　　　　　　 （　　）

3，因为三角形不易变形，所以房子的梁架做成三角形形状。（　　）

4，三角形中最大的角不小于60度。　　　　　  （　　）

5，将一张正方形纸连续对折三次，展开后其中一份是这张纸的。（　  ）

6，所有的三角形都是轴对称图形。　　　　　　　  （　　）

7，左图是一个轴对称图形。　　　（　　）

8，圆的周长是它的直径的3.14倍。　　　　　　 （　　）

9，压路机滚筒在地上滚动一周所压的路面正好是压路机滚筒的表面积。　　 　　　　　　　　　　　　　　　　　 （　　）

10，圆锥的体积比与它等底等高的圆柱的体积小。　（　　）

三、选择题。

1，三角形中最小的一个角是50°，按角分类这是一个（　　）三角形。

A、锐角　　B、直角　　C、钝角　　D、不能确定

2，用一根木条给一个长方形加固，若只考虑加固效果的话，采用（　　）最好。

　

3，下图能画（　　）条对称轴。

　　　　　　

　　A、2条　　B、4条　　C、8条

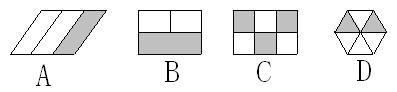
4，下面图形中，哪些图形的阴影部分占整个图形的。（　　）

　　

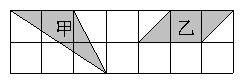
5，下图中，甲和乙两部分面积的关系是（　　）。

　　

6，如果一个圆的面积100，那么它的周长是（　　）。

　 A、10　  B、10　　C、20　  D、100

7，如下图，两个完全一样的直角三角形重叠一部分，图中阴影部分面积是（　　）平方厘米。

　　

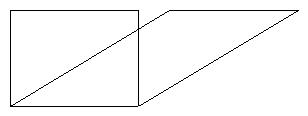
8，下图中长方形面积（　　）平行四边形面积。

　　

9，用一条长16厘米的铁丝围成一个长方形，如果长和宽都是质数，它的面积是（　　）平方厘米。

　A、6　　B、10　　C、15　　D、21

10，两个完全相同的长方形（如下图），将图①和图②阴影部分的面积相比，（　　）。

　　

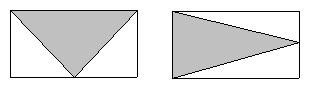
　　　　  图①　　　　　　　图

　A、图①大　　B、图②大　　C、图①与图②相等

11，一个圆的半径扩大3倍，这个圆的面积就扩大（　　）倍。

　　A、3　　B、6　　C、9

12，正方形与圆的面积相等，那么正方形的周长（　　）圆的周长。

　　A、等于　　B、小于　　C、大于

13，一个圆柱体的侧面展开图是一个正方形。这个圆柱底面直径与高的比是（　　）。

　　A、1：　　B、1：2　  C、1：4　  D、2：

14，两张完全相同的长方形纸片，一张以它的长作底面周长，另一张以它的宽作底面周长，分别卷成圆柱形（接口处不重叠），再装上底面，所得两个圆柱体的（　　）一定相等。

　　A、表面积　　B、体积　　C、侧面积

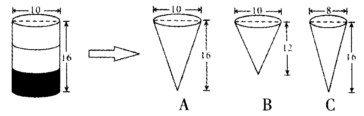
15，圆柱内的沙子占圆柱的，倒入（　　）内正好倒满。

　　

四、画图与计算。

1，（1）在下图中，画出表示A点到直线距离的线段。

　　　　　　　　 

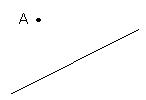
（2）过A点作已知直线的平行线。

（3）量一量，A点到已知直线的距离是（　　）厘米。

2，以小明家为观测点，根据下面条件在平面上标出各地的位置。

　　　　　　

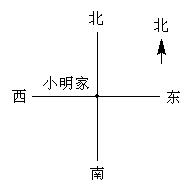
（1）学校在小明家北偏东70°的方向上，距离小明家2千米处。

（2）书店在小明家西偏南60°的方向上，距离小明家3千米处。

3，学校有一块长方形的试验田，长90米，宽60米。请你用1：2000的比例尺画出这块试验田的平面图。（先算一算，这块试验田的长和宽各应画多长，再画出来）

4，下面是用1：4000的比例尺画出的一块水稻试验田的平面图。请你：

　　

（1）量一量：它的上底是（　　）厘米，下底是（　　）厘米。（取整厘米数）

（2）算一算：它的实际面积是（　　）公顷。

（3）画一画：以上图的高为直径画一个圆。

（4）算一算：你画的这个圆的面积是（　　　）平方厘米。

5，某市区主要街道分布情况如下图。

　　　　

先动手测量你认为有用的数据（取整厘米数），再解决以下问题：

（1）文明路长1800米，这幅图的比例尺是多少？

（2）光明路在幸福大街的南边正东方向，请你画在图上，并标出来。

6，

五、周长与面积计算。

1，求图中阴影部分的面积。（单位：厘米）

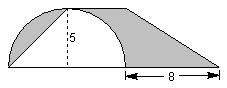
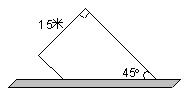
2，张大爷用篱笆围一块梯形菜地，一面靠墙（如下图）。篱笆全长48米，如果每平方米收白菜9.5千克，这块地一共可以收白菜多少千克？

3，学校有一块长方形空地，长50米，宽20米，要在这块空地内留出的面积进行绿化。在绿化面积内用的面积种植花卉，在剩余的面积内规划一个最大的三角形种植草坪。请你设计一下，并画出草图。（比例尺 1：1000）

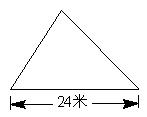
4，公园里有一块面积是180平方米的三角形绿地（如下图），底长24米。绿地扩展，把底延长8米，高不变。

（1）请在下图上画出扩展后的三角形绿地。（只需画出示意图）

（2）列式计算出扩展后三角形绿地的总面积。

　　　　　　　　

5，某小区物业要在社区内活动室门前修一个圆形花坛，已知花坛的周长是37.68米。

（1）这个圆形花坛的面积是（　　　）平方米。

（2）请用1：400的比例尺把这个圆形花坛的平面图画出来（标明圆心和半径），图中花坛的半径是（　　）厘米。

六、表面积与体积的计算。

1，求空心机器零件的体积。（单位：厘米）

　　

2，在一个长、宽、高分别是2分米、2分米、5分米的长方体盒子中，正好能放下一个圆柱形物体（如下图）。这个圆柱形物体的体积最大是多少立方分米？盒子中空余的空间是多少立方分米？

　　　　　

3，学校要捐赠一批教学物资给希望小学，其中有24盒粉笔，每盒都是棱长1分米的正方体包装。

（1）请你设计一个长方体包装箱来装这些粉笔。

你设计的包装箱内尺寸是：长（　　　），宽（　　　），高（　　　）。

（2）计算你设计的包装箱至少需要多少纸？（接头处忽略不计）

4，一种液体饮料采用长方体塑封纸盒密封包装。从外面量盒子长6厘米，宽4厘米，高10厘米。盒面注明“净含量：240毫升”。请分析该项说明是否存在虚假。

5，2006年炎热夏天到来之前，有一位好心人准备捐资建一座标准化的游泳池，这个游泳池的长是60米，宽是长的。

（1）这个游泳池的占地面积是多少平方米？

（2）挖成这个游泳池共挖土多少立方米？

（3）在池的侧面和池底抹一层水泥，抹水泥的面积是多少平方米？

6，要制作一个无盖圆柱形水桶，有以下几种型号的铁皮可以供搭配选择。（单位：分米）

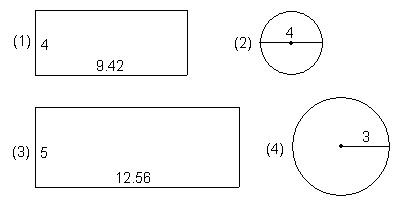
（1）你选择的材料是（　　）号。

（2）你选择的材料制成水桶的容积是多少升？

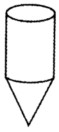
7，一种儿童玩具——陀螺（如下图），上面是圆柱体，下面是圆锥体。经过测试，只有当圆柱直径3厘米，高4厘米，圆锥的高是圆柱高的时，才能旋转时稳又快，试问这个陀螺的体积是多大？（保留整立方厘米）

　　　　　

七、能力发展题。

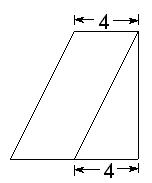
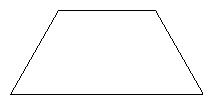
1，一个等腰梯形的下底是上底的2倍，把它分成4个面积相等，形状相同的梯形，请动手试一试。

　　　

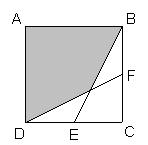
2，下图是一个正方形，边长6厘米，E、F分别是CD、BC的中点，求阴影部分的面积。

　　　　

3，下图是两个完全一样的等边三角形，在三角形内有一点A。

　　　　　

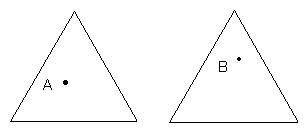
（1）由点A向三角形的三条边作出三条垂线，并且量出三条垂线的总长是多少。

（2）在三角形内再任选一点B，向三角形的三条边作出三条垂线，并且量出三条垂线的总长。看看你能发现什么，把你的发现写下来。

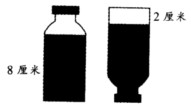
4，巧求胶水的体积。

一个胶水瓶（如下图），它的瓶身呈圆柱形（不包括瓶颈），容积为32.4立方厘米。当瓶子正放时，瓶内胶水液面高为8厘米，瓶子倒放时，空余部分高为2厘米。请你算一算，瓶内胶水的体积是多少立方厘米？