期末复习（下学期） 期末达优检测

 

（时间:90分钟 分数：120分）

1.填空。（24分）

（1）一个五位数，十位上的数字是最小的合数，百位上的数字是最小的质数，千位上的数字是最小的自然数.如果这个数能被2和5整除，这个数最小的是（　　）。

（2）把化成循环小数，用循环节表示是（　　 ）。

（3）甲数是a，比乙数的少b，表示乙数的式子是（　　　）。

（4）甲数是50，乙数是20，甲数比乙数多（　　）％，乙数比甲数少（　　 ）％。

（5）一个数，如果将它的小数点向左移动一位，那么所得的新数比原数少6.3，原数是（　　）。

（6）从8点45分到9点9分，分针旋转的角度是（　　）。

（7）1的分子加上27，要使这个分数的大小不变，分母应加上（　　　　）。

　　（8）把2、2.65％、2.6、2.按照从小到大的顺序排列是（　　　）＜（　　 ）＜（　　 ）＜（　　 ）。

（9）某村粮食作物播种面积减少，要保持粮食总产量不变，每公顷产量需增加（　　 ）％。

（1O）一个长方形，如果它的长和宽都增加4厘米，所形成的新长方形面积比原来长方形面积大112平方厘米，原来长方形的周长是（　　）厘米。

（11）两数相除，商3余4，如果把被除数、除数、商及余数相加，和是43，被除数是（　　）。

（12）一个圆柱体的侧面积是942平方厘米，体积是2355立方厘米，它的底面积是（　　）平方厘米。

2.判断。（对的打“√”，错的打“×”）（5分）

（1）两条直线如果永不相交，这两条直线一定互相平行。（　　）

（2）自然数除了质数，其余都是合数。（　　）

（3）甲数的等于乙数的，那么甲数一定比乙数小。（　　 ）

（4）圆的半径和它的周长成正比例。（　　）

（5）三角形的底一定，底边上的高和面积成正比例。（　　）

3.选择正确答案填在括号里。（5分）

　　（1）如果ab＝0，那么（　　 ）。

①a和b都等于0　 　　 ②a和b至多有一个是0　　 ③a和b至少有一个是0

（2）甲、乙两人各走一段路，他们所用的时间的比是4：5，速度的比是5：3，他们走的路程的比是（　　　）。

①4：3　　　　　　　②12：25　　　　　　③不能确定

（3）数a精确到0.01时近似值是2.90，那么a的取值范围是（　　）。

①2.80≤a＜3.00　　　　②2.85≤a＜2.65　　　　　 ③2.895≤a＜2.905

（4）如果甲数比乙数大10％，而乙数比丙数小10％，那么甲、丙两数的大小关系是（　　）。

①甲=丙　　　　　　 ②甲＞丙　　　　　　③甲＜丙

（5）圆柱体与圆锥体的底面积相等，圆柱体的高是圆锥体的高的，则圆锥体的体积是圆柱体体积的（　　　）。

①　　　　　　 ②3倍　　　　　　　③2倍

4.计算。（31分）

（1）直接写出得数。

5--=　　　　　　　 +-+=

÷×5=　　　　　　　　777×9+111×37=

72÷1.2+72÷1.8=　　　　 9+3÷7÷6×14=

+++=　　　　　　8.4×13-3×8.4=

60×（1--）=　　　　　×996=

（2）求未知数x。

÷x=　　　　　　　 -14.5=5.5

 

 

（3）脱式计算。

1.26÷0.4÷31.5　　　　　　 -（+）+

 

 

（+）×（-）　　　　　　[34-（+）×30]÷

 

 

（1-）÷[（0.1+1.1）÷0.2]

 

 

5.求阴影部分面积。（单位：厘米）（5分）

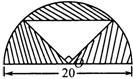
6.应用题。（30分）

（1）一批煤用去25％，还剩48吨。这批煤共有多少吨。

 

 

（2）甲、乙两列火车分别从两城同时相向开出，在甲车比乙车少走36千米时，两车还相距264千米。已知甲、乙两车速度的比为5：6，求这两城相距多少千米。

 

 

（3）蓝天服装厂3月份计划加工女西服5400件，结果上半月完成了，下半月完成了，这个月比原计划多加工女西服多少件？

 

 

（4）甲、乙两地相距504千米，一辆汽车从甲地开往乙地用6小时行了全程的。照这样的速度，几小时到达？

 

 

（5）师徒二人分别接受同样多零件的生产任务。他们各工作16天后，师傅还需生产64个，徒弟还需生产384个，才能完成各自的任务。已知徒弟的工作效率比师傅少40％，师傅每天生产多少个零件？

 

 

附加题。（20分）

　　（1）某工厂第一车间的人数比第二车间人数的少30人，如果从第二车间调10人到第一车间，这时第一车间的人数是第二车间人数的，第二车间原来有多少人？

 

 

（2）客车与货车同时从甲、乙两镇的中点，向相反方向行驶，3小时后，客车到达甲镇，货车离乙镇还有30千米。已知货车速度是客车的，甲、乙两镇相距多少千米？

 

 

 

参考答案

1.（1）11240　（2）0.8　（3）（a+b）　（4）150%,60%。　（5）7　（6）144　（7）21　（8）2.65%＜2.65＜2.＜2（9）25%　（10）48　（11）28　（12）78.5

2.（1）×　（2）×　（3）√　（4）√　（5）√

3.（1）a和b至少有一个是0　　（2）12:25　（3）2.895≤a＜2.905　（4）甲＜丙　（5）2倍

4.（1）4　1　15　11100　100　10　1　84　10　994

（2）x=　x=160　（3）0.1　　　30　

5.3.14×（）²×-（）²×=107（平方厘米）

6.（1）48÷（1-25%）=64（吨）

（2）分析:在相同的时间内:速度的比等路程的比,设乙车走了x千米,则甲车走了（x-36）千米。

=　（x=216）

216×2-36+264=660（千米）

（3）方法一:5400×（+）-5400=1200（件）

方法二:5400×（+-1）=1200（件）

（4）方法一:1÷（÷6）=8（小时）

方法二:（540×）÷6=67.5（千米/时）

540÷67.5=8（小时）

（5）设师傅每天生产x个零件,则徒弟每天生产（1-40%）x个

16x+64=（1-40%）x×16+384

x=50

附加题

（1）设第二车间原有x人,则第一车间原有（x-30）人

（x-10）= x-30+10

　 x=250

（2）分析:相同的时间内,路程的比=速度的比

30÷（1-）×2=240（千米）