模拟试卷30
一、填空题:
![]()
![]()
3.37□5□能被72整除,这个数除以72的商是______.
4.一列火车以每小时60千米的速度通过一座200米长的桥,用了21秒,则火车的车长是______米. 
![]()
7.有两支蜡烛,第一支5小时燃尽,第二支4小时燃尽.如果同时点燃这两支蜡烛,并且蜡烛燃烧的速度不变,在点燃______小时后,第一支蜡烛的长度是第二支蜡烛的3倍.
![]()
9.恰有8个约数的两位数有______个.
10.某小学组织六年级学生春游,学校买了182瓶汽水分给每个学生.如果每5个空瓶又可换得1瓶汽水,那么这些汽水瓶最多可换得______瓶汽水.
二、解答题:
1.如果1个小正方体木块的表面积是24平方厘米,那么由512个这样的小正方体木块所组成的一个大正方体的体积是多少立方厘米?

3.有6对夫妻参加一次聚会,每个男士与每一个人握手(但不包括自己的妻子),女士之间相互不握手,那么这12个人共握手多少次?
4.甲、乙、丙三人同时从A地出发,到离A地F18千米的B地,当甲到达B地时,乙、丙两人离B地分别还有3千米和4千米,那么当乙到达B地时,丙离B地还有多少千米?
模拟试卷30
一、填空题:
![]()
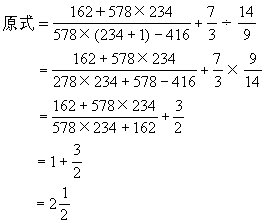
2.余2
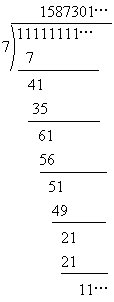
连续6个1能被7整除,说明每6个1除以7是一个循环.由于
1997÷6=332…5
这表明1997个1除以7的余数等于5个1除以7的余数,因为5个1除以7余数是2,所以1997个1除以7余数是2.
3.523
因为72=8×9,8与9互质,所以这个五位数既是9的倍数,又是8的倍数.
由于这个五位数是9的倍数,所以其各个数位上的数字之和应是9的倍数,不妨设五位数的个位是x,百位是y,则
3+7+y+5+x=15+y+x
是9的倍数,所以x+y可能是3或12;
若x+y=3,3=1+2,由于这个五位数又能被8整除,因此这个五位数的末三位数字组成的数能被8整除,且个位必是偶数,但152不能被8整除,所以x+y不可能是3.
若x+y=12,12=4+8=6+6,但458,854均不能被8整除,只有656能![]()
这个五位数除以72的商是523.
4.150米
火车通过一座桥是指火车头在桥一端算起到火车尾在桥的另一端为止.因此火车通过一座桥所行的路程实际是桥长加上火车的车长.并且计算时注意换算单位要一致,这样可以求出火车的车长是:
60×1000÷3600×21-200
![]()
=350-200
=150(米).
5.10平方厘米
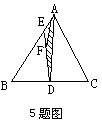
根据等底等高的三角形面积相等,由于D是BC的中点,△ABD的面积等于△ADC的面积,有
S△ABD=S△ADC=120÷2=60(平方厘米)
![]()
S△AED=S△ABD=60÷4=15(平方厘米)
![]()
![]()
6.末尾有3996个0.
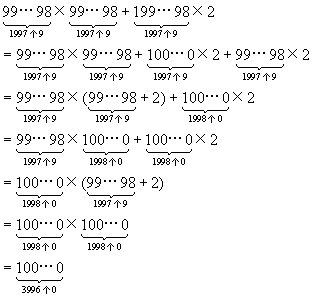
7.3.5小时
把两支蜡烛燃烧的速度看作每小时燃烧1个单位长,则第一支蜡烛长为5个单位长,第二支蜡烛长为4个单位长.
设点燃x小时后,第一支蜡烛是第二支蜡烛的长度的3倍,列方程为:
5-x=3(4-x)
5-x=12-x
2x=7
x=3.5(小时)
![]()
先求出这499个数的和,然后求出这499个数中的所有整数之和,它们的差即为所求,所以
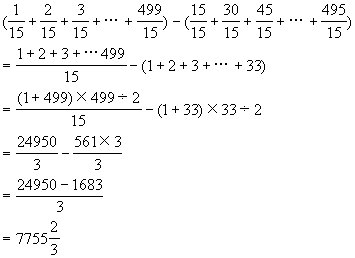
9. 10个
因为8=1×8=2×4=2×2×2,根据约数与质因数的关系知,含有8个约数的数N可以表示成:N=a7或N=a×b3或N=a×b×c
其中a、b、c是N的质因数.下面采用枚举法得:
N=27=128,超过两位数,舍去;
N=2×33=54, N=3×23=24, N=5×23=40,
N=7×23=56, N=11×23=88,
N=2×3×5=30,N=2×3×7=42,N=2×3×11=66,
N=2×3×13=78,N=2×5×7=70恰有8个约数的两位数有10个.
10. 45瓶
先用182个空瓶可换得汽水是:
182÷5=36…2
36瓶,还余2个空瓶.喝完这36瓶汽水连同余下的2个空瓶,又可换得汽水是
(36+2)÷5=7…37瓶,还余3个空瓶.再喝完这7瓶汽水连同余下的3个空瓶,又可换得汽水是:
(7+3)÷5=22瓶,所以这些汽水瓶最多可换得汽水:
36+ 7+ 2= 45(瓶).
二、解答题:
1. 4096立方厘米.
小正方体的每个面的面积是:
24÷6= 4(平方厘米)
小正方体的棱长是2厘米,由于
512= 8×8×8
所以大正方体的棱长为8个小正方体的棱长,因此大正方体的棱长是:
2×8=16(厘米)
大正方体的体积是:
16×16×16=4096(立方厘米).
2.45(人)
订《儿童故事画报》的人数是:
订《好儿童》的人数是:
![]()
两种都订的人数是:
![]()
81+72-108=45(人).
3.45次
由于女士之间相互不握手,因此这12个人握手的情况分为两类:一类是男士之间相互握手,另一类是男士与女士握手,但每个男士不与自己的妻子握手.
6个男士之间两两握手,每个男士与其余5个男士握手一次,共握手 5× 6= 30次,但这 30次握手有重复计算,如甲、乙两个握手,把甲与乙握手和乙与甲握手算成两次不同的握手,所以6个男士相互握手,共握手:
5×6÷2=15(次)
男士与女士握手的情况共有:
6×5=30(次)
所以这12个人共握手:
15+30=45(次)
![]()
当甲行了18千米时,乙行了18-3=15千米,丙行了18-4=14千米,甲、![]()
![]()
![]()