模拟试卷31
一、填空题:
![]()
2.有20个约数的最小自然数是______.
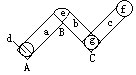
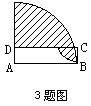
3.如图,AB=6厘米,BC=2厘米,ABCD是长方形,则阴影部分的面积是______平方厘米.
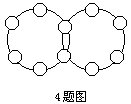
4.把1,2,7,8,9,10,12,13,14,15填入图中的小圆内,使每个大圆圈上的六个数的和是60.
![]()
6.体操选手的选拔赛上,每名裁判员给选手的最高分不超过10分.某位选手的得分情况如下:全体裁判员给的分数的平均分是9.72分,如果去掉一个最低分,则其余裁判员给的分数的平均数是9.76分,如果去掉一个最高分,则其余裁判给的分数的平均数是9.68分.那么所有裁判员给的分数中最低分至少是______分,共有______名裁判员.
7.一个自然数,各个数位上的数字之和是1997,则这个自然数最小是______.
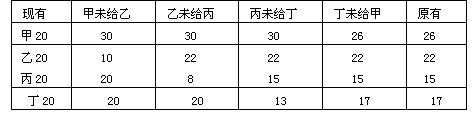
8.甲、乙、丙、丁四个学生共有80张卡片,甲给乙10张,乙给丙12张,丙给丁7张,丁给甲4张,这时四人手里的卡片数相等,则甲、乙、丙、丁原有卡片分别是______张.
![]()
个可约分数,□内的数最大是______.
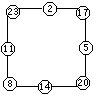
10.在8张小圆纸片上面分别写上2,5,8,11,14,17,20,23这8个数,把其中的四张分别放在一个大正方形的四个角上,再把余下的四张分别放在该正方形的四条边上,使得正方形每条边上的三个小圆纸片的数字之和都相等,那么这四个角上的四个数和最大是______.
二、解答题:
1.一艘轮船第一次顺流航行36千米,逆流航行12千米,共用12小时;第二次用同样的时间,顺流航行了12千米,逆流航行了20千米.求这艘轮船的静水速度及水流速度.
2.有甲、乙、丙三个人同时同向从同地出发,沿着周长为900米的环行跑道跑步,甲每分钟360米,乙每分钟300米,丙每分钟210米,问他们至少各绕了多少圈后才能再次相遇?
3.分母为1992的所有最简分数之和是多少?
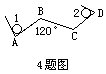
4.如图,一块半径为1厘米的圆板,从平面1的位置沿AB、BC、CD滚动到位置2.如果AB=BC=CD=10厘米,那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面2位数字)
模拟试卷31
一、填空题:
![]()

2.240
因为20=1×20=2×10=2×2×5=4×5,由于所求自然数最小,有20个约数的自然数可能是:
219,29×3,24×3×5,24×33
显然最小的是24×3×5=240.
3.19.4
![]()
![]()
![]()
4.如图
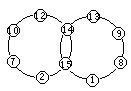
要使每个大圆圈上的六个数的和等于60,两个圆圈上的各数之和应为120,但已知给的10个数之和是91,120-91=29,29是两个大圆圈上公共的两个数之和,只有14+15=29,把这两个数添入大圆圈上公共小圆圈内,再把其它8个数分成和是31的两组.
5.六
因为一星期有7天,而7整除,1997÷3=665…2,说明还余下2个1997,由于
÷7=…3,3+3=6.
![]()
6.最低分至少9.44分,有8名裁判员.说有x名裁判员,最高分是a,最低分是b,则
9.72x=9.76(x-1)+b
9.72x=9.68(x-1)+a
即b=9.76-0.04x
a=0.04x+9. 68
所以a+b=9.76+9.68=19.44
由于a≤10,则b≥9.44,故最低分至少是9.44分.
由9.44=9.76-0.04x
x=8
![]()
要使这个自然数最小,则这个自然数的位数要尽可能少,这就要求各位数位上的数字尽可能大,最大取9.
1997÷9=221…8
![]()
8.甲26,乙22,丙15,丁17.
这类问题可以倒着想,最后这四人手里的卡片数相等,所以每人有卡片:
80÷4=20(张)
通过逆推法可以得出这四人原有的卡片数,列表如下:
9.98
由于要求原分数可约,必然原分数的倒数也可约.因为![]()
□+7必有因数 5或17.又因为□是一个两位数,而105= 5×21,含有因数5,所以□=105-7=98,即□中最大的两位数是98.
10.68,如图
题目要求正方形每条边上的三张小圆纸片的和都相等,其中四个角上的数在计算时重复计算各一次,因此四条边共12个数相加的和必是4的倍数,而8张小圆纸片上的数字之和为:
![]()
100是4的倍数,所以放在四个角上的数字必是4的倍数.由于
14+17+20+23=74
74不是4的倍数.但比74小的数72是4的倍数,但卡片中任意四个数的和都不等于72,依次考虑68,其中23、20、17、8这4个数的和正好是68,这样可以算出每条边上三个数之和是:
(68+100)÷4=42
根据这个结果很容易得出四个角上放置的数字,如图,通过计算检验得到正方形边上的四个数字,由此可见四个角上的四个数的和最大是68.
二、解答题:
1.船速是6千米/时,水速是2千米/时.
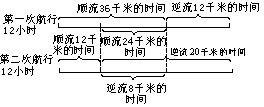
根据线段图可以看出,顺流36-12=24千米所用时间等于逆流20-12=8千米所用时间,即相同时间里顺流行了24千米,逆流行了8千米,所以顺流速度是逆流速度的
(36-12)÷(20-12)=3倍,假设第一次航行全是顺水航行:
顺水速度:(36+12×3)÷12=6(千米/时)
逆水速度:12÷(12-36÷6)=2(千米/时)
船速:(6+2)÷2=4(千米/时)
水速:(6-2)÷2=2(千米/时)
2.甲、乙、丙分别跑了12、10、7圈.
设x分钟之后三人相遇,相遇时,甲与乙的路程差应是900的倍数,即
(360-300)x=900m(m是自然数)
同理(300-210)x=900n(n是自然数)
(360-210)x=900p(p是自然数)
得x=15m,x=10n,x=6p.可知x是15、10、6的最小公倍数,有x=[15,10,6]=30,所以30分后甲、乙、丙三个人相遇,此时甲、乙、丙分别跑的圈数是:
360×30÷900=12(圈)
300×30÷900=10(圈)
210×30÷900=7(圈)
因为1992=3×8×83,因此分母为1992的最简分数的分子不能是2的倍数、3的倍数和83的
倍数.所以分母为1992,分子不是2或3的倍数
且小于1992的所有分数是:
![]()
这些数可以分成两类:一是分子被6除余1,二是分子被6除余5,即
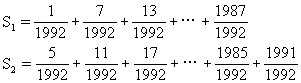
其中含有分子是83的倍数,这S1与S2的和减去这些倍数即为所求.
S1、S2的分子成等差数列,S1的分子为1、7、13、…、1987,共有(1987-1)÷6+1=332个数,S2的分子为5、11、17、…、1985、1991,共有(1991-5)÷6+1=332个数,所以
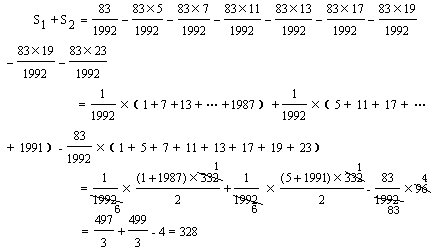
4.圆板滚过的图形面积是53.94平方厘米
解答本题的关键在于想象出圆板滚过的图形,现将圆板滚过的图形分割成a、b、c、d、e、f、g,其中图a、b、c分别是长为9厘米、8厘米、7厘米,宽是 2厘米的长方形;图 d、 f正好拼成一个圆;图e是
![]()
0.5厘米,厘米的小正方形与一个半径为0.5圆心角是90°的扇形面积之和.所以圆板滚过的图形面积为:
![]()
(平方厘米)