模拟试卷35
一、填空题:
![]()
![]()
3.有一条5.6米长的木料,如锯成每段长为0.8米的短木料,需要30分钟,那么锯成每段长为0.7米的短木料需要______分钟.
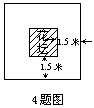
4.街心花园有一个正方形的花坛,四周有一条宽1.5米的甬道(如图),如果甬道的面积是27平方米,那么中间的花坛面积是______平方米.
5.按规律排列的一串数:1,2,4,7,11,16,22,29,…,这串数的第1997个数是______.
6.某学校四、五、六三个年级组织了一场文艺演出,共演出18个节目.如果每个年级至少演出四个节目,那么,这三个年级演出节目数的所有不同情况共有______种.
7.471除以一个两位数,余数是37,则这个两位数是______.
8.如果384×540×875×1875×( )的积的最后十个数字都是零,那么括号内填入的自然数最小是______.
9.将1,2,3,4,5,6,7这七个数分成两组,组成一个三位数和一个四位数,并使这两个数的乘积最大,那么这个三位数是______.
10.平面上有10个圆,最多能把平面分成______个部分.
二、解答题:
1.买语文书18本,数学书15本,共花167.1元,已知每本语文书比每本数学书贵0.3元,语文书、数学书每本各多少元?
2.小强期末五门考试的平均分数是87.5分,其中语文考了96分.如果小强语文只得了88分,那么他的平均成绩应是多少分?
3.甲、乙、丙三种大小不同的正方体木块,其中甲的棱长分别是乙、![]()
正方体,要求每种木块至少用一块,那么最少需要这三种木块多少块?
4.甲、乙两人在相距200米的直路上来回跑步,如果他们同时于6点05分分别在直路两端出发,当他们第11次相遇时,时间是6点19分,已知甲每秒比乙每秒多跑1米,问甲、乙两人的速度是每秒多少米?
模拟试卷35
一、填空题:
1.5.61
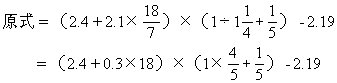
=(2.4+5.4)×1-2.19
=7.8-2.19
=5.61
![]()
3.35分
把5.6米长的木料锯成每段长为0.8米的短木料,恰好锯成7段,把5.6米长的木料锯成每段长为0.7米的短木料,恰好锯成8段.将一根木料锯成7段只需锯6次,锯6次用了30分,每次5分,即把这根木料锯成7段,需锯6次,每次所用时间是:
30÷(5.6÷0.8-1)=5(分)
锯成每段0.7米的短木料所需时间是:
5×(5.6÷0.7-1)=35(分)
4.9平方米
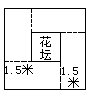
如图,将甬道分割成四个大小相等的长方形,每个长方形的面积是27÷4=6.75平方米,每个长方形的长是6.75÷1.5=4.5米,因此花坛的边长是4.5-1.5=3米,所以花坛的面积是3×3=9平方米.
5.
不妨设a1=1
a2=2=1+1
a3=4=2+2=1+1+2
a4=7=4+3=1+1+2+3
a5=11=7+4=1+1+2+3+4
……
a1997=1+1+2+3+4+…+1996
=1+(1+1996)×1996÷2
=1+1997×998
=1+
=
6.25
把18分成三个大于或等于4的整数的和,有以下几种分法:
18=4+4+10
=4+5+9
=4+6+8
=4+7+7
=5+6+7
=6+6+6
第一种分法有3种不同的情况;四年级演4个节目,五年级演4个节目,六年级演10个节目,简写成四4,五4,六10;或四4,五10,六4;或四10,五4,六4.同样,第四种分法也有3种不同的情况,第二、三、五种分法各有6种不同的情况,第六种分法只有一种情况,所以,这三个年级演出节目数的所有不同情况共有
3+6+6+3+6+1=25(种)
7.62
设所求两位数是a,则有a(471- 37),即a中434的约数,由于434=2×7×31,又a>37,所以这个两位数a=62.
8.50
积的末尾“0”的个数与因数中含有质因数2和5的个数有关,因此先将已知因数分解出质因数2和5,则有
384=2×2×2×2×2×2×2×3=27×3
540=2×2×5×27=22×5×27
875=5×5×5×7=53×7
1875=5×5×5×5×3=54×3
已知因数中共有9个质因数2,8个质因数5,由于积的末尾是十个零,所以还缺少1个2和2个5,故括号内填入的最小自然数是:
2×5×5=50
9.742
要使一个三位数和一个四位数的乘积最大,必然是把最大的数字放在因数的首位,那么7应该是三位数的首位还是四位数的首位呢?通过试验,7500×600=,6500×700=,知7在三位数的首位,6就是四位数的首位;然后考虑因数在十位上的数字,十位上的两个数字分别是3和4,那么比较乘积 6540×730与 6530×740的大小,根据“和相等的两个数,它们的差越小,则积越大”,而
6540+730=6530+740
且6530-740的差比6540-730的差小,所以6530×740的乘积大,由此可以确定三位数的十位数字是4.同样方法可以确定出三位数的个位数字是2,所以把1至7分成两组,这两组是6531和742,且它们的乘积最大,而742即为题目所求三位数.
一个圆把平面分成圆内和圆外两个部分;第二个圆同第一个圆相交,有两个交点,这样增加了两个部分,共有2+ 2= 4个部分;第三个圆与前两个圆都相交,而且不与其它的交点重合,第三个圆上有2×2= 4个交点,第三个圆被分成4段圆弧,也就是又增加了4个部分,三个圆把平面分成8个部分,依次类推,画第10个圆共有2×9= 18个交点,也就是增加了18个部分,因此平面内的10个圆把平面分成:
2+2×1+2×2+2×3+2×4+…+2×9=92(个)部分.
二、解答题:
1.语文书每本5.2元,数学书每本4.9元.
假设语文书与数学书的每本价格相同,那么语文书每本便宜0.3元,18本便宜0.3×18=5.4元,用总钱数167.1元减去5.4元的差恰好是18+15=33本数学书的价格,得数学书的单价是:
(167.1-0.3×18)÷(18+15)
=(167.1-5.4)÷33
=161.7÷33
=4.9(元)
4.9+0.3=5.2(元)……语文书的单价
另解:(167.1+ 0.3×15)÷(18+15)
=(167.1+ 4.5)÷33
=171.6÷33
=5.2(元)……语文书的单价
5.2-0.3=4.9(元)……数学书的单价
2.85.9分
小强语文从96分降到88分,实际上就是他的总分减少了96- 88= 8分,这8分使五科平均成绩下降了8÷5= 1.6分,所以小强的平均成绩是:
87.5-(96-88)÷5
=87.5-1.6
=85.9(分)
设甲的棱长为1,则乙的棱长为3,丙的棱长为4.显然大正方体的棱长不可能是5,否则无法同时放下乙、丙两种木块各1个,所以大正方体的棱长至少是7,也就是说大正方体的棱长为7时,它的体积最小.这样丙种木块只能用1块,而乙种木块最多用7块,为了使总的块数尽可能少,乙种木块用7块,剩下的用甲种木块去拼,共需要甲种木块:
7×7×7-4×4×4-7×3×3×3=90(块)
所以最少需要这三种木块:
90+1+7=98(块).
4.甲是每秒3米,乙是每秒2米.
甲、乙两人从出发到第11次相遇共用了14
分,即14×60= 840秒.除了甲、乙第1次相遇走了一个直路长200米,其余10次相遇均走了两个直路长200×2= 400米,因此840秒共走了:
200+200×2×10=4200(米)
这样得到甲、乙两人速度和是每秒走:
4200÷840=5(米)
又知甲与乙的速度差是每秒1米,由此得甲速度是每秒走:
(5+1)÷2=3(米)
乙每秒走:
(5-1)÷2=2(米).