重叠问题训练C卷

　　班级_______ 姓名_______ 得分_______

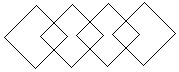
　　1.每边长是10厘米的正方形纸片，正中间挖了一个正方形的洞，成为一个边宽1厘米的方框，把4个这样的方框放在桌上，成为下图所示的图案。这些方框复盖住桌子的面积是多少平方厘米？

　　2.全班有50个人，其中爱好数学的有22人，爱好音乐的有22人，爱好体育的有22人，三样都爱好的有6人，都不爱好的有8人，问只爱一样的有几人？

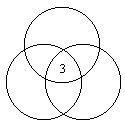
　　3.在图中，请在各圆互相分割的区域中填上1，2，4，5，6，7这六个数，使得每个圆圈里的四个数的和为15。

　　4.有50个女孩，她们的皮肤有白的或浅黑色的，眼睛则是蓝色的或褐色的，如果有14个蓝眼睛白肤色，31个是浅黑肤色，18个是褐色眼睛，那么褐色眼睛浅黑肤色的女孩有多少个？

　　5.国际象棋棋盘为8×8个正方形小格，能不能用15个凸字形纸片及一个田形纸片把棋盘完全覆盖？

　　6.有30分米长的木棍，现要在木棍上划线。先每隔2分米划一条线，再每隔3分米划一条线，最后按划线处锯开木棍，共能锯成多少段？

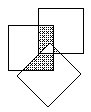
　　7.如图，在桌面上放置两两重叠，边长都一样的三个正方形纸片。已知盖住桌面的总面积是144平方厘米。三张纸片共同重叠部分的面积是42平方厘米，图中阴影面积为72平方厘米。求正方形的边长。

　　8.“六一”儿童节，某校有25个小朋友得奖，学校为他们准备了甲、乙、丙三种奖品让他们自由选择，有14人要甲种奖品，12人要乙种奖品，10人要丙种奖品，其中4人既要甲种又要乙种，但不要丙种奖品，2人既要甲种又要丙种，但不要乙种，只有1人三种都要。每个小朋友至少选择其中的一种，有几人要乙种和丙种而不要甲种？

　　9.试用若干个全等的任意四边形，来铺设地板，既不重叠，也不能有缝隙，应该怎样铺？

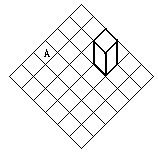
　　10.如图，在5×6的方格纸上放着一个小立方体，它每个面大小与方格大小相同，现在要翻转小立方体，使其走遍所有的方格，每个方格只能走一次，最后小立方体落到方格A内。问有可能吗？

　　11.一个长、宽、高分别为21、15、12（厘米）的长方体。现在从它的上面尽可能大的切下一个正方体。然后从剩余部分再尽可能大的切下一个正方体。最后再从第二次剩余的部分尽可能大的切下一个正方体，求剩下的体积。

　　12.将七个面积值为1的圆纸片放在桌面上，它们所盖住的总面积值等于

　　13.有A、B、C、D四个圆，它们的半径分别为1995厘米、1990厘米、1895厘米和1890厘米。问圆A和圆D两个面积和大，还是圆B与圆C两个圆的面积和大？

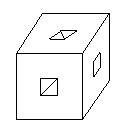
　　14.在一个棱长为5厘米的正方体木块的各个面中间打一个边长为1厘米的方孔（如图所示）后，这木块的体积是多少立方厘米？