| 1997小学数学奥林匹克试题 | |||
| 预赛(A)卷 | |||
| 1．计算：111111×999999+999999×777777=_________。 2．比较分数 3．用一台天平和重1克、3克、9克的砝码各一个，可称量不同的重量有_________种。
5．右面算式中不同字母表示不同的数字，相同字母表示相同的数字，那么被除数是_____。 7．上、下两册书的页码共有687个数字，且上册比下册多5页，则上册书有_________页。
9．设正方形的面积为1，右图中E、F分别为AB、AD 的中点， 10．某公司彩电按原价格销售，每台获利润60元；现在降价销售，结果彩电销售量增加了一倍，获得的总利润增加了0.5倍，则每台彩电降价_________元。 11．一件工程，甲队独做12天可以完成，甲队做3天后乙队做2天恰可完成一半，现在甲、乙两队合作若干天后，由乙队单独完成，做完后发现两段所用时间相等，则共用_________天。 12．电话费均以整分为单位计时收费（不足1分钟按1分钟计算）。市内电话三分钟内一律收费0.30元，超过三分钟则为0.30元/分,夜间21:00后对折收费。市外电话计费正好是市内的3倍，夜间21:00后也对折收费，但超过5分钟，就另加0.10元/分的附加费，超过10分钟，则另加0.20元/分的附加费，依此类推（附加费不对折）。 预赛（B）卷 1．计算：（精确到小数点后第三位） 2．计算： 3．甲、乙、丙三人去买书，乙买的书比甲买的书的本数的 4．一个四位数的数码都是由非零的偶数码组成，它又恰是某个偶数码组成的数的平方，则这个四位数是_______。
7．同预赛（A）卷第5题。 8．两个杯中分别装有浓度40％与10％的食盐水，倒在一起后混合食盐水浓度为30％。若再加入300克20％的食盐水，则浓度变成25％。那么原有40％的食盐水_________克 。 9．王春、陈刚、殷华当中有一人做了件坏事，李老师在了解情况中，他们三人分别说了下面几句话： 10．甲、乙两车分别从A、B两地出发，相向而行。出发时，甲、乙的速度比是5：4，相遇后，甲的速度减少20%，乙的速度增加20%，这样，当甲到达B地时，乙离A地还有10千米。那么A、B两地相距_________千米。 11．小李和小张同时开始制作同一种零件，每人每分钟能制作1个零件，但小李每制作3个零件要休息1分钟，小张每制作4个零件要休息1.5分钟。现在他们要共同完成制作300个零件的任务，需要_________分钟。 12．同预赛（A）卷12题。 预赛（C）卷 1． 2．1×1+2×2+3×3+…+1997×1997所得结果的个位数字是_______。 3．在1997后面补上三个数字，组成一个七位数1997□□□，如果这七位数能被4、5、6整除，那么补上的三个数字的和的最小可能值是_________。 4．将自然数1、10、19、28、37、46、55分别填入左下图中的七个框中，使每条直线上的三数之和与每个圆周上的三数之和都相等。那么圆心上的那个数应该填_________。 5．如右上图所示，在一个大正方形中，有两个带阴影的小正方形。较小的一个带阴影的小正方形的面积与较大的一个带阴影的小正方形的面积的比是_________。 6．在300到400之间的自然数之中，恰有3个约数的数的总和等于_________。 7．一个分数约分后将是 8．一件衣服，第一天按原价出售，没人来买；第二天降价20％出售，仍没人来买；第三天再降价24元，终于售出。已知售出价格恰是原价的56％，那么原价是_________元。 9．给定1997个连续的自然数。已知其中最小数与最大数的平均值是1997，那么最大数等于_________。 10．同预赛（B）卷第11题。 11．同预赛（B）卷第10题。 12．在甲、乙、丙三缸酒精溶液中，纯酒精的含量分别占48％、62.5％和 决赛（A）卷 1．计算：×-×=_________。 2． 3．下式中的“香港”、“中国”均代表一个两位自然数，那么香港=_________，中国=_________。 4．在下式的方框里分别填上2、4、6、8四个数字，使等式成立。最多可写出_________个不同的算式。
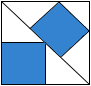
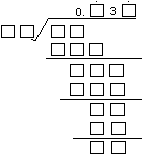
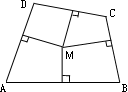
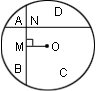
5．右面的除法算式中，只知道一个数字“3”，且商是一个循环小数，则被除数是_________。 6．有34个偶数的平均数，如果保留一位小数，得数是15.9，如果保留二位小数，得数最小是_________。 7．如左下图，四边形ABCD的周长是60厘米，点M到各边的距离都是4.5厘米，这个四边形的面积是_____平方厘米。 8．如右下图，在半径为4厘米的圆中有两条互相垂直的线段，把圆分成A、B、C、D四块。圆心O落在C中，O到M的距离为1厘米，M点到N点的距离为2厘米，那么A+C和B+D相比较，_________面积大，大_________平方厘米。 9．1997的数字之和是1+9+9+7=26，请你写出小于2000的四位数中，数字之和为26的除1997以外的所有数_____。 10．已知两个不同的单位分数之和是 11．有一些小朋友排成一行，从左面第一人开始每隔2人发一个苹果；从右面第一人开始每隔4人发一个桔子，结果有10个小朋友苹果和桔子都拿到。那么这些小朋友最多有_________人。 12．从电车总站每隔一定时间开出一辆电车。甲和乙两人在一条街上沿着同一方向步行，甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车。则电车总站每隔____分钟开出一辆电车。 决赛（B）卷 1．计算：++971997+71997+1997+997+97+7=_________。 2．计算：
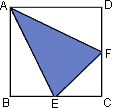
4．如右图，ABCD是正方形，E是BC边的中点，三角形ECF与三角形ADF面积一样大，那么三角形AEF（阴影部分）的面积是正方形ABCD面积的百分之______。（结果保留小数点后两位） 5．同决赛（A）卷第5题。 6．巧克力每盒9块，软糖每盒11块。要把这两种糖分发给一些小朋友，每样糖每人一块。由于又来了一位小朋友，软糖就要增加一盒，两种糖发的盒数就一样多。现在又来了一位小朋友，巧克力还要增加一盒。则最后共有小朋友_________人。 7．前五次考试的总分是428分，第六次至第九次的平均分比前五次平均分多1.4分。现在要进行第十次考试，要使后五次平均分高于所有十次的平均分，那么第十次至少要考_________分。（注：每次考试的分数都是整数） 8．有47位小朋友，老师要给每人发一支红笔和一支蓝笔。商店中每种笔都是5支一包或3支一包，不能打开包零售。5支一包的红笔61元、蓝笔70元，3支一包的红笔40元、蓝笔47元。则老师买所需的笔最少要花_________。 9．有一批工人进行某项工程，如果能调来8个人，10天就能完成；如果能调来3个人，就要20天才能完成。现在只能调来2个人，那么完成这项工程需要_________天。 10．将1至9九个数字写在一条纸带上，如下图：
将它剪成三段，每段上数字联在一起算一个数，把这三个数相加，使和能被77整除，那么中间一段的数是____。 11．同决赛（A）卷第11题。 12．同决赛（A）卷第12题。 决赛（C）卷 1．同决赛（B）卷第2题。 2．同决赛（A）卷第1题。 3．同决赛（B）卷第3题。 4．同决赛（A）卷第3题。 5．右下图是一个400米的跑道，两头是两个半圆，每一个半圆的弧长是100米，中间是一个长方形，长为100米，那么两个半圆的面积之和与跑道所围成的面积之比是_________。
9．1997的数字之和是1+9+9+7=26，则小于2000的四位数中，数字之和为26的数除1997外还有_________个。 10．一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是_________立方厘米。 11．同决赛（B）卷第10题。 12．同决赛（A）卷第12题。 |
、
、
、
的大小。
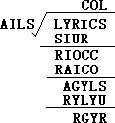4．六张卡片上分别标上1193、1258、1842、1866、1912、2494六个数，甲取3张，乙取2张，丙取1张，结果发现甲、乙各自手中卡片上的数之和一个人是另一个人的2倍，则丙手中卡片上的数是_________。
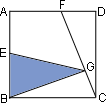8．学校一学期共安排86节数学课，单周一、三、五每天两节，双周二、四每天两节。开学第一周星期一开学典礼没上课，从星期三开始上，则最后一节数学课是星期_________上的。
，则阴影部分的面积为_________。
=_________。
=_________。
多3本，丙买的书比甲买的书的
少1本，则三人合计最少买_________本书。
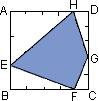5．六年级两班学生共109人，已知甲班男生占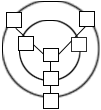
，乙班女生占
，则两班共有男生______人。
，
，则EFGH（阴影部分）的面积为_________。
=_________。 
，如果将这个分数的分子减少124，分母减少11，所得的新分数约分后将是
，那么原分数是_________。
。已知三缸酒精溶液总量是100千克，其中甲缸酒精溶液的量等于乙、丙两缸酒精溶液的总量。三缸溶液混合后，所含纯酒精的百分数将达56％。那么，丙缸中纯酒精的量是_________千克。
=_________。
，则这两个单位分数之差（较大分数为被减数）的最小值是_________。
=_________。
3．将0、1、2、3、4、5、6、7、8、9十个数字，组成三个三位数、一个一位数，并且使这四个数之和为999，我们要求最大的三位数尽可能小，则这个最大的三位数是_________。