2002小学奥林匹克数学决赛题

　　　　　　　　　　　　　　　  姓名　　　　 成绩

1.计算：(8.4×2.5＋9.7)÷(1.05÷1.5＋84÷2.8)＝（　　　）

2.计算：〔（5－4.25）×〕÷＋3.3÷=（　　　 ）

3.已知〔2＋（5.55×－÷□）〕÷0.913=10,则□=（　　）。

4．恰有两位数字相同的三位数共有（　　　 ）。

5．有两组数，第一组16个数的和是98，第二组的平均数是11，两组个所有数的平均数是8，则第二组有个（　　　 ）数。

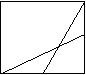6．如果一个三角形的底边长增加10％，底边上的高缩短10％，那么这个新三角形的面积是原来三角形面积的（　　　）％．　　　  D　　　　　 C

7．ABCD是边长为12厘米的正方形，E、F　　　　　　　　　　

分别是AB、BC边的中点，AF与CE交于G，则 　　　　　　 G　　F　　

四边形AGCD的面积＝（　　　）平方厘米。　　　　　　　　

8．在一圆形跑道上，甲从A点、乙从B点同时出发　　 A　　E　　 B

反向而行，8分钟后两人相遇，再过6分钟甲到B点，又过10分钟两人再次相遇，甲环行一周需（　　　 ）分钟．

9．甲工程队每工作6天休息一天，乙工程队每工作5天休息两天．一件工程，甲队单独做需经97天，乙队单独做需经75天．如果两队合作，从2002年3月3日开工，（　　 ）月（　  ）日可完工。

l0．用自然数n去除63，91，129得到的三个余数之和为25，那么n=（　  ）。

11．甲、乙、丙三人到图书馆去借书，甲每6天去一次，乙每8天去一次，丙每9天去一次，如果3月5日他们三人在图书馆相遇，那么下一次都到图书馆是（　 ）月（　 ）日。

12．有四个互不相同的自然数，最大的数与最小的数之差是4，最大数与最小数之积是奇数，而这四个数的和是最小的两位奇数，则这四个数的乘积是（　　　）。

13．圆周上均匀地放置了3l枚棋子，其中黑棋子14枚，白棋子17枚，若将圆周上任意两枚棋子交换位置称为一次对换，则最少经过（　　）次对换可使黑棋子在圆周上互不相邻．(两枚黑棋子之间至少有一枚白棋子)

14．两辆同一型号的汽车从同一地点同时出发，沿同一方向同速直线前进，每车最多能带20桶汽油(连同油箱内的油)．每桶汽油可以使一辆汽车前进50千米，车都必须返回出发地点，两车均可以借对方的油．为了使一辆车尽可能地远离出发点，另一辆车应该在离出发点（　　）千米的地方返回．