| 预赛(C)卷 1.计算:75×4.67+17.9×2.5=_________。 2.计算: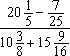 =_________。 =_________。 3.找出1992所有的不同质因数,它们的和是________。 4.比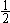 大,比5小,分母是13的最简分数有________个。 大,比5小,分母是13的最简分数有________个。 5.把一个正方形的一边减少20%,另一边增加2米,得到一个长方形,它与原来的正方形面积相等。那么,正方形的面积是________平方米。 6.有甲、乙两个数,如果把甲数的小数点向左移两位,就是乙数的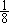 。那么,甲数就是乙数的________倍。 。那么,甲数就是乙数的________倍。 | 7.右图是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点。请你在图上选7个格点,要求其中任意三点都不在一条直线上,且使这7个点用直线连接后所围成的面积尽可能大,那么,所围成图形面积是________平方厘米。 | | 8.一个小于200的自然数,它的每位数字都是奇数,且它是两个两位数的乘积,那么,这个自然数是________。 9.在一条公路上,甲、乙两个地点相距600米。张明每小时行走4千米,李强每小时5千米。8点整,他们两人从甲、乙两地同时出发相向而行,1分钟后他们都调头反向而行,再过3分钟,他们又掉头相向而行,依次按照1,3,5,7,…(连续奇数)分钟数掉头行走,那么,张、李两人相遇时是8点________分。 10.有一堆糖果,其中,奶糖占45%。再放入16块水果糖后,奶糖就只占25%。那么,这堆糖中有奶糖________块。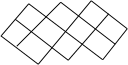 11.10个连续的自然数,上题的答数是其中第三大的数。把这10个数填到右图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等。那么,这个和数最小是________。 12.如果一个整数,与1,2,3这三个数,通过加减乘除运算(可以添括号)组成算式,结果等于上题答数,那么这个整数就称为可用的。那么,在4,5,6,7,8,9,10这七个数中,可用的数有________个。 预赛(B)卷 1.计算:75×4.67+17.9×2.5=________。 2.把一个正方形的一边缩短20%,另一边增加2米,得到一个长方形,它与原来正方形的面积相等。那么,正方形的面积是________平方米。 3.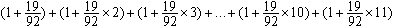 的结果是X。那么,与X最接近的整数是________。 的结果是X。那么,与X最接近的整数是________。 4.如果六位数1992□□能被95整除,那么它的最后两位数是________。 5.如果一个整数,与1,2,3这三个数,通过加减乘除运算(可以添括号)组成算式,使结果等于24,那么,这个整数就称为可用的。在4,5,6,7,8,9,10,11,12这九个数中,可用的数有________个。 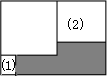 6.如图,长方形的面积是小于100 的整数,它的内部有三个边长是整数的正方形,正方形(2)的边长是长方形长的 6.如图,长方形的面积是小于100 的整数,它的内部有三个边长是整数的正方形,正方形(2)的边长是长方形长的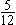 ,正方形(1)的边长是长方形宽的 ,正方形(1)的边长是长方形宽的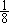 。那么,图中阴影部分的面积是________。 。那么,图中阴影部分的面积是________。
7.有一类小于200的自然数,每个数的各位数字之和是奇数,而且都是两个两位数的乘积(例如:144=12×12)。那么这一类自然数中,第三大的数是________。 8.一批工人到甲、乙两个工地进行清理工作,甲工地的工作量是乙工地的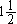 倍。上午去甲工地的人数是去乙工地的3倍;下午这批工人中的 倍。上午去甲工地的人数是去乙工地的3倍;下午这批工人中的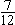 去甲工地,其他工人到乙工地。到傍晚时,甲工地的工作已做完,乙工地的工作还需4名工人再做1天。那么,这批工人有________人。 去甲工地,其他工人到乙工地。到傍晚时,甲工地的工作已做完,乙工地的工作还需4名工人再做1天。那么,这批工人有________人。  9.在400米跑道上,A、B两点相距100米(如图)。甲、乙两人分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑5米,乙每秒跑4米,每人每跑100米,都要停10秒钟。那么,甲追上乙需要的时间是________秒。 9.在400米跑道上,A、B两点相距100米(如图)。甲、乙两人分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑5米,乙每秒跑4米,每人每跑100米,都要停10秒钟。那么,甲追上乙需要的时间是________秒。
10.有一堆糖果,其中,奶糖占45%。再放入16块水果糖后,奶糖就只占25%。那么,这堆糖中有奶糖________块。  11.10个连续的自然数,上题的答数是其中第三大的数。把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等。那么,这个和数最小是________。 11.10个连续的自然数,上题的答数是其中第三大的数。把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等。那么,这个和数最小是________。
12.在一个停车场上,现有的车辆数,恰好是上题的答数,其中汽车是4个轮子,摩托车是3个轮子,这些车共有86个轮子。那么三轮摩托车有________辆。 预赛(A)卷 1.计算:4.25×5.24×1.52×2.51=________。 2.计算: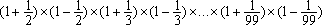 =________. =________. 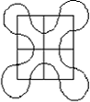 3.有八个半径为1毫米的小圆,用它们圆周的一部分连成一个花瓣图形(如图),图中黑点是这些圆的圆心。如果圆周率π=3.1416,那么花瓣圆形的面积是________平方厘米 3.有八个半径为1毫米的小圆,用它们圆周的一部分连成一个花瓣图形(如图),图中黑点是这些圆的圆心。如果圆周率π=3.1416,那么花瓣圆形的面积是________平方厘米
4.如果六位数1992□□能被105整除,那么它的最后两位数是________。 5.如图,长方形的面积是小于100 的整数,它的内部有三个边长是整数的正方形,正方形(2)的边长是长方形长的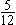 ,正方形(1)的边长是长方形宽的 ,正方形(1)的边长是长方形宽的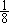 。那么,图中阴影部分的面积是________。 。那么,图中阴影部分的面积是________。  6.比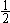 大,比7小,分母是6的最简分数有________个。 大,比7小,分母是6的最简分数有________个。 7.有一类小于200的自然数,每个数的各位数字之和是奇数,而且都是两个两位数的乘积(例如:144=12×12)。那么这一类自然数中,第三大的数是________。 8.一批工人到甲、乙两个工地进行清理工作,甲工地的工作量是乙工地的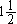 倍。上午去甲工地的人数是去乙工地的3倍;下午这批工人中的 倍。上午去甲工地的人数是去乙工地的3倍;下午这批工人中的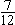 去甲工地,其他工人到乙工地。到傍晚时,甲工地的工作已做完,乙工地的工作还需4名工人再做1天。那么,这批工人有________人。 去甲工地,其他工人到乙工地。到傍晚时,甲工地的工作已做完,乙工地的工作还需4名工人再做1天。那么,这批工人有________人。 9一个圆的周长为1.26米,两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行。这两只蚂蚁每秒分别爬行1秒、3秒、5秒……(连续奇数),就掉头爬行。那么,它们相遇时,已爬行的时间是________秒。 10.有一堆糖果,其中,奶糖占45%。再放入16块水果糖后,奶糖就只占25%。那么,这堆糖中有奶糖________块。  11.10个连续的自然数,上题的答数是其中第三大的数。把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等。那么,这个和数最小是________。 11.10个连续的自然数,上题的答数是其中第三大的数。把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等。那么,这个和数最小是________。
12.某种考试已举行的次数恰好是上题的答数,共出了426题。每次出题数有25题,或16题,或20题。那么,其中考25道题的有________次。 决 赛 1.计算: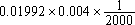 =________。 =________。 2.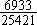 的最简分数是________。 的最简分数是________。 3.在下图的七个圆圈内各填一个数,要求每一条直线上的三个数中,当中的数是两边两个数的平均数。现在已经填好两个数,那么x=________。 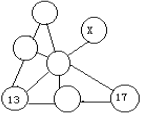 4.有八个数,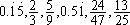 是其中的六个。如果按从小到大顺序排列时,第四个数是 是其中的六个。如果按从小到大顺序排列时,第四个数是 ,那么从大到小排列时,第四个数是________。 ,那么从大到小排列时,第四个数是________。 5.一个整数乘以13后,乘积的最后三位数是123,那么这样的整数中最小的是________。 6.把26,33,34,35,63,85,91,143分成若干组,要求每一组中任意两个数的最大约数是1,那么至少要分成________组。 7.在下面四个算式中,最大的得数应是________。 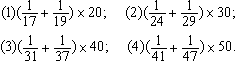 8.号码分别为101,126,173,193的四名运动员进行乒乓球比赛,规定每两人比赛的盘数是他们号码的和被3除所得的余数。那么,打球盘数最多的运动员打了________盘。  9.一个正方形(如图),被分成四个长方形,它们的面积分别是 9.一个正方形(如图),被分成四个长方形,它们的面积分别是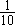 平方米、 平方米、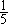 平方米、 平方米、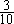 平方米和 平方米和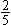 平方米.图中的阴影部分是一个正方形,那么阴影部分的面积是________平方米。 平方米.图中的阴影部分是一个正方形,那么阴影部分的面积是________平方米。
10.A、B、C、D、E五人在一次满分为100分的考试中,得分都是大于91的整数.如果A、B、C的平均分为95分,B、C、D的平均分为94分;A是第一名;E是第三名得96分,那么D的得分是________。 11.学校早晨6:00开门,晚上6:40关门.下午有一同学问老师现在的时间,老师说:从开校门到现在时间的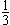 ,加上现在到关校门时间的 ,加上现在到关校门时间的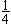 ,就是现在的时间,那么现在的时间是下午________。 ,就是现在的时间,那么现在的时间是下午________。 12.一辆汽车从甲地开往乙地。如果把车速提高20%,可以比原定时间提前一小时到达;如果以原速行使120千米后,再将速度提高25%,则可提前40分钟到达。那么,甲、乙两地相距________千米。 |