乘法原理

　　1 如右图，从甲地到乙地有2条路，从乙地到丙地有4条路，从甲地到丁地有3条路，从丁地到丙地也有3条路。问：从甲地到丙地共有多少种不同的走法？

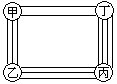
　　2 在下列各图中，一只甲虫要从A点沿着线段爬到B点，要求任何点不得重复经过。问：这只甲虫最多各有几种不同走法？

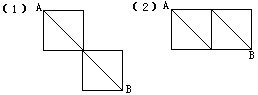
　　3 题库中有三种类型的题目，数量分别为30道、40道和45道，每次考试要从三种类型的题目中各取一道组成一张试卷。问：由该题库共可组成多少种不同的试卷？

　　4 在下面一排数字中间的任意两个位置写上两个“＋”号，可以得到三个自然数相加的加法算式，所有可以这样得到的不同的加法算式共有多少个？

　　1 2 3 4 5 6 7 8 9

　　5 一个三位数，如果它的每一位数字都不小于另一个三位数对应数位上的数字，就称它“吃掉”另一个三位数。例如，532吃掉311，123吃掉123。但726与267相互都不被吃掉。问：能吃掉678的三位数共有多少个？

　　6 用数字0，1，2，3，4可以组成多少个不同的三位数（数字允许重复）？

　　7 用数码 0～ 7可以组成多少个小于1000的自然数（数码可以重复使用）？

　　8 要从五年级六个班中评选出学习、体育、卫生先进集体各一个，有多少种不同的评选结果？

　　9 在自然数中，用两位数做被减数，一位数做减数，共能组成多少个不同的减法算式？

　　10 书架上有8本不同的画报和10本不同的书，每次只能从书架上任意取一本画报和一本书，共有多少种不同的取法？

　　11 甲、乙二人准备在一个6×6的方格纸（右图）上各放一枚棋子在方格中，要求两枚棋子不在同一行也不在同一列。问：共有多少种放法？

　　12 在左下图所示的方格纸中放黑棋子和白棋子各一枚，要求两枚棋子不在同一行也不在同一列。问：共有多少种放法？

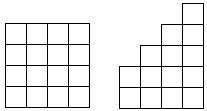
　　13 将4个棋子摆放到右上图的方格中，要求每一行、每一列最多摆一个棋子，共有多少种不同的摆法？

　　14 某短跑队有9名运动员，其中2人起跑技术好，另外有3人跑弯道技术好，还有2人冲刺技术好。现在要从中选4人组队参加 4×100米接力赛，为使每人充分发挥特长，共有多少种组队方式？（注： 4×100米接力赛中，第一棒起跑，第二棒跑直道，第三棒跑弯道，第四棒冲刺。）

　　15 用四种颜色对下列各图的A，B，C，D，E五个区域染色，要求相邻的区域染不同的颜色。问：各有多少种不同的染色方法？

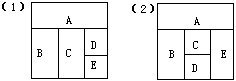
　　16 已知15120=2⁴×3³×5×7，问：15120共有多少个不同的约数？

　　17 在所有的四位数中，前两位的数字之和与后两位的数字之和都等于6的共有多少个？

　　18 在三位数中，至少出现一个6的偶数有多少个？

　　19 有三组数：（1）1，2，3；（2）0.5，1.5，2.5，3.5； （3）4，5，6。如果从每组数中各取出一个数相乘，那么所有不同取法的三个数乘积的总和是多少？

　　20 将 1332， 332， 32， 2这四个数的 10个数码一个一个地划掉，要求先划位数最多的数的最小数码。共有多少种不同的划法？

　　21 有10粒糖，每天至少吃一粒，吃完为止。共有多少种不同的吃法？